88-341 תשעג סמסטר א/תרגילים/תרגיל 8 הדרכה: הבדלים בין גרסאות בדף
(יצירת דף עם התוכן "== הדרכה נוספת לשאלה 2 == בסעיף א', מוצע לכם להוכיח את הרציפות בהחלט של <math>\sqrt{x}</math> ע"י הוכחת נ...") |
אין תקציר עריכה |
||
| שורה 19: | שורה 19: | ||
לגבי סעיף ב' - ניתן להוכיח את הרציפות בהחלט של <math>\begin{cases} x^2 \sin \frac{1}{x} & x \neq 0 \\ 0 & x=0 \end{cases}</math> ע"פ ההגדרה, אבל כדאי לתת למקרה שאחד הקטעים <math>(a_k,b_k)</math> מתחיל באפס התייחסות שונה. | לגבי סעיף ב' - ניתן להוכיח את הרציפות בהחלט של <math>\begin{cases} x^2 \sin \frac{1}{x} & x \neq 0 \\ 0 & x=0 \end{cases}</math> ע"פ ההגדרה, אבל כדאי לתת למקרה שאחד הקטעים <math>(a_k,b_k)</math> מתחיל באפס התייחסות שונה. | ||
'''רמז נוסף''': משפט הערך הממוצע של לגראנז'. | |||
גרסה אחרונה מ־15:29, 1 בינואר 2013
הדרכה נוספת לשאלה 2
בסעיף א', מוצע לכם להוכיח את הרציפות בהחלט של [math]\displaystyle{ \sqrt{x} }[/math] ע"י הוכחת נוסחת ניוטון לייבניץ: [math]\displaystyle{ \sqrt x -\sqrt 0=\int_0^x \frac{1}{2\sqrt t} \, dm(t) }[/math].
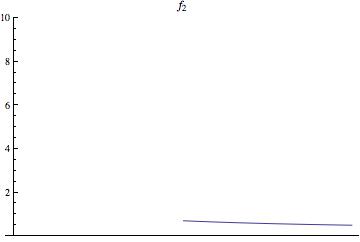
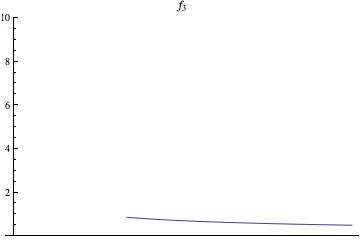
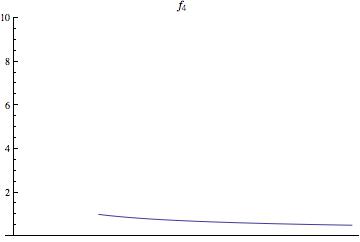
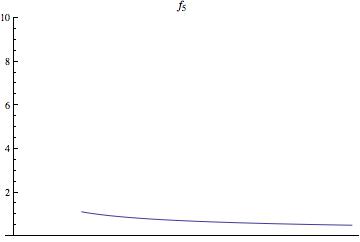
שימו לב שאסור להשתמש במשפט היסודי מתורת רימן, כי מדובר באינטגרל לא אמיתי (הפונקציה לא חסומה בסביבת [math]\displaystyle{ x=0 }[/math]), והמשפט המקשר בין אינטגרל רימן לאינטגרל לבג מההרצאה הוכח רק לאינטגרל הרגיל, של פונקציה חסומה על קטע סגור. דרך אחת להתגבר על הקושי היא להגדיר סדרה עולה של פונקציות [math]\displaystyle{ 0 \le f_1 \le f_2 \le \dots }[/math] מדידות (ראו גרפים להמחשה) ולהשתמש במשפט ההתכנסות המונוטונית)
נסו לרשום את הסדרה במונחים של פונקציות אינדיקטור.
לגבי סעיף ב' - ניתן להוכיח את הרציפות בהחלט של [math]\displaystyle{ \begin{cases} x^2 \sin \frac{1}{x} & x \neq 0 \\ 0 & x=0 \end{cases} }[/math] ע"פ ההגדרה, אבל כדאי לתת למקרה שאחד הקטעים [math]\displaystyle{ (a_k,b_k) }[/math] מתחיל באפס התייחסות שונה.
רמז נוסף: משפט הערך הממוצע של לגראנז'.