משתמש:אור שחף/133 - הרצאה/20.2.11: הבדלים בין גרסאות בדף

מתוך Math-Wiki
 
(17 גרסאות ביניים של 4 משתמשים אינן מוצגות)
שורה 1: שורה 1:
== אינטגרציה ==
{{כותרת נושא|אינטגרציה|נושא ראשון}}
'''הגדרה שגוייה:''' אינטגרל הוא לא השטח שמתחת לגרף. למעשה, השטח שמתחת לגרף מוגדר להיות תוצאת האינטגרל (כפי שאנחנו מכירים מהחומר לבגרות).
'''הערה:''' האינטגרל הוא '''לא''' שטח שמתחת לגרף. למעשה, השטח מתחת לגרף מוגדר לפי האינטגרל.
===דוגמת חישוב (ידני) של שטח שמתחת לגרף===
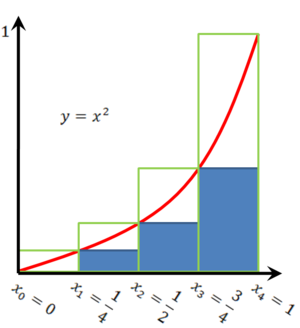
[[קובץ:השטח מתחת ל-x בריבוע לפי מלבנים.png|300px|ממוזער|ימין|הגרף של <math>y=x^2</math> והמלבנים החוסמים (עם גבול ירוק) והחסומים (בצבע כחול).]]
נתון הגרף של <math>y=x^2</math> ונרצה לחשב את השטח שמתחת לו בקטע <math>[0,1]</math>.
נחלק את הקטע:
{{left|<math>0=x_0<x_1<x_2<\dots<x_n=1</math>}}
כך שבאופן כללי <math>x_k=k/n</math> (בגרף מוצג המקרה הפרטי <math>n=4</math>).


דוגמת חישוב (ידני) של השטח:
מעל כל תת קטע <math>[x_{k-1},x_k]</math> נבנה "מלבן חוסם" שגובהו <math>\left({k\over n}\right)^2=x_k^2</math>. שטח כל המלבנים הללו הוא "שטח חוסם" {{left|<math>\overline S:=\sum_{k=1}^n\frac1n\left({k\over n}\right)^2=\frac1{n^3}\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6n^3}</math>}}


(1)
כמו כן, מעל כל תת קטע <math>[x_{k-1},x_k]</math> נבנה "מלבן חסום" שגובהו <math>\left({k-1\over n}\right)^2=x_{k-1}^2</math>. ביחד מלבנים אלה מהווים "שטח חסום" {{left|<math>\underline S:=\frac1n\sum_{k=1}^n\left({k-1\over n}\right)^2=\frac1{n^3}\sum_{k=1}^n(k-1)^2=\frac1{n^3}\sum_{k=1}^{n-1}k^2=\frac{(n-1)n(2n-1)}{6n^3}</math>}}


ברור שטחי המלבנים בוודאי גדול משטח הגרף (נתעלם כרגע מהעובדה שלא הגדרנו את האינטגרל ולכן השטח לא מוגדר).
כעת, אם A מציין את השטח שמתחת לגרף, בוודאי ש-<math>\underline S\le A\le\overline S</math>, ז"א <math>\frac{(n-1)(2n-1)}{6n^2}\le A\le\frac{(n+1)(2n+1)}{6n^2}</math>. הדבר נכון לכל <math>n\in\mathbb N</math> ולכן נוכל להשאיף את <math>n\to\infty</math> ולקבל
<math>\frac13\le A\le\frac13</math>, לכן <math>A=\frac13</math>. {{משל}}


נחלק את הקטע <math>[0,1]</math>:


<math>0=x_0<x_1<x_2<\dots<x_n=1</math>
----


<math>x_k=k/n</math>


מעל כל תת קטע קטן <math>[x_{k-1},x_k]</math>
'''הגדרה:''' תהי f מוגדרת בקטע I. נאמר שהפונקציה F קדומה ל-f ב-I אם <math>\forall x\in I:\ F'(x)=f(x)</math>.


נבנה "מלבן חוסם" שגובהו <math>\left({k\over n}\right)^2=x_k^2</math>. ביחד מלבנים אלו יוצרים שטח חוסם <math>
''דוגמה:'' אם <math>f(x)=x^2</math> אז <math>F(x)=\frac{x^3}3</math>.


==משפט 0==
אם F ו-G קדומות ל-f בקטע I אז קיים קבוע c כך ש-<math>F(x)=G(x)+c</math>


===הוכחה===
נגדיר <math>H(x)=F(x)-G(x)</math> ולכן <math>\forall x\in I:\ H'(x)=F'(x)-G'(x)=f(x)-f(x)=0</math>. מכאן ש-H היא פונקציה קבועה ולכן יש קבוע c כך ש-<math>F(x)-G(x)=H(x)=c\implies F(x)=G(x)+c</math>. {{משל}}


----


'''הגדרה אינטואיטיבית:''' תהי <math>f(x)\ge0</math> רציפה בקטע <math>[a,b]</math>. נסמן ב-<math>\int\limits_a^b f</math> את השטח שמתחת לגרף.


==המשפט היסודי של חשבון אינטגרלי {{הערה|(בצורה אינטואיטיבית)}}==
תהי <math>f(x)\ge0</math> מוגדרת ורציפה ב-<math>[a,b]</math>.
# לכל <math>x\in[a,b]</math> נגדיר <math>A(x)=\int\limits_a^x f</math> אזי <math>\forall x\in[a,b]:\ f(x)=A'(x)</math>.
# אם F קדומה ל-f ב-<math>[a,b]</math> אז <math>\int\limits_a^b f=F(b)-F(a)</math>.


line S=\sum_{k=1}^n\frac1n\left({k\over n}\right)^2=\frac1{n^3}\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6n^3}</math>
===הוכחה===
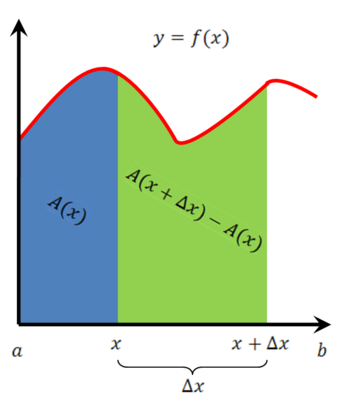
[[קובץ:הוכחה אינטואיטיבית למשפט היסודי של החשבון האינפיניטסימלי.png|ימין|ממוזער|350px]]
# יהי x נתון. לפי ההגדרה <math>A'(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x}</math>. בגרף: <math>=A(x+\Delta x)-A(x)</math> השטח של החלק הירוק ו-<math>=\Delta x</math> בסיס החלק הירוק. לפיכך <math>=\frac{A(x+\Delta x)-A(x)}{\Delta x}</math> הגובה הממוצע של הפונקציה בחלק הירוק. לכן <math>=A'(x)</math> הגובה הממוצע של החלק הירוק (כאשר <math>\Delta x\to0</math>) <math>f(x)=</math>. {{משל}}
# נתונה פונקציה קדומה F. מחלק 1 ידוע גם ש-A פונקציה קדומה (של f). לפי משפט 0 יש קבוע c כך ש-<math>F(x)=A(x)+c</math> ולכן <math>F(b)-F(a)=A(b)+c-(\underbrace{A(a)}_{=0}+c)=A(b)=\int\limits_a^b f</math>. {{משל}}


כמו כן, מעל כל קטע קטן <math>[x_{k-1},x_k]</math> נבנה "מלבן חסום" שגובהו <math>\left({k-1\over n}\right)^2=x_{k-1}^2</math> ביחד מלבנים אלה מהווים שטח חסום <math>\underline S=\frac1n\sum_{k=1}^n\left({k-1\over n}\right)^2=\frac1{n^3}\sum_{k=1}^n(k-1)^2=\frac1{n^3}\sum_{k=1}^{n-1}k^2=\frac{n(n+1)(2n+1)}{6n^3}</math>
=האינטגרל לפי דרבו=
==הקדמה - הגדרות==
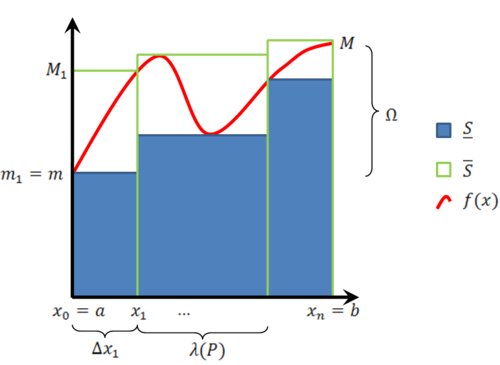
[[קובץ:הגדרת הערכים באינטגרל לפי דרבו.png|שמאל|500px|ממוזער]]
תהי f מוגדרת וחסומה ע"י <math>m:=\inf f</math> ו- <math>M:=\sup f</math> בקטע <math>[a,b]</math>. נגדיר את התנודה של f ע"י <math>\Omega:=M-m</math>. כעת נגדיר חלוקה P של <math>[a,b]</math> כקבוצה <math>\{x_0,x_1,\dots,x_n\}</math> המקיימת: <math>a=x_0<x_1<\dots<x_n=b</math>. עוד נגדיר לכל k את אורך תת קטע מספר k להיות <math>\Delta x_k:=x_k-x_{k-1}</math> ואת הפרמטר של P להיות <math>\lambda(P):=\max_{k=1}^n\Delta x_k</math>.


כעת אם A מציין את השטח שמתחת לגרף בוודאי ש-<math>\underline S\le A\le\overline S</math>.
לכל k כך ש-<math>1\le k\le n</math> נגדיר גם <math>M_k:=\sup\{f(x):\ x_{k-1}\le x\le x_k\}</math> וכן <math>m_k:=\inf\{f(x):\ x_{k-1}\le x\le x_k\}</math>. בהתאם לכך נגדיר:
* שטח חוסם - הסכום העליון: <math>\overline S(f,P):=\sum_{k=1}^n M_k\Delta x_k</math>
* שטח חסום - הסכום התחתון: <math>\underline S(f,P):=\sum_{k=1}^n m_k\Delta x_k</math>


(2)
==משפט 1==
בסימונים הנ"ל, עבור כל חלוקה P מתקיים <math>m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)</math>.


ז"א <math>\frac{n(n+1)(2n+1)}{6n^3}\le A\le\frac{n(n+1)(2n+1)}{6n^3}</math>.
===הוכחה===
הדבר נכון לכל <math>n\in\mathbb N</math>. לכן נוכל להשאיף <math>n\to\infty</math> לקבל
{|
<math>\frac13\le A\le\frac13</math> ולכן <math>A=\frac13</math>
{{=|l=m(b-a)
 
  |r=\sum_{k=1}^n m\Delta x_k
=== בניית האינטגרל לפי דרבו - אחר כך ===
  |c=<math>=\sum_{k=1}^n\Delta x_k</math> סכום כל הרווחים בין n נקודות החלוקה <math>b-a=</math>, לכן:
 
}}
'''הגדרה:''' תהי <math>f(x)</math> מוגדרת בקטע I. נאמר שהפונקציה <math>F(x)</math> קדומה ל-f ב-I אם <math>\forall x\in I:\ F'(x)=f(x)</math>.
{{=|r=\sum_{k=1}^n m_k\Delta x_k=\underline S(f,P)
  |o=\le
  |c=לכל k מתקיים <math>m\le m_k</math>.
}}
{{=|r=\sum_{k=1}^n M_k \Delta x_k=\overline S(f,P)
  |o=\le
}}
{{=|r=\sum_{k=1}^n M\Delta x_k
  |o=\le
}}
{{=|r=M(b-a)
}}
|}
{{משל}}


''דוגמה:''
נשים לב כי לפי משפט 1 המספרים <math>\overline S(f,P),\underline S(f,P)</math> חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).
...


'''משפט 0:''' אם <math>F(x)</math> ו-<math>G(x)</math> קדומות ל-<math>f(x)</math> בקטע I אז קיים קבוע c כך ש-<math>F(x)=G(x)+c</math>
לכן מוגדרים היטב ה"אינטגרל העליון" <math>\overline{\int}_a^b f:=\inf_P \overline S(f,P)</math> ו"האינטגרל התחתון" <math>\underline\int_a^b f:=\sup_P \underline S(f,P)</math>.


'''הוכחה:''' נגדיר <math>H(x)=F(x)-G(x)</math> לכן <math>H'(x)=F'(x)-G'(x)</math>
==הגדרת האינטגרל לפי דרבו==
תהי f מוגדרת וחסומה ב-<math>[a,b]</math>. נאמר ש-f אינטגרבילית לפי דרבו ב-<math>[a,b]</math> אם <math>\underline\int_a^b f=\overline{\int}_a^b f</math> ואם הם שווים אז נגדיר <math>\int\limits_a^b f</math> להיות הערך המשותף של <math>\underline\int f</math> ו-<math>\overline{\int} f</math>.


....
===דוגמה===
בקטע <math>[a,b]</math> כלשהו נגדיר את פונקצית דיריכלה <math>D(x)=\begin{cases}1&x\in\mathbb Q\\0&x\not\in\mathbb Q\end{cases}</math>.
נקח חלוקה כלשהי ל-<math>[a,b]</math>: <math>a=x_0<x_1<\dots<x_n=b</math>.


לפי תוצאה ממשפט לגראנג' <math>F(x)-G(x)=H(x)=c\implies F(x)=G(x)+c</math>
לכל k מתקיים <math>M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}=1</math> וכן <math>m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}=0</math>. לכן <math>\overline S(f,P)=\sum_{k=1}^n M_k\Delta x_k=\sum_{k=1}^n 1\Delta x_k=b-a</math> ואילו <math>\underline S(f,P)=\sum_{k=1}^n m_k\Delta x_k=\sum_{k=1}^n 0\Delta x_k=0</math>. מכאן <math>\underline\int_a^b f=\sup_P \underline S(f,P)=0</math> ו-<math>\overline{\int}_a^b f=\inf_P \overline S(f,P)=b-a</math>, וכייוון שאינם שווים f אינה אינטגרבילית. {{משל}}


{{משל}}


----
----
'''הגדרה:''' תהי <math>f(x)\ge0</math> רציפה בקטע <math>[a,b]</math>.
...


המשפט היסודי של חשבון אינטגרלי (בצורה אינטואיטיבית): תהי <math>f(x)\ge0</math> מוגדרת ורציפה ב-<math>[a,b]</math>. לכל <math>x\in[a,b]</math> נגדיר <math>A(x)=\int\limits_a^x f(t)dt</math> אזי <math>f(x)=A'(x)</math> לכל <math>x\in[a,b]</math>.


2) אם <math>F(x)</math> קדומה ל-<math>f(x)</math> ב-<math>[a,b]</math> אז <math>\int\limits_a^bf(t)dt=F(b)-F(a)</math>.
'''הגדרה:''' תהי P חלוקה של קטע <math>[a,b]</math>. חלוקה Q של <math>[a,b]</math> נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.


----
==משפט 2==
תהי f מוגדרת וחסומה ב-<math>[a,b]</math>, תהי P חלוקה של <math>[a,b]</math> ו-Q עידון של P ע"י הוספת r נקודות. אזי
{{left|
<math>0\le\overline S(f,P)-\overline S(f,Q)\le r\lambda(P)\Omega</math>


'''הוכחה:''' (א) (3)
<math>0\le\underline S(f,Q)-\underline S(f,P)\le r\lambda(P)\Omega</math>
רואים <math>A(a)=0</math>
}}
המטרה <math>A(b)=\int\limits_a^bf(t)dt</math>.
(נזכיר ש-<math>\lambda(P)=\max_{1\le k\le n}\Delta x_k</math> ו-<math>\Omega=\sup_{x\in[a,b]} f(x)-\inf_{x\in[a,b]} f(x)</math>)


<math>A(x)</math> עולה
כלומר, הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-<math>r\lambda(P)\Omega</math>.


כעת לפי ההגדרה <math>A'(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x}</math>
===הוכחה===
מקרה ראשון: <math>r=1</math>. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת <math>x_i'</math> כך ש-<math>x_{i-1}<x_i'<x_i</math> עבור i כלשהו. בהתאם לכך נגדיר <math>M_i^-:=\sup\{f(x):\ x_{i-1}\le x\le x_i'\}</math> ו-<math>M_i^+:=\sup\{f(x):\ x_i'\le x\le x_i\}</math>.
כמו כן, לא שינינו כל תת קטע <math>[x_{k-1},x_k]</math> עבור <math>k\not=i</math> כלשהו. לכן <math>\overline S(f,P)-\overline S(f,Q)=M_i\Delta x_i-\Big(M_i^-(x_i'-x_{i-1})+M_i^+(x_i-x_i')\Big)</math>


בציור <math>A(x+\Delta x)-A(x)</math> = השטח הארובה
לפי ההגדרות <math>M_i\ge M_i^+,M_i^-</math> ולפיכך {{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\ge M_i\Delta x_i-\Big(M_i(x_i'-x_{i-1})+M_i(x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i'-x_{i-1}+x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i-x_{i-1})\Big)\\&=0\end{align}</math>}}
<math>\Delta x</math> = בסיס הארובה
לכן <math>\frac{A(x+\Delta x)-A(x)}{\Delta x}</math> = הגובה הממוצע של הארובה.


כאשר <math>\Delta x\to0</math> זה שואף ל-<math>f(x)</math> שהיא <math>A(x)</math>.
{{המשך סיכום|תאריך=22.2.11}}


(ב) נתונה פונקציה קדומה <math>F(x)</math> אבל מחלק א ידוע שגם <math>A(x)</math> פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-<math>F(x)=A(x)+c</math>
כמו כן,
 
{{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\le M_i(x_i-x_{i-1})-m_i(x_i-x_{i-1})\\&=(M_i-m_i)(x_i-x_{i-1})\\&\le\Omega(x_i-x_{i-1})\\&\le\underbrace{r}_{=1}\lambda(P)\Omega\end{align}</math>}}
לכן <math>F(b)-F(a)=A(b)+c-\underbrace{(A(a)+c)}_{=0}=A(b)=\int\limits_a^bf(x)dx</math>
 
=== הגישה של דרבו ===
תהי <math>f(x)</math> מוגדרת וחסומה <math>m\le F(x)\le M</math> בקטע <math>[a,b]</math>. נגדיר את התנודה של f ע"י <math>\Omega=M-m</math>. כעת נגדיר חלוקה P של <math>[a,b]</math>
 
<math>a=x_0<x_1<\dots<x_n=b</math>
 
 
עוד נגדיר לכל <math>k</math> אורך תת קטע מספר k = <math>\Delta x_k=x_k-x_{k-1}</math>
 
והפרמטר של P, <math>\lambda(P)</math> מוגדר ע"י <math>\lambda(P)=\max_{1\le k\le n}\Delta x_k</math>
 
לכל k, <math>1\le k\le n</math> נגדיר
<math>M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}</math> וכן <math>m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}</math>.
 
(4)
 
בהתאם לכך נגדיר "שטח חוסם"
0הסכום העליון
<math>\overline S(f,P)=\sum_{k=1}^n m_k\Delta x_k</math>
ושטח חסום תחתון
<math>\underline S(A,P)=\sum_{k=1}^n m_k\Delta x_k</math>
 
 
<math>\overline S(f,P)=\sum_{k=1}^nm_k\Delta x_k</math>
 
משפט 1: עבור כל חלוקה P
 
<math>m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)</math>
 
הוכחה: <math>m(b-a)=m\sum_{k=1}^n\Delta x_k</math> (כי <math>\sum_{k=1}^n\Delta x_k</math> = סכום כל הרווחים בין n נקודות החלוקה = b-a)
 
<math>=\sum_{k=1}^n m\Delta x_k\le \sum_{k=1}^n m_k\Delta x_k</math> (כי לכל k מתקיים <math>m\le m_k</math>)
 
<math>=\underline S(f,P)\le\sum_{k=1}^n M_k \Delta x_k=\overline S(f,P)\le\sum_{k=1}^n M\Delta x_k=M\sum_{k=1}^n \Delta x_k=M(b-a)</math>
 
לפי משפט 1 המספרים <math>\overline S(f,P),\underline S(f,P)</math> חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).
 
לכן מוגדרים היטב ה"אינטגרל העליון" <math>\overline\int\limits_a^b f(x)dx=\inf_P \overline S(f,P)</math>  ו"האינטגרל התחתון" <math>\underline\int\limits_a^b f(x)dx=\sup_P \underline S(f,P)</math>.
 
=== הגדרת האינטגרל לפי דרבו ===
תהי f(x) מוגדרת וחסומה ב-<math>[a,b]</math> נאמר ש-f אינטגרבילית (דרבו) ב-<math>[a,b]</math> אם <math>\underline\int\limits_a^b f(x)dx=\overline\int\limits_a^b f(x)dx</math> ואם הם שווים אז נגדיר <math>\int\limits_a^b f(x)dx</math> להיות הערך המשותף של <math>\underline\int f</math> ו-<math>\overline\int f</math>.
----
דוגמהף בקטע <math>[a,b]</math> כלהו נגדיר את פונקצית דיריכלה <math>f(x)=\begin{cases}q\quad x\in\mathbb Q\\0\quad x\not\in\mathbb Q\end{cases}</math>.
נקח חלוקה כלשהי ל-<math>[a,b]</math>
 
<math>a=x_0<x_1<\dots<x_n=b</math> לכל k
 
<math>M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}=1</math> וכן <math>m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}=0</math>
 
לכן <math>\overline S(f,P)=\sum_{k=1}^n M_k\Delta x_k=\sum_{k=1)^n 1\Delta x_k=b-a</math>
 
ואילו <math>\underline S(f,P)=\sum_{k=1}^n m_k\Delta x_k=\sum_{k=1)^n 0\Delta x_k=0</math>.
 
מכאן <math>\underline\int\limits_a^b f(x)dx=\sup_P \underline S(f,P)=0</math> ו-<math>\overline\int\limits_a^b f(x)dx=\inf_P \overline S(f,P)=b-a</math>. הם לא שווים ולכן f לא אינטגרבילית.
 
הגדרה: תהי P חלוקה של קטע <math>[a,b]</math>. חלוקה Q של <math>[a,b]</math> נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.
 
משפט 2: תהי <math>f(x)</math> מוגדרת וחסומה ב-<math>[a,b]</math>. תהי P חלוקה של <math>[a,b]</math> ו-Q עידון של P ע"י הוספת r נקודות. אז
 
<math>0\le\overline S(f,P)-\overline S(f,Q)\le r\lambda(P)\Omega</math>
<math>0\le\underline S(f,P)-\underline S(f,Q)\le r\lambda(P)\Omega</math>


(כאשר <math>\lambda(P)=\max_{1\le k\le n}\Delta x_k</math> ו-<math>\Omega=\sup\{f(x)\}-\inf\{f(x)\}</math>)
מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר <math>\Omega\lambda(P)</math> בכל אחת מ-r המפעמים. לכן מיד נסיק <math>0\le\overline S(f,P)-\overline S(f,Q)\le r\Omega\lambda(P)</math>.


ז"א הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-<math>\lambda(P)</math>
ההוכחה לסכום תחתון דומה. {{משל}}


הוכחה: מקרה ראשון: <math>r=1</math>. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת <math>x_i'</math>. כך ש-<math>x_{i-1}<x_i'<x_i</math>. בהתאם לכך נגדיר <math>M_i'=\sup\{f(x):\ x_{i-1}\le x\le x_i\}</math> ו-<math>M_i''=\sup\{f(x):\ x_i'\le x\le x_i\}</math>
===מסקנה 1===
כעת בכל תת קטע <math>[x_{k-1},x_k]</math> מתקיים <math>k\not=i</math>. לא שינינו כלום.
נקח f כנ"ל ונניח ש-P ו-Q הן שתי חלוקות כלשהן של <math>[a,b]</math>. אזי <math>\underline S(f,P)\le\overline S(f,Q)</math>.
לכן <math>\overline S(f,P)-\overline S(f,Q)=\underbrace{M_Delta x_i}_{(1)}-\underbrace{(M_i'(x_i'-x_{i-1})+M_i''(x_i-x_i'))}_{(2)}</math>
====הוכחה====
# תרומת קטע i ל-<math>\overline S(f,P)</math>
נבנה עידון משותף, ז"א <math>R=P\cup Q</math>. לפי משפט 2 מתקיים <math>\underline S(f,P)\le\underline S(f,R)\le \overline S(f,R)\le\overline S(f,Q)</math>. {{משל}}
# תרומת קטע i ל-<math>\overline S(f,Q)</math>


לפי עצם ההגדרות <math>M_i\ge M_i'</math> ו-<math>M_i\ge M_i''</math>
===מסקנה 2===
לכן <math>\overline S(f,P)-\overline S(f,Q)\ge M_i\Delta x_i-(M_i(x_i'-x_{i-1})+M_i(x_i-x_i'))=M_i(\Delta x_i-((x_i'-x_{i-1})+(x_i-x_i')))=M_i(\Delta x_i-(x_i-x_{i-1}))=0</math>
עבור f כנ"ל מתקיים <math>\underline\int_a^b f\le\overline{\int}_a^b f</math>.
====הוכחה====
מסקנה 1 אומרת שלכל שתי חלוקות P,Q של <math>[a,b]</math> מתקיים <math>\underline S(f,P)\le\overline S(f,Q)</math> ולכן <math>\sup_P\underline S(f,P)\le\inf_Q\overline S(f,Q)</math>. כמו כן, לפי ההגדרה <math>\underline\int_a^b f=\sup_Q\underline S(f,Q)</math> ו-<math>\inf_P\overline S(f,P)=\overline{\int}_a^b f</math>. {{משל}}

גרסה אחרונה מ־14:17, 12 באוגוסט 2013

נושא ראשון:
אינטגרציה

הערה: האינטגרל הוא לא שטח שמתחת לגרף. למעשה, השטח מתחת לגרף מוגדר לפי האינטגרל.

דוגמת חישוב (ידני) של שטח שמתחת לגרף

הגרף של [math]\displaystyle{ y=x^2 }[/math] והמלבנים החוסמים (עם גבול ירוק) והחסומים (בצבע כחול).

נתון הגרף של [math]\displaystyle{ y=x^2 }[/math] ונרצה לחשב את השטח שמתחת לו בקטע [math]\displaystyle{ [0,1] }[/math]. נחלק את הקטע:

[math]\displaystyle{ 0=x_0\lt x_1\lt x_2\lt \dots\lt x_n=1 }[/math]

כך שבאופן כללי [math]\displaystyle{ x_k=k/n }[/math] (בגרף מוצג המקרה הפרטי [math]\displaystyle{ n=4 }[/math]).

מעל כל תת קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] נבנה "מלבן חוסם" שגובהו [math]\displaystyle{ \left({k\over n}\right)^2=x_k^2 }[/math]. שטח כל המלבנים הללו הוא "שטח חוסם"

[math]\displaystyle{ \overline S:=\sum_{k=1}^n\frac1n\left({k\over n}\right)^2=\frac1{n^3}\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6n^3} }[/math]

כמו כן, מעל כל תת קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] נבנה "מלבן חסום" שגובהו [math]\displaystyle{ \left({k-1\over n}\right)^2=x_{k-1}^2 }[/math]. ביחד מלבנים אלה מהווים "שטח חסום"

[math]\displaystyle{ \underline S:=\frac1n\sum_{k=1}^n\left({k-1\over n}\right)^2=\frac1{n^3}\sum_{k=1}^n(k-1)^2=\frac1{n^3}\sum_{k=1}^{n-1}k^2=\frac{(n-1)n(2n-1)}{6n^3} }[/math]

כעת, אם A מציין את השטח שמתחת לגרף, בוודאי ש-[math]\displaystyle{ \underline S\le A\le\overline S }[/math], ז"א [math]\displaystyle{ \frac{(n-1)(2n-1)}{6n^2}\le A\le\frac{(n+1)(2n+1)}{6n^2} }[/math]. הדבר נכון לכל [math]\displaystyle{ n\in\mathbb N }[/math] ולכן נוכל להשאיף את [math]\displaystyle{ n\to\infty }[/math] ולקבל [math]\displaystyle{ \frac13\le A\le\frac13 }[/math], לכן [math]\displaystyle{ A=\frac13 }[/math]. [math]\displaystyle{ \blacksquare }[/math]



הגדרה: תהי f מוגדרת בקטע I. נאמר שהפונקציה F קדומה ל-f ב-I אם [math]\displaystyle{ \forall x\in I:\ F'(x)=f(x) }[/math].

דוגמה: אם [math]\displaystyle{ f(x)=x^2 }[/math] אז [math]\displaystyle{ F(x)=\frac{x^3}3 }[/math].

משפט 0

אם F ו-G קדומות ל-f בקטע I אז קיים קבוע c כך ש-[math]\displaystyle{ F(x)=G(x)+c }[/math]

הוכחה

נגדיר [math]\displaystyle{ H(x)=F(x)-G(x) }[/math] ולכן [math]\displaystyle{ \forall x\in I:\ H'(x)=F'(x)-G'(x)=f(x)-f(x)=0 }[/math]. מכאן ש-H היא פונקציה קבועה ולכן יש קבוע c כך ש-[math]\displaystyle{ F(x)-G(x)=H(x)=c\implies F(x)=G(x)+c }[/math]. [math]\displaystyle{ \blacksquare }[/math]

הגדרה אינטואיטיבית: תהי [math]\displaystyle{ f(x)\ge0 }[/math] רציפה בקטע [math]\displaystyle{ [a,b] }[/math]. נסמן ב-[math]\displaystyle{ \int\limits_a^b f }[/math] את השטח שמתחת לגרף.

המשפט היסודי של חשבון אינטגרלי (בצורה אינטואיטיבית)

תהי [math]\displaystyle{ f(x)\ge0 }[/math] מוגדרת ורציפה ב-[math]\displaystyle{ [a,b] }[/math].

  1. לכל [math]\displaystyle{ x\in[a,b] }[/math] נגדיר [math]\displaystyle{ A(x)=\int\limits_a^x f }[/math] אזי [math]\displaystyle{ \forall x\in[a,b]:\ f(x)=A'(x) }[/math].
  2. אם F קדומה ל-f ב-[math]\displaystyle{ [a,b] }[/math] אז [math]\displaystyle{ \int\limits_a^b f=F(b)-F(a) }[/math].

הוכחה

הוכחה אינטואיטיבית למשפט היסודי של החשבון האינפיניטסימלי.png
  1. יהי x נתון. לפי ההגדרה [math]\displaystyle{ A'(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x} }[/math]. בגרף: [math]\displaystyle{ =A(x+\Delta x)-A(x) }[/math] השטח של החלק הירוק ו-[math]\displaystyle{ =\Delta x }[/math] בסיס החלק הירוק. לפיכך [math]\displaystyle{ =\frac{A(x+\Delta x)-A(x)}{\Delta x} }[/math] הגובה הממוצע של הפונקציה בחלק הירוק. לכן [math]\displaystyle{ =A'(x) }[/math] הגובה הממוצע של החלק הירוק (כאשר [math]\displaystyle{ \Delta x\to0 }[/math]) [math]\displaystyle{ f(x)= }[/math]. [math]\displaystyle{ \blacksquare }[/math]
  2. נתונה פונקציה קדומה F. מחלק 1 ידוע גם ש-A פונקציה קדומה (של f). לפי משפט 0 יש קבוע c כך ש-[math]\displaystyle{ F(x)=A(x)+c }[/math] ולכן [math]\displaystyle{ F(b)-F(a)=A(b)+c-(\underbrace{A(a)}_{=0}+c)=A(b)=\int\limits_a^b f }[/math]. [math]\displaystyle{ \blacksquare }[/math]

האינטגרל לפי דרבו

הקדמה - הגדרות

הגדרת הערכים באינטגרל לפי דרבו.png

תהי f מוגדרת וחסומה ע"י [math]\displaystyle{ m:=\inf f }[/math] ו- [math]\displaystyle{ M:=\sup f }[/math] בקטע [math]\displaystyle{ [a,b] }[/math]. נגדיר את התנודה של f ע"י [math]\displaystyle{ \Omega:=M-m }[/math]. כעת נגדיר חלוקה P של [math]\displaystyle{ [a,b] }[/math] כקבוצה [math]\displaystyle{ \{x_0,x_1,\dots,x_n\} }[/math] המקיימת: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math]. עוד נגדיר לכל k את אורך תת קטע מספר k להיות [math]\displaystyle{ \Delta x_k:=x_k-x_{k-1} }[/math] ואת הפרמטר של P להיות [math]\displaystyle{ \lambda(P):=\max_{k=1}^n\Delta x_k }[/math].

לכל k כך ש-[math]\displaystyle{ 1\le k\le n }[/math] נגדיר גם [math]\displaystyle{ M_k:=\sup\{f(x):\ x_{k-1}\le x\le x_k\} }[/math] וכן [math]\displaystyle{ m_k:=\inf\{f(x):\ x_{k-1}\le x\le x_k\} }[/math]. בהתאם לכך נגדיר:

  • שטח חוסם - הסכום העליון: [math]\displaystyle{ \overline S(f,P):=\sum_{k=1}^n M_k\Delta x_k }[/math]
  • שטח חסום - הסכום התחתון: [math]\displaystyle{ \underline S(f,P):=\sum_{k=1}^n m_k\Delta x_k }[/math]

משפט 1

בסימונים הנ"ל, עבור כל חלוקה P מתקיים [math]\displaystyle{ m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a) }[/math].

הוכחה

[math]\displaystyle{ =\sum_{k=1}^n\Delta x_k }[/math] סכום כל הרווחים בין n נקודות החלוקה [math]\displaystyle{ b-a= }[/math], לכן: [math]\displaystyle{ }[/math] [math]\displaystyle{ \sum_{k=1}^n m\Delta x_k }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ m(b-a) }[/math] [math]\displaystyle{ }[/math]
לכל k מתקיים [math]\displaystyle{ m\le m_k }[/math]. [math]\displaystyle{ }[/math] [math]\displaystyle{ \sum_{k=1}^n m_k\Delta x_k=\underline S(f,P) }[/math] [math]\displaystyle{ \le }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math] [math]\displaystyle{ \sum_{k=1}^n M_k \Delta x_k=\overline S(f,P) }[/math] [math]\displaystyle{ \le }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math] [math]\displaystyle{ \sum_{k=1}^n M\Delta x_k }[/math] [math]\displaystyle{ \le }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math] [math]\displaystyle{ M(b-a) }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ }[/math] [math]\displaystyle{ }[/math]

[math]\displaystyle{ \blacksquare }[/math]

נשים לב כי לפי משפט 1 המספרים [math]\displaystyle{ \overline S(f,P),\underline S(f,P) }[/math] חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).

לכן מוגדרים היטב ה"אינטגרל העליון" [math]\displaystyle{ \overline{\int}_a^b f:=\inf_P \overline S(f,P) }[/math] ו"האינטגרל התחתון" [math]\displaystyle{ \underline\int_a^b f:=\sup_P \underline S(f,P) }[/math].

הגדרת האינטגרל לפי דרבו

תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math]. נאמר ש-f אינטגרבילית לפי דרבו ב-[math]\displaystyle{ [a,b] }[/math] אם [math]\displaystyle{ \underline\int_a^b f=\overline{\int}_a^b f }[/math] ואם הם שווים אז נגדיר [math]\displaystyle{ \int\limits_a^b f }[/math] להיות הערך המשותף של [math]\displaystyle{ \underline\int f }[/math] ו-[math]\displaystyle{ \overline{\int} f }[/math].

דוגמה

בקטע [math]\displaystyle{ [a,b] }[/math] כלשהו נגדיר את פונקצית דיריכלה [math]\displaystyle{ D(x)=\begin{cases}1&x\in\mathbb Q\\0&x\not\in\mathbb Q\end{cases} }[/math]. נקח חלוקה כלשהי ל-[math]\displaystyle{ [a,b] }[/math]: [math]\displaystyle{ a=x_0\lt x_1\lt \dots\lt x_n=b }[/math].

לכל k מתקיים [math]\displaystyle{ M_k=\sup\{f(x):\ x_{k-1}\le x\le x_k\}=1 }[/math] וכן [math]\displaystyle{ m_k=\inf\{f(x):\ x_{k-1}\le x\le x_k\}=0 }[/math]. לכן [math]\displaystyle{ \overline S(f,P)=\sum_{k=1}^n M_k\Delta x_k=\sum_{k=1}^n 1\Delta x_k=b-a }[/math] ואילו [math]\displaystyle{ \underline S(f,P)=\sum_{k=1}^n m_k\Delta x_k=\sum_{k=1}^n 0\Delta x_k=0 }[/math]. מכאן [math]\displaystyle{ \underline\int_a^b f=\sup_P \underline S(f,P)=0 }[/math] ו-[math]\displaystyle{ \overline{\int}_a^b f=\inf_P \overline S(f,P)=b-a }[/math], וכייוון שאינם שווים f אינה אינטגרבילית. [math]\displaystyle{ \blacksquare }[/math]



הגדרה: תהי P חלוקה של קטע [math]\displaystyle{ [a,b] }[/math]. חלוקה Q של [math]\displaystyle{ [a,b] }[/math] נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.

משפט 2

תהי f מוגדרת וחסומה ב-[math]\displaystyle{ [a,b] }[/math], תהי P חלוקה של [math]\displaystyle{ [a,b] }[/math] ו-Q עידון של P ע"י הוספת r נקודות. אזי

[math]\displaystyle{ 0\le\overline S(f,P)-\overline S(f,Q)\le r\lambda(P)\Omega }[/math]

[math]\displaystyle{ 0\le\underline S(f,Q)-\underline S(f,P)\le r\lambda(P)\Omega }[/math]

(נזכיר ש-[math]\displaystyle{ \lambda(P)=\max_{1\le k\le n}\Delta x_k }[/math] ו-[math]\displaystyle{ \Omega=\sup_{x\in[a,b]} f(x)-\inf_{x\in[a,b]} f(x) }[/math])

כלומר, הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-[math]\displaystyle{ r\lambda(P)\Omega }[/math].

הוכחה

מקרה ראשון: [math]\displaystyle{ r=1 }[/math]. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת [math]\displaystyle{ x_i' }[/math] כך ש-[math]\displaystyle{ x_{i-1}\lt x_i'\lt x_i }[/math] עבור i כלשהו. בהתאם לכך נגדיר [math]\displaystyle{ M_i^-:=\sup\{f(x):\ x_{i-1}\le x\le x_i'\} }[/math] ו-[math]\displaystyle{ M_i^+:=\sup\{f(x):\ x_i'\le x\le x_i\} }[/math]. כמו כן, לא שינינו כל תת קטע [math]\displaystyle{ [x_{k-1},x_k] }[/math] עבור [math]\displaystyle{ k\not=i }[/math] כלשהו. לכן [math]\displaystyle{ \overline S(f,P)-\overline S(f,Q)=M_i\Delta x_i-\Big(M_i^-(x_i'-x_{i-1})+M_i^+(x_i-x_i')\Big) }[/math]

לפי ההגדרות [math]\displaystyle{ M_i\ge M_i^+,M_i^- }[/math] ולפיכך

[math]\displaystyle{ \begin{align}\overline S(f,P)-\overline S(f,Q)&\ge M_i\Delta x_i-\Big(M_i(x_i'-x_{i-1})+M_i(x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i'-x_{i-1}+x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i-x_{i-1})\Big)\\&=0\end{align} }[/math]

את ההמשך עשינו בשיעור שאחריו:

כמו כן,

[math]\displaystyle{ \begin{align}\overline S(f,P)-\overline S(f,Q)&\le M_i(x_i-x_{i-1})-m_i(x_i-x_{i-1})\\&=(M_i-m_i)(x_i-x_{i-1})\\&\le\Omega(x_i-x_{i-1})\\&\le\underbrace{r}_{=1}\lambda(P)\Omega\end{align} }[/math]

מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר [math]\displaystyle{ \Omega\lambda(P) }[/math] בכל אחת מ-r המפעמים. לכן מיד נסיק [math]\displaystyle{ 0\le\overline S(f,P)-\overline S(f,Q)\le r\Omega\lambda(P) }[/math].

ההוכחה לסכום תחתון דומה. [math]\displaystyle{ \blacksquare }[/math]

מסקנה 1

נקח f כנ"ל ונניח ש-P ו-Q הן שתי חלוקות כלשהן של [math]\displaystyle{ [a,b] }[/math]. אזי [math]\displaystyle{ \underline S(f,P)\le\overline S(f,Q) }[/math].

הוכחה

נבנה עידון משותף, ז"א [math]\displaystyle{ R=P\cup Q }[/math]. לפי משפט 2 מתקיים [math]\displaystyle{ \underline S(f,P)\le\underline S(f,R)\le \overline S(f,R)\le\overline S(f,Q) }[/math]. [math]\displaystyle{ \blacksquare }[/math]

מסקנה 2

עבור f כנ"ל מתקיים [math]\displaystyle{ \underline\int_a^b f\le\overline{\int}_a^b f }[/math].

הוכחה

מסקנה 1 אומרת שלכל שתי חלוקות P,Q של [math]\displaystyle{ [a,b] }[/math] מתקיים [math]\displaystyle{ \underline S(f,P)\le\overline S(f,Q) }[/math] ולכן [math]\displaystyle{ \sup_P\underline S(f,P)\le\inf_Q\overline S(f,Q) }[/math]. כמו כן, לפי ההגדרה [math]\displaystyle{ \underline\int_a^b f=\sup_Q\underline S(f,Q) }[/math] ו-[math]\displaystyle{ \inf_P\overline S(f,P)=\overline{\int}_a^b f }[/math]. [math]\displaystyle{ \blacksquare }[/math]

אוחזר מתוך "https://math-wiki.com/index.php?title=משתמש:אור_שחף/133_-_הרצאה/20.2.11&oldid=36698"