אטום: הבדלים בין גרסאות בדף
אין תקציר עריכה |
אין תקציר עריכה |
||
| שורה 28: | שורה 28: | ||
הצבת ערכה של <math>v</math> ממשוואת התנאי למסלולים סטציונריים נותנת ערך בדיד לרדיוסים: | הצבת ערכה של <math>v</math> ממשוואת התנאי למסלולים סטציונריים נותנת ערך בדיד לרדיוסים: | ||
<math>r_n=({{\epsilon_0 h^2} \over {\pi me^2}})n^2</math> | |||
האנרגיה של האלקטרון בכל אחד מהמצבים הסטציונריים מורכבת מהאנרגיה הקינטית ומהאנרגיה הפוטנציאלית של האלקטרון והגרעין כלומר: | |||
<math>E_T=E_p+E_k=-{e^2 \over {4 \pi \epsilon_0 r}}+{{mv^2} \over 2}</math> | |||
נקבל לאחר הצבת הרדיוס ואלגברה פשוטה כי מסלולי האנרגיה מקוונטטים ושווים: | |||
<math>E_n=-{{e^4m} \over {8 \pi \epsilon_0 r}}=-{{hcR} \over n^2}</math> | |||
כאשר <math>R={{e^4m} \over {8 \epsilon_0 ^2 h^3c}}</math>קבוע רידברג (Rydberg) | |||
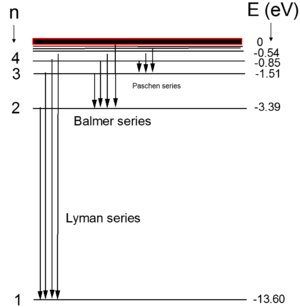
מתוך ביטוי זה ניתן לשרטט את רמות האנרגיה של אטום המימן (ראו איור 1). | |||
[[קובץ:ספקטרום פליטה אטום מימן.png|300px|מרכז|ממוזער|איור 1 - ספקטרום פליטה של אטום מימן]] | |||
הקווים הספקטרליים של אטומי המימן יוצרים מספר סדרות המתאימות למעברים של האטום מרמת אנרגיה גבוהה (n) לנמוכות יותר (m). סדרות אלו קיבלו שמות של המדענים: Lyman, Balmer, , Paschen, Brackett, Pfund. | |||
בעבודה זו נשתמש בסדרת Balmer כי בסדרה זו קוי הספקטרום המתקבלים הם בתחום הנראה. מודל בוהר נותן במדוייק את הקווים הספקטרליים של אטום המימן או דמוי מימן – שבקליפתו החיצונית אלקטרון אחד בלבד, אבל נכשל במקרים אחרים. לתיאור אטומים בעלי מספר אלקטרונים, יש להשתמש בתיאור הקוונטי המלא של האטום – לפי משוואת שרדינגר. | |||
בעבודה זו | |||
גרסה מ־15:54, 21 באוקטובר 2014
בשנת 1913 הציג נילס בוהר את מודל האטום שלו, לפיו בתוך האטום אלקטרונים נעים במספר בדיד של מסלולים, שבהם התנע הזוויתי של האלקטרונים הוא ביחידות שלמות של קבוע פלאנק. המודל הזה הסביר באופן יפה את ספקטרום הפליטה של אטום המימן, וההסבר האינטואיטיבי שעומד מאחוריו הוא שהאלקטרון מתנהג כמו גל, והמסלולים בהם הוא יכול לנוע דומים למצבים עצמיים של גלים.
בניסוי זה תוכלו לקבוע את רמות האנרגיה של אטום המימן לפי קווי ספקטרום הפליטה שלו ולמצוא את קבוע רידברג (Rydberg). חלקו שני של הניסוי הוא ביצוע גירסא של ניסוי פרנק-הרץ למציאת פוטנציאל עירור ופוטנציאל יינון של אטומי גז אציל.
רקע תיאורטי
מודל האטום של בוהר
עקב נפילתו של המודל הפלנטרי של רתרפורד, בשנת 1913 הציע נילס בוהר (N.Bohr), פיזיקאי דני צעיר שעבד במעבדתו של רתרפורד מודל מתוקן. הנחות בוהר הן עבור אטום המימן שהוא האטום הפשוט ביותר – בו יש אלקטרון אחד המסתובב מסביב לגרעין המכיל פרוטון בודד.
- אלקטרון יכול לנוע מסביב לגרעין רק במסלולים מעגליים מסויימים. כאשר האלקטרון נע באחד מהמסלולים הללו, אין הוא פולט קרינה אלקטרומגנטית למרות תנועתו המואצת. הנחה זו מנוגדת לחוקי הפיזיקה הקלאסית ובוהר קיבל אותה כאקסיומה.
התנאי למסלולים המותרים (נקראים גם סטציונריים) הוא: [math]\displaystyle{ mvr=n {h \over 2 \pi} }[/math] כאשר: [math]\displaystyle{ m }[/math]- מסת האלקטרון, [math]\displaystyle{ h }[/math]-קבוע פלנק ו- [math]\displaystyle{ n }[/math] מספר טבעי המאפיין את אינדקס המסלול.
- אלקטרון יכול לעבור ממסלול סטציונרי מסויים – בעל אינדקס [math]\displaystyle{ n }[/math] (בו האנרגיה גבוהה) למסלול סטציונרי אחר - בעל אינדקס [math]\displaystyle{ m }[/math] (בו האנרגיה נמוכה) ולהיפך ע"י פליטה או בליעה (בהתאמה) של פוטון בעל אנרגיה מתאימה:
[math]\displaystyle{ hf=|E_n-E_m| }[/math]
בהתבססו על הנחות יסוד אלה, חישב בוהר את רדיוסי המסלולים המותרים של אטום המימן, את אנרגיות המצבים היציבים ואורכי הגל של קווי ספקטרום הפליטה או ספקטרום הבליעה המתאימים למעבר של האטום ממצב יציב אחד לאחר.
לפי החוק השני של ניוטון, לחלקיק בתנועה מעגלית יש תאוצה צנטריפטלית שכיוונה כלפי מרכז המעגל. לכן על החלקיק פועל כח צנטריפטלי שכיוונו למרכז וגדלו [math]\displaystyle{ F={mv^2 \over r} }[/math] , הכח המאלץ את האלקטרון לנוע במעגל סביב הגרעין הוא הכח החשמלי המושך אותו אל הגרעין. מהשוואת שני כוחות אלו נקבל את רדיוס המסלול:
[math]\displaystyle{ r={e^2 \over {4 \pi \epsilon_0 m v^2}} }[/math]
כאשר [math]\displaystyle{ \epsilon_0=8.85*10^{-12} Fm^{-1} }[/math] הוא הקבוע הדיאלקטרי של החלל החופשי.
הצבת ערכה של [math]\displaystyle{ v }[/math] ממשוואת התנאי למסלולים סטציונריים נותנת ערך בדיד לרדיוסים:
[math]\displaystyle{ r_n=({{\epsilon_0 h^2} \over {\pi me^2}})n^2 }[/math]
האנרגיה של האלקטרון בכל אחד מהמצבים הסטציונריים מורכבת מהאנרגיה הקינטית ומהאנרגיה הפוטנציאלית של האלקטרון והגרעין כלומר:
[math]\displaystyle{ E_T=E_p+E_k=-{e^2 \over {4 \pi \epsilon_0 r}}+{{mv^2} \over 2} }[/math]
נקבל לאחר הצבת הרדיוס ואלגברה פשוטה כי מסלולי האנרגיה מקוונטטים ושווים:
[math]\displaystyle{ E_n=-{{e^4m} \over {8 \pi \epsilon_0 r}}=-{{hcR} \over n^2} }[/math]
כאשר [math]\displaystyle{ R={{e^4m} \over {8 \epsilon_0 ^2 h^3c}} }[/math]קבוע רידברג (Rydberg)
מתוך ביטוי זה ניתן לשרטט את רמות האנרגיה של אטום המימן (ראו איור 1).
הקווים הספקטרליים של אטומי המימן יוצרים מספר סדרות המתאימות למעברים של האטום מרמת אנרגיה גבוהה (n) לנמוכות יותר (m). סדרות אלו קיבלו שמות של המדענים: Lyman, Balmer, , Paschen, Brackett, Pfund.
בעבודה זו נשתמש בסדרת Balmer כי בסדרה זו קוי הספקטרום המתקבלים הם בתחום הנראה. מודל בוהר נותן במדוייק את הקווים הספקטרליים של אטום המימן או דמוי מימן – שבקליפתו החיצונית אלקטרון אחד בלבד, אבל נכשל במקרים אחרים. לתיאור אטומים בעלי מספר אלקטרונים, יש להשתמש בתיאור הקוונטי המלא של האטום – לפי משוואת שרדינגר.