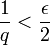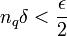הבדלים בין גרסאות בדף "אינטגרל מסויים"
(←פונקצית רימן) |
יהודה שמחה (שיחה | תרומות) (←פונקצית דיריכלה) |
||
| (4 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
[[קטגוריה:אינפי]] | [[קטגוריה:אינפי]] | ||
==הגדרה== | ==הגדרה== | ||
| − | תהי f פונקציה ממשית המוגדרת וחסומה בקטע <math>(a,b)</math>. אזי ישנן שתי הגדרות שקולות לאינטגרל | + | תהי <math>f</math> פונקציה ממשית המוגדרת וחסומה בקטע <math>(a,b)</math> . אזי ישנן שתי הגדרות שקולות לאינטגרל המסוים של <math>f</math> בקטע: |
| − | *הגדרה לפי ''' | + | *הגדרה לפי '''דארבו''': אם גבול [[סכום דרבו|סכומי דארבו]] התחתונים קיים ושווה לגבול סכומי דארבו העליונים אזי הפונקציה <math>f</math> '''אינטגרבילית''' בקטע והאינטגרל המסוים בקטע שווה לגבול סכומי דארבו. |
| − | *הגדרה לפי ''' | + | *הגדרה לפי '''רימאן''': אם גבול [[סכום רימן|סכומי רימאן]] קיים אזי <math>f</math> '''אינטגרבילית''' בקטע והאינטגרל המסוים בקטע שווה לגבול סכומי רימאן. |
==דוגמאות== | ==דוגמאות== | ||
| − | |||
===פונקצית דיריכלה=== | ===פונקצית דיריכלה=== | ||
| − | הוכח כי הפונקציה הבאה אינה אינטגרבילית בקטע <math>[0,1]</math>: | + | הוכח כי הפונקציה הבאה אינה אינטגרבילית בקטע <math>[0,1]</math> : |
| − | + | :<math>D(x)=\begin{cases}1&x\in\Q\\0&x\notin\Q\end{cases}</math> | |
| − | + | ;הוכחה. | |
| − | + | כיון שבכל [[חלוקה]] ובכל קטע קיימות גם נקודה רציונאלית וגם נקודה אי-רציונאלית, מתקיים לכל קטע: | |
| − | + | :<math>m_k=\inf\Big\{D(x)|x_{k-1}\le x\le x_k\Big\}=0</math> | |
| − | + | :<math>M_k=\sup\Big\{D(x)|x_{k-1}\le x\le x_k\Big\}=1</math> | |
| + | ולכן '''כל''' [[סכום דרבו|סכום דארבו]] תחתון שווה | ||
| + | :<math>\sum_k0\cdot\Delta_k=0</math> | ||
| − | + | וכמו כן '''כל''' [[סכום דרבו|סכום דארבו]] עליון שווה | |
| − | + | :<math>\sum_k1\cdot\Delta_k=\sum_k\Delta_k=\Big|[0,1]\Big|=1-0=1</math> | |
| − | + | שכן סכום אורכי כל תתי-הקטעים של החלוקה, שווה לאורך הקטע כולו. | |
| − | + | ||
| − | + | אם כך, גבול סכומי דארבו התחתונים הנו <math>0</math> והוא שונה מגבול סכומי דארבו העליונים שהוא <math>1</math>, ולכן הפונקציה '''אינה אינטגרבילית''' בקטע. | |
| − | + | ===פונקצית רימאן=== | |
| + | הוכח כי הפונקציה הבאה אינטגרבילית בקטע <math>[0,1]</math> , וכי מתקיים <math>\displaystyle\int\limits_0^1 R(x)dx=0</math> | ||
| − | == | + | :<math>R(x)=\begin{cases} \frac1{q}&x=\frac{p}{q}\\0&x\notin\Q\end{cases}</math> |
| − | + | כאשר <math>\frac{p}{q}</math> הוא '''השבר המצומצם''' של <math>x</math>. | |
| − | + | ;הוכחה. | |
| + | באופן דומה לתרגיל על פונקציית דיריכלה, קל לראות כי גבול סכומי דארבו התחתונים הוא <math>0</math>. לכן ניתן להוכיח כי גבול סכומי דרבו העליונים גם הוא <math>0</math>. | ||
| − | + | יהי <math>\epsilon>0</math> . צריך למצוא <math>\delta>0</math> כך ש'''לכל''' [[חלוקה]] עם [[חלוקה|פרמטר חלוקה]] קטן מ- <math>\delta</math> , מתקיים שמרחק סכום הדארבו העליון שלה מ- <math>0</math> קטן מ- <math>\epsilon</math> . | |
| − | + | כיון שמדובר בפונקציה חיובית, והגבול הנו <math>0</math> , צריך להוכיח שלכל חלוקה סכום הדארבו העליון קטן מ- <math>\epsilon</math> . | |
| − | + | ||
| − | + | כעת נראה כי לכל מספר טבעי <math>q</math> מספר הנקודות בקטע בהן <math>R(x)\ge\frac1{q}</math> הוא סופי, ונסמן מספר זה ב- <math>n_q</math> . | |
| − | + | אכן, הנקודות היחידות המקיימות תנאי זה הן <math>1,\frac12,\frac13,\frac23,\frac14,\frac24,\frac34,\ldots,\frac1{q},\ldots,\frac{q-1}{q}</math> (שימו לב שיתכן שחלק מהשברים הללו אינם מצומצמים ולכן יש אפילו פחות נקודות מאשר ברשימה הזו). | |
| + | כעת, בהנתן חלוקה <math>P</math> כלשהי, לכל היותר <math>n_q</math> קטעים מכילים נקודות בהן <math>R\ge\frac1{q}</math> , ולכן שטח הפונקציה במלבנים המתאימים לחלקים אלה הוא לכל היותר <math>1</math> כפול אורך הקטע. | ||
| − | + | בשאר הקטעים, גובה הפונקציה חסום על-ידי <math>\frac1{q}</math> . | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | בשאר הקטעים, גובה הפונקציה חסום על ידי <math>\ | + | |
לכן סכום הדרבו העליון הוא לכל היותר סכום הקטעים משני הסוגים האלו, ויתרה על כך: | לכן סכום הדרבו העליון הוא לכל היותר סכום הקטעים משני הסוגים האלו, ויתרה על כך: | ||
| − | + | :<math>\overline{S}(R,P)\le\frac1{q}\cdot\Big|[0,1]\Big|+n_q\cdot\lambda(P)</math> | |
כאשר <math>\lambda(P)</math> הוא אורך הקטע הכי ארוך בחלוקה. בוודאי אורכי הקטעים המכילים את הנקודות הגבוהות קטנים או שווים לו. | כאשר <math>\lambda(P)</math> הוא אורך הקטע הכי ארוך בחלוקה. בוודאי אורכי הקטעים המכילים את הנקודות הגבוהות קטנים או שווים לו. | ||
| שורה 65: | שורה 59: | ||
בסה"כ, נבחר q כך ש: | בסה"כ, נבחר q כך ש: | ||
| − | + | :<math>\frac1{q}<\frac{\epsilon}{2}</math> | |
| + | |||
| + | ולאחר מכן נבחר <math>\delta</math> כך ש: | ||
| + | :<math>n_q\delta<\frac{\epsilon}{2}</math> | ||
| − | + | וכך קיבלנו את שרצינו. <math>\blacksquare</math> | |
| − | + | ||
| − | + | ==חישוב האינטגרל המסוים== | |
| + | קיימות מספר שיטות לחישוב האינטגרל המסוים, כשהנפוצה והשימושית ביותר היא שימוש ב[[המשפט היסודי של החדוא|נוסחת ניוטון-לייבניץ]]. | ||
גרסה אחרונה מ־15:21, 12 בפברואר 2017
הגדרה
תהי  פונקציה ממשית המוגדרת וחסומה בקטע
פונקציה ממשית המוגדרת וחסומה בקטע 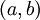 . אזי ישנן שתי הגדרות שקולות לאינטגרל המסוים של
. אזי ישנן שתי הגדרות שקולות לאינטגרל המסוים של  בקטע:
בקטע:
- הגדרה לפי דארבו: אם גבול סכומי דארבו התחתונים קיים ושווה לגבול סכומי דארבו העליונים אזי הפונקציה
 אינטגרבילית בקטע והאינטגרל המסוים בקטע שווה לגבול סכומי דארבו.
אינטגרבילית בקטע והאינטגרל המסוים בקטע שווה לגבול סכומי דארבו. - הגדרה לפי רימאן: אם גבול סכומי רימאן קיים אזי
 אינטגרבילית בקטע והאינטגרל המסוים בקטע שווה לגבול סכומי רימאן.
אינטגרבילית בקטע והאינטגרל המסוים בקטע שווה לגבול סכומי רימאן.
דוגמאות
פונקצית דיריכלה
הוכח כי הפונקציה הבאה אינה אינטגרבילית בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
- הוכחה.
כיון שבכל חלוקה ובכל קטע קיימות גם נקודה רציונאלית וגם נקודה אי-רציונאלית, מתקיים לכל קטע:
ולכן כל סכום דארבו תחתון שווה
וכמו כן כל סכום דארבו עליון שווה
שכן סכום אורכי כל תתי-הקטעים של החלוקה, שווה לאורך הקטע כולו.
אם כך, גבול סכומי דארבו התחתונים הנו 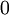 והוא שונה מגבול סכומי דארבו העליונים שהוא
והוא שונה מגבול סכומי דארבו העליונים שהוא 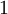 , ולכן הפונקציה אינה אינטגרבילית בקטע.
, ולכן הפונקציה אינה אינטגרבילית בקטע.
פונקצית רימאן
הוכח כי הפונקציה הבאה אינטגרבילית בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , וכי מתקיים
, וכי מתקיים 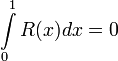
כאשר 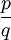 הוא השבר המצומצם של
הוא השבר המצומצם של  .
.
- הוכחה.
באופן דומה לתרגיל על פונקציית דיריכלה, קל לראות כי גבול סכומי דארבו התחתונים הוא 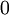 . לכן ניתן להוכיח כי גבול סכומי דרבו העליונים גם הוא
. לכן ניתן להוכיח כי גבול סכומי דרבו העליונים גם הוא 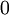 .
.
יהי 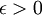 . צריך למצוא
. צריך למצוא 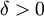 כך שלכל חלוקה עם פרמטר חלוקה קטן מ-
כך שלכל חלוקה עם פרמטר חלוקה קטן מ- 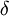 , מתקיים שמרחק סכום הדארבו העליון שלה מ-
, מתקיים שמרחק סכום הדארבו העליון שלה מ- 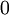 קטן מ-
קטן מ- 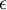 .
.
כיון שמדובר בפונקציה חיובית, והגבול הנו 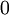 , צריך להוכיח שלכל חלוקה סכום הדארבו העליון קטן מ-
, צריך להוכיח שלכל חלוקה סכום הדארבו העליון קטן מ- 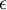 .
.
כעת נראה כי לכל מספר טבעי 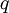 מספר הנקודות בקטע בהן
מספר הנקודות בקטע בהן 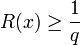 הוא סופי, ונסמן מספר זה ב-
הוא סופי, ונסמן מספר זה ב-  .
.
אכן, הנקודות היחידות המקיימות תנאי זה הן 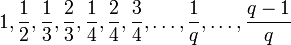 (שימו לב שיתכן שחלק מהשברים הללו אינם מצומצמים ולכן יש אפילו פחות נקודות מאשר ברשימה הזו).
(שימו לב שיתכן שחלק מהשברים הללו אינם מצומצמים ולכן יש אפילו פחות נקודות מאשר ברשימה הזו).
כעת, בהנתן חלוקה 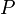 כלשהי, לכל היותר
כלשהי, לכל היותר  קטעים מכילים נקודות בהן
קטעים מכילים נקודות בהן 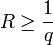 , ולכן שטח הפונקציה במלבנים המתאימים לחלקים אלה הוא לכל היותר
, ולכן שטח הפונקציה במלבנים המתאימים לחלקים אלה הוא לכל היותר 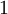 כפול אורך הקטע.
כפול אורך הקטע.
בשאר הקטעים, גובה הפונקציה חסום על-ידי  .
.
לכן סכום הדרבו העליון הוא לכל היותר סכום הקטעים משני הסוגים האלו, ויתרה על כך:
כאשר 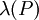 הוא אורך הקטע הכי ארוך בחלוקה. בוודאי אורכי הקטעים המכילים את הנקודות הגבוהות קטנים או שווים לו.
הוא אורך הקטע הכי ארוך בחלוקה. בוודאי אורכי הקטעים המכילים את הנקודות הגבוהות קטנים או שווים לו.
בסה"כ, נבחר q כך ש:
ולאחר מכן נבחר 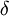 כך ש:
כך ש:
וכך קיבלנו את שרצינו. 
חישוב האינטגרל המסוים
קיימות מספר שיטות לחישוב האינטגרל המסוים, כשהנפוצה והשימושית ביותר היא שימוש בנוסחת ניוטון-לייבניץ.
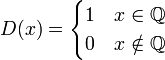
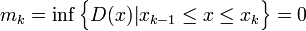
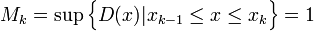
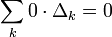
![\sum_k1\cdot\Delta_k=\sum_k\Delta_k=\Big|[0,1]\Big|=1-0=1](/images/math/5/1/a/51a134d80ded658964243613d9365c9d.png)
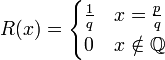
![\overline{S}(R,P)\le\frac1{q}\cdot\Big|[0,1]\Big|+n_q\cdot\lambda(P)](/images/math/c/6/8/c68db20920c389f4abb0ce495023243b.png)