אלגברה לינארית 1 תיכוניסטים קיץ תשעב/פתרון הבוחן
פתרון הבוחן:
שאלה 1:
נתון כי 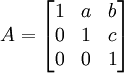 .
ו
.
ו 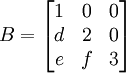 .
.
צריך למצוא מטריצות אלמנטריות 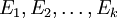 . כך ש
. כך ש 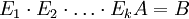 .
.
מדרגים את מטריצה  למטריצה
למטריצה  .
.
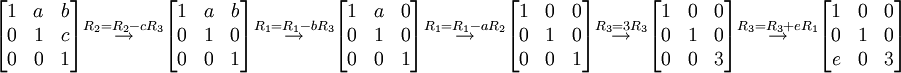
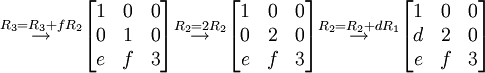
לכן מטריצות אלמנטריות מתאימות הן
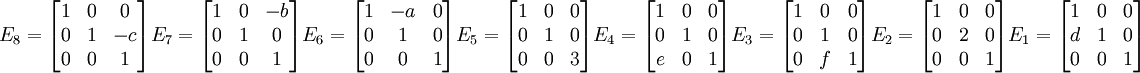
ומתקיים 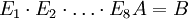 .
.
(זאת לא התשובה היחידה הנכונה, אבל זאת אחת הפשוטות)
שאלה 2:
נתונה מערכת המיוצגת על ידי המטריצה
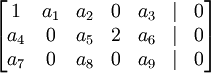
סעיף א) אם המטריצה מדורגת זה אומר ש 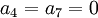 כי שניהם נמצאים מתחת לאיבר מוביל של השורה הראשונה.
כי שניהם נמצאים מתחת לאיבר מוביל של השורה הראשונה.
בנוסף אפשר לראות ש 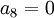 . הוכחה: נניח בשלילה ש
. הוכחה: נניח בשלילה ש 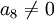 .
.
אם 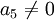 הוא נמצא מתחת לאיבר מוביל של השורה השניה.
הוא נמצא מתחת לאיבר מוביל של השורה השניה.
אם 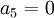 הוא יהיה איבר מוביל משמאל לאיבר המוביל של השורה השניה.
הוא יהיה איבר מוביל משמאל לאיבר המוביל של השורה השניה.
לכן 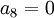 .
.
לגבי שאר הפרמטרים, כל בחירה שהיא שלהם תשאיר את המטריצה מדורגת ולכן לא ניתן לדעת מהם.
סעיף ב) אם  מדורגת קנונית אז
מדורגת קנונית אז 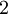 לא יכול להיות איבר מוביל של השורה השניה.
לא יכול להיות איבר מוביל של השורה השניה.
לכן, 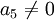 כלומר הוא איבר מוביל ולכן
כלומר הוא איבר מוביל ולכן 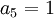 .
.
בנוסף 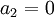 כי הוא מעל האיבר המוביל של השורה השניה.
כי הוא מעל האיבר המוביל של השורה השניה.
את הפרמטר 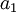 אי אפשר לקבוע.
גם את הפרמטרים
אי אפשר לקבוע.
גם את הפרמטרים 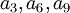 לא ניתן עדיין לקבוע בוודאות. כי יכול להיות ש
לא ניתן עדיין לקבוע בוודאות. כי יכול להיות ש 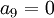 ואז
ואז 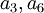 יכולים להיות כל מספר שהוא.
יכולים להיות כל מספר שהוא.
ויכול להיות ש 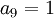 (ואז
(ואז 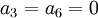 ).
).
סעיף ג) אם נתון שיש שני משתנים חופשיים, אז יש שלושה איברים מובילים ולכן
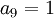 ולכן
ולכן 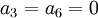 כי הם מעל איבר מוביל של השורה השלישית.
כי הם מעל איבר מוביל של השורה השלישית.
את 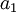 עדיין לא ניתן לקבוע.
עדיין לא ניתן לקבוע.
לכן קיבלנו
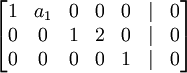
סעיף ד) פתרון פשוט של המערכת מוביל ל
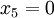

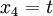

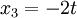

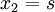

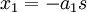
כלומר
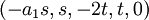 .
.
שאלה 3:
א) ![V = \mathbb{R}_3[x]](/images/math/3/a/a/3aad41f0bd657a950ed8c08671503724.png) ו
ו ![U = \{p\in \mathbb{R}_3[x] \mid p(0)=p(1)\}](/images/math/7/1/0/710c561c0c25456c06dfde2474c2bc3b.png)
נוכיח ש 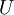 תת מרחב לפי הקריטריון המקוצר.
תת מרחב לפי הקריטריון המקוצר.
ראשית 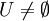 כי פולינום האפס נמצא בו.
כי פולינום האפס נמצא בו.
שנית, אם 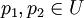 אז
אז
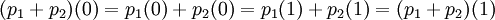
ואם 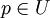 ו
ו 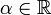 אז
אז
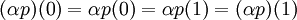 .
.
לכן 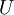 תת מרחב של
תת מרחב של  .
.
מציאת בסיס ומימד:
איבר כללי של  הוא מהצורה
הוא מהצורה 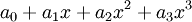
הדרישה 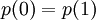 אומרת ש
אומרת ש
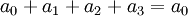
כלומר
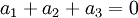
זאת מערכת של 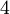 נעלמים עם משוואה אחת. נמצא את מרחב הפתרונות.
נעלמים עם משוואה אחת. נמצא את מרחב הפתרונות.
לפי פתרון המטריצה
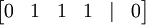
נקבל ש
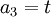
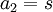
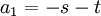
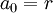
לכן איבר כללי בפתרון הוא
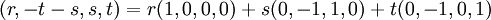
לכן בסיס יהיה הפולינומים שמיוצגים על ידי
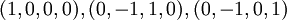
כלומר
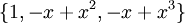
והמימד הוא 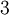 .
.
ב) 1) הפרכה. לוקחים ב 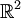 את
את
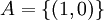
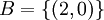
ואז
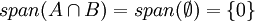
אבל 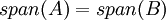
ולכן 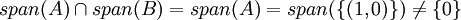
2) הוכחה:
נראה הכלה דו כיוונית
היות ולכל קבוצה 
מתקיים ש 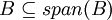
זה נכון גם כש 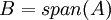
ולכן
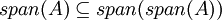 .
.
מצד שני אנחנו יודעים שאם  הוא מרחב וקטורי שמכיל את
הוא מרחב וקטורי שמכיל את  אז
אז 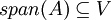 .
.
היות ו 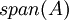 הוא מרחב וקטורי שמכיל את
הוא מרחב וקטורי שמכיל את 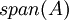 אז מתקיים
אז מתקיים 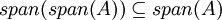 .
.
לכם בסך הכל
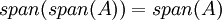 .
.