אלגברה לינארית 1 תיכוניסטים קיץ תשעב/פתרון מועד א'
תוכן עניינים
חלק א'
שאלה 1
ב. הפרכה:
נניח כי 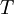 באמת חד חד ערכית.
באמת חד חד ערכית.
זה אומר כי 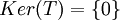 , ולכן
, ולכן 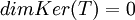 .
.
לפי משפט הדרגה 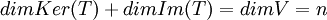
היות ו 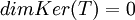 .
.
נקבל כי 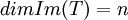 .
.
מצד שני, 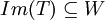 ולכן
ולכן 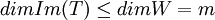 .
.
קיבלנו ש
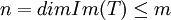
כלומר 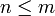 בסתירה לנתון ש
בסתירה לנתון ש 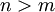 .
.
סתירה.
ולכן 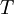 לא יכולה להיות חד חד ערכית.
לא יכולה להיות חד חד ערכית.
שאלה 2
ראשית נוכיח כי  בת"ל.
בת"ל.
נייצג את איברי  בתור וקטורי קוארדינטות ב
בתור וקטורי קוארדינטות ב 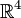 לפי הבסיס הסטנדרטי ונקבל
לפי הבסיס הסטנדרטי ונקבל
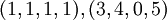 .
.
נשים וקטורים אלו בשורות מטריצה ונדרג אותה כדי לוודא שהם בלתי תלויים.
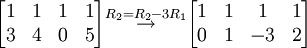
הגענו לצורה מדורגת בלי שקיבלנו שורת אפסים ולכן רשימת הוקטורים שהתחלנו איתה בת"ל.
(הערה: מי שהראה שכל צירוף 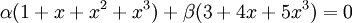 מחייב ש
מחייב ש 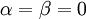 .
זאת גם תשובה טובה.
וגם מי שהראה שאין
.
זאת גם תשובה טובה.
וגם מי שהראה שאין 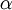 כך ש
כך ש 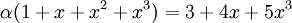 זו גם תשובה נכונה).
זו גם תשובה נכונה).
השלמת  לבסיס:
לבסיס:
הואיל ובמטריצה המדורגת שהגענו אליה יש איברים מובילים בעמודות 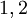 למדנו שאפשר להוסיף את
למדנו שאפשר להוסיף את 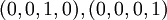 כלומר
כלומר  עבור כל עמודה
עבור כל עמודה 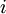 של משתנה חופשי.
של משתנה חופשי.
ולכן קיבלנו בסיס 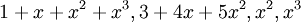 .
.
שימו לב שצריך לנמק למה מוסיפים את 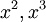 - מי שסתם כתב שמוסיפים אותם בלי הסבר איבד נקודות.
- מי שסתם כתב שמוסיפים אותם בלי הסבר איבד נקודות.
הסברים מקובלים:
יש איברים מובילים בעמודות 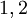 .
.
יש משתנים חופשיים בעמודות 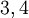
אם מוסיפים את 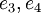 המטריצה נשארת מדורגת.
המטריצה נשארת מדורגת.
אם מוסיפים את 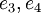 שורות המטריצה עדיין בלתי תלויות לינארית.
שורות המטריצה עדיין בלתי תלויות לינארית.
או משהו בסגנון.
יש סטודנטים שהמציאו שני וקטורים כלשהם (לאו דווקא 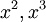 ) והראו שהקבוצה הנוצרת היא בת"ל/ פורשת ולכן לפי השלישי חינם היא בסיס.
יש סטודנטים שהמציאו שני וקטורים והוכיחו שהקבוצה הנוצרת בת"ל+ פורשת (שזה מיותר כי אפשר להשתמש בשלישי חינם)
גם התשובות האלה התקבלו, אמנם זה מייגע, אבל זה נכון.
) והראו שהקבוצה הנוצרת היא בת"ל/ פורשת ולכן לפי השלישי חינם היא בסיס.
יש סטודנטים שהמציאו שני וקטורים והוכיחו שהקבוצה הנוצרת בת"ל+ פורשת (שזה מיותר כי אפשר להשתמש בשלישי חינם)
גם התשובות האלה התקבלו, אמנם זה מייגע, אבל זה נכון.
יש סטודנטים שהשתמשו בעוד כל מיני דרכים מקוריות, חלק מהן היו נכונות.
שאלה 3
חלק ב'
נציג תשובות לפי הסדר כפי שהופיעו בגרסא הזאת של המבחן: מבחן מועד א'.
שאלה 1
קל להוכיח שלמערכת 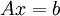 יש פתרון
יש פתרון 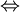
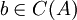 . ולכן א' וב' הם לא התשובה.
. ולכן א' וב' הם לא התשובה.
אם 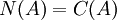 מתקיים גם
מתקיים גם 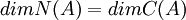 והיות ו
והיות ו 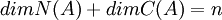 נקבל כי
נקבל כי  חייב להיות מספר זוגי ולכן
חייב להיות מספר זוגי ולכן 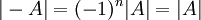 . לכן גם ד' היא טענה נכונה.
. לכן גם ד' היא טענה נכונה.
ג' שגוי. כי 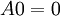 ו
ו 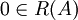 .
.
לכן התשובה היא ג'.