הבדלים בין גרסאות בדף "אלגברה לינארית 1 תיכוניסטים קיץ תשעג/פתרון הבוחן"
איתמר שטיין (שיחה | תרומות) (יצירת דף עם התוכן "===שאלה 1=== לפי כפל עמודה עמודה קל לראות שמחפשים 3 עמודות <math>C_1(A),C_2(A),C_3(A)</math> שמקיימות <math>\begi...") |
איתמר שטיין (שיחה | תרומות) (←שאלה 1) |
||
| שורה 24: | שורה 24: | ||
<math>7^3</math> פתרונות. | <math>7^3</math> פתרונות. | ||
| + | |||
| + | |||
| + | ===שאלה 2=== | ||
| + | |||
| + | <math>A</math> היא מטריצה הפיכה, ולכן הצורה המדורגת קנונית שלה היא <math>I</math>. | ||
| + | |||
| + | אם נסמן ב E_1,\ldtos,E_5 את המטריצות האלמנטריות המתאימות לפעולות הנתונות. אז בעצם | ||
| + | |||
| + | <math>E_5E_4E_3E_2E_1A=I</math> | ||
| + | |||
| + | ולכן <math>A=(E_1)^{-1}(E_2)^{-1}(E_3)^{-1}(E_4)^{-1}(E_5)^{-1}I</math> | ||
| + | |||
| + | כלומר, אם נבצע את הפעולות ההפוכות בסדר הפוך על <math>I</math>, נגיע ל <math>A</math>. | ||
| + | |||
| + | הפעולות ההפוכות בסדר הפוך הן: | ||
| + | |||
| + | <math>R_1 \leftrightarrow R_5</math> | ||
| + | |||
| + | <math>R_1 = R_1+2R_2</math> | ||
| + | |||
| + | <math>R_1 \leftrightarrow R_3</math> | ||
| + | |||
| + | <math>R_1 = R_1 -R_2</math> | ||
| + | |||
| + | <math>R_1 = \frac{1}{2} R_1</math> | ||
| + | |||
| + | ולכן קל לחשב ש | ||
| + | |||
| + | <math>A=\begin{bmatrix} | ||
| + | |||
| + | 0 & -\frac{1}{2} & \frac{1}{2} & 0 & 0 \\ | ||
| + | |||
| + | 0 & 1 & 0 & 0 & 0 \\ | ||
| + | |||
| + | 0 & 0 & 0 & 2 & 1 \\ | ||
| + | |||
| + | 0 & 0 & 0 & 1 & 0 \\ | ||
| + | |||
| + | 1 & 0 & 0 & 0 & 0 \\ | ||
| + | |||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | |||
| + | היות ו | ||
| + | |||
| + | <math>A=(E_1)^{-1}(E_2)^{-1}(E_3)^{-1}(E_4)^{-1}(E_5)^{-1}I</math> | ||
| + | |||
| + | נקבל ש | ||
| + | |||
| + | <math>A^-1=E_5E_4E_3E_2E_1I</math> | ||
| + | |||
| + | כלומר צריך לבצע את הפעולות האלה על <math>I</math> כדי להגיע ל <math>A^-1</math> | ||
| + | |||
| + | לכן קל לחשב ש | ||
| + | |||
| + | <math>A^-1=\begin{bmatrix} | ||
| + | |||
| + | 0 & 0 & 0 & 0 & 1 \\ | ||
| + | |||
| + | 0 & 1 & 0 & 0 & 0 \\ | ||
| + | |||
| + | 2 & 1 & 0 & 0 & 0 \\ | ||
| + | |||
| + | 0 & 0 & 0 & 1 & 0 \\ | ||
| + | |||
| + | 0 & 0 & 1 & -2 & 0 \\ | ||
| + | |||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | |||
| + | היות ו <math>A^-1=E_5E_4E_3E_2E_1I</math> נקבל ש | ||
| + | |||
| + | <math>(E_1)^{-1}(E_2)^{-1}(E_3)^{-1}(E_4)^{-1}(E_5)^{-1}A^-1=I</math> | ||
| + | |||
| + | כלומר הפעולות שצריך לעשות כדי לדרג את <math>A^-1</math> הן הפעולות שהפוכות לפעולת הכתובות בסדר הפוך כלומר: | ||
| + | |||
| + | <math>R_1 \leftrightarrow R_5</math> | ||
| + | |||
| + | <math>R_1 = R_1+2R_2</math> | ||
| + | |||
| + | <math>R_1 \leftrightarrow R_3</math> | ||
| + | |||
| + | <math>R_1 = R_1 -R_2</math> | ||
| + | |||
| + | <math>R_1 = \frac{1}{2} R_1</math> | ||
| + | |||
| + | (זאת כמובן לא הדרך היחידה להביא את <math>A^-1</math> לצורה מדורגת קנונית, אבל זאת הדרך הכי פשוטה.) | ||
גרסה מ־06:33, 16 באוגוסט 2013
שאלה 1
לפי כפל עמודה עמודה קל לראות שמחפשים 3 עמודות 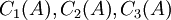
שמקיימות
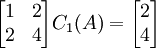
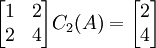
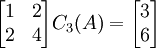
כך שקיבלנו 3 משוואות, כל אחת בשני נעלמים.
אם נפתור את המשוואה הראשונה
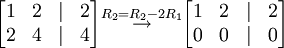
נראה שיש משתנה חופשי אחד (ואין שורות סתירה) ולכן יש 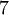 פתרונות.
פתרונות.
אותה הדבר קורה בשביל שאר המשוואות ולכן בסך הכל יש
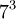 פתרונות.
פתרונות.
שאלה 2
 היא מטריצה הפיכה, ולכן הצורה המדורגת קנונית שלה היא
היא מטריצה הפיכה, ולכן הצורה המדורגת קנונית שלה היא 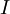 .
.
אם נסמן ב E_1,\ldtos,E_5 את המטריצות האלמנטריות המתאימות לפעולות הנתונות. אז בעצם
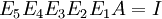
ולכן 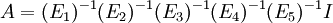
כלומר, אם נבצע את הפעולות ההפוכות בסדר הפוך על 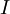 , נגיע ל
, נגיע ל  .
.
הפעולות ההפוכות בסדר הפוך הן:
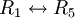
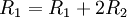
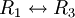
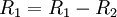
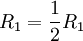
ולכן קל לחשב ש

היות ו
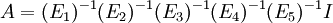
נקבל ש
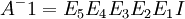
כלומר צריך לבצע את הפעולות האלה על 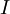 כדי להגיע ל
כדי להגיע ל 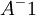
לכן קל לחשב ש
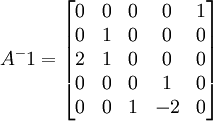
היות ו 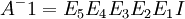 נקבל ש
נקבל ש
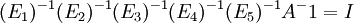
כלומר הפעולות שצריך לעשות כדי לדרג את 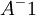 הן הפעולות שהפוכות לפעולת הכתובות בסדר הפוך כלומר:
הן הפעולות שהפוכות לפעולת הכתובות בסדר הפוך כלומר:
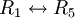
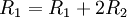
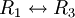
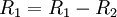
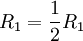
(זאת כמובן לא הדרך היחידה להביא את 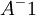 לצורה מדורגת קנונית, אבל זאת הדרך הכי פשוטה.)
לצורה מדורגת קנונית, אבל זאת הדרך הכי פשוטה.)