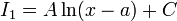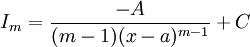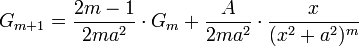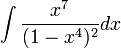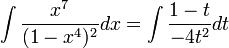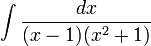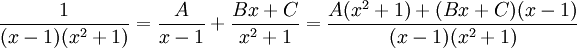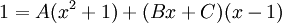הבדלים בין גרסאות בדף "אלגוריתם לביצוע אינטגרל על פונקציה רציונאלית"
מתוך Math-Wiki
יהודה שמחה (שיחה | תרומות) |
יהודה שמחה (שיחה | תרומות) |
||
| שורה 6: | שורה 6: | ||
==מצב ראשון <math>\deg(p)=\deg(q)-1</math>== | ==מצב ראשון <math>\deg(p)=\deg(q)-1</math>== | ||
| − | ניתן למצוא קבוע | + | ניתן למצוא קבוע <math>c</math> כך ש- <math>h=cp-q'</math> כך ש- <math>\deg(h)<\deg(q)-1</math> . |
אז רושמים <math>\int\frac{p}{q}=\int\frac{q'+h}{c\cdot q}=\frac{\ln(q)}{c}+\int\frac{h}{c\cdot q}</math> | אז רושמים <math>\int\frac{p}{q}=\int\frac{q'+h}{c\cdot q}=\frac{\ln(q)}{c}+\int\frac{h}{c\cdot q}</math> | ||
| שורה 13: | שורה 13: | ||
==מצב שני <math>\deg(p)<\deg(q)-1</math>== | ==מצב שני <math>\deg(p)<\deg(q)-1</math>== | ||
| − | *נפרק את | + | *נפרק את <math>q</math> לגורמים אי-פריקים: |
| + | |||
:<math>q(x)=(x-a_1)^{n_1}\cdots(x-a_k)^{n_k}\cdot(x^2+c_1x+b_1)^{m_1}\cdots(x^2+c_jx+b_j)^{m_j}</math> | :<math>q(x)=(x-a_1)^{n_1}\cdots(x-a_k)^{n_k}\cdot(x^2+c_1x+b_1)^{m_1}\cdots(x^2+c_jx+b_j)^{m_j}</math> | ||
*כעת, נפרק את הפונקציה הרציונאלית לשברים חלקיים: | *כעת, נפרק את הפונקציה הרציונאלית לשברים חלקיים: | ||
| + | |||
:<math>\frac{p}{q}=\Big[\frac{A_{1,1}}{x-a_1}+\frac{A_{1,2}}{(x-a_1)^2}+\cdots+\frac{A_{1,n_1}}{(x-a_1)^{n_1}}\Big]+\cdots+ | :<math>\frac{p}{q}=\Big[\frac{A_{1,1}}{x-a_1}+\frac{A_{1,2}}{(x-a_1)^2}+\cdots+\frac{A_{1,n_1}}{(x-a_1)^{n_1}}\Big]+\cdots+ | ||
\Big[\frac{A_{k,1}}{x-a_k}+\frac{A_{k,2}}{(x-a_k)^2}+\cdots+\frac{A_{k,n_k}}{(x-a_k)^{n_k}}\Big]+ | \Big[\frac{A_{k,1}}{x-a_k}+\frac{A_{k,2}}{(x-a_k)^2}+\cdots+\frac{A_{k,n_k}}{(x-a_k)^{n_k}}\Big]+ | ||
</math> | </math> | ||
| + | |||
:<math>+\Big[\frac{B_{1,1}x+C_{1,1}}{x^2+c_1x+b_1}+\frac{B_{1,2}x+C_{1,2}}{(x^2+c_1x+b_1)^2}+\cdots+\frac{B_{1,m_1}x+C_{1,m_1}}{(x^2+c_1x+b_1)^{m_1}}\Big]+\cdots</math> | :<math>+\Big[\frac{B_{1,1}x+C_{1,1}}{x^2+c_1x+b_1}+\frac{B_{1,2}x+C_{1,2}}{(x^2+c_1x+b_1)^2}+\cdots+\frac{B_{1,m_1}x+C_{1,m_1}}{(x^2+c_1x+b_1)^{m_1}}\Big]+\cdots</math> | ||
| שורה 26: | שורה 29: | ||
===אינטגרל מהצורה <math>I_m=\int\frac{A}{(x-a)^m}</math>=== | ===אינטגרל מהצורה <math>I_m=\int\frac{A}{(x-a)^m}</math>=== | ||
| − | נבצע הצבה <math>t=x-a</math> על מנת לקבל: | + | נבצע הצבה <math>t=x-a</math> על-מנת לקבל: |
| − | :<math>I_1= | + | |
| + | :<math>I_1=A\ln(x-a)+C</math> | ||
| + | |||
:<math>I_m=\frac{-A}{(m-1)(x-a)^{m-1}}+C</math> | :<math>I_m=\frac{-A}{(m-1)(x-a)^{m-1}}+C</math> | ||
===אינטגרל מהצורה <math>I_m=\int\frac{A}{(x^2+bx+c)^m}</math> (כאשר המכנה אי-פריק)=== | ===אינטגרל מהצורה <math>I_m=\int\frac{A}{(x^2+bx+c)^m}</math> (כאשר המכנה אי-פריק)=== | ||
| − | *נבצע השלמה לריבוע על-מנת לקבל את האינטגרל <math>I_m=\int\frac{A}{(\ | + | *נבצע השלמה לריבוע על-מנת לקבל את האינטגרל <math>I_m=\int\frac{A}{\left(\left[x+\frac{b}{2}\right]^2+\left[c-\left(\frac{b}{2}\right)^2\right]\right)^m}</math> |
*כעת, בעזרת הצבה לינארית פשוטה נעבור לאינטגרל מהצורה <math>G_m=\int\frac{A}{(x^2+a^2)^m}</math> | *כעת, בעזרת הצבה לינארית פשוטה נעבור לאינטגרל מהצורה <math>G_m=\int\frac{A}{(x^2+a^2)^m}</math> | ||
| שורה 47: | שורה 52: | ||
*לחלק הנותר נבצע הצבה <math>t=x^2+bx+c</math> לקבל אינטגרל פתיר מהצורה <math>I_m=\int\frac{A}{t^m}</math> | *לחלק הנותר נבצע הצבה <math>t=x^2+bx+c</math> לקבל אינטגרל פתיר מהצורה <math>I_m=\int\frac{A}{t^m}</math> | ||
| − | ==מצב שלישי <math>deg(p)=deg(q)</math>== | + | ==מצב שלישי <math>\deg(p)=\deg(q)</math>== |
| − | *קיים קבוע | + | *קיים קבוע <math>c</math> כך שקיים פולינום <math>h</math> המקיים <math>h=cp-q</math> וגם <math>\deg(h)<\deg(q)</math> . |
*נפריד את האינטגרל לשניים <math>\int\frac{p}{q}=\int\frac{q+h}{c\cdot q}=\int 1+\int\frac{h}{q}</math> | *נפריד את האינטגרל לשניים <math>\int\frac{p}{q}=\int\frac{q+h}{c\cdot q}=\int 1+\int\frac{h}{q}</math> | ||
| שורה 54: | שורה 59: | ||
*נחזור למצב הראשון או השני להמשך החישוב. | *נחזור למצב הראשון או השני להמשך החישוב. | ||
| − | ==מצב רביעי <math>deg(p)>deg(q)</math>== | + | ==מצב רביעי <math>\deg(p)>\deg(q)</math>== |
*נבצע חלוקת פולינומים על-מנת לקבל את הנוסחא <math>p(x)=a(x)q(x)+r(x)</math> כאשר מתקיים <math>\deg(r)<\deg(q)</math> | *נבצע חלוקת פולינומים על-מנת לקבל את הנוסחא <math>p(x)=a(x)q(x)+r(x)</math> כאשר מתקיים <math>\deg(r)<\deg(q)</math> | ||
| שורה 67: | שורה 72: | ||
===דוגמא 1=== | ===דוגמא 1=== | ||
:<math>\int\frac{x^7}{(1-x^4)^2}dx</math> | :<math>\int\frac{x^7}{(1-x^4)^2}dx</math> | ||
| + | |||
בדוגמא זו '''ניתן''' להפעיל את האלגוריתם אך עדיף לבצע את ההצבה <math>t=1-x^4</math> ולקבל | בדוגמא זו '''ניתן''' להפעיל את האלגוריתם אך עדיף לבצע את ההצבה <math>t=1-x^4</math> ולקבל | ||
| + | |||
:<math>\int\frac{x^7}{(1-x^4)^2}dx=\int\frac{1-t}{-4t^2}dt</math> | :<math>\int\frac{x^7}{(1-x^4)^2}dx=\int\frac{1-t}{-4t^2}dt</math> | ||
==דוגמא 2== | ==דוגמא 2== | ||
:<math>\int\frac{dx}{(x-1)(x^2+1)}</math> | :<math>\int\frac{dx}{(x-1)(x^2+1)}</math> | ||
| + | |||
נפרק לשברים חלקיים | נפרק לשברים חלקיים | ||
| + | |||
:<math>\frac{1}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}=\frac{A(x^2+1)+(Bx+C)(x-1)}{(x-1)(x^2+1)}</math> | :<math>\frac{1}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}=\frac{A(x^2+1)+(Bx+C)(x-1)}{(x-1)(x^2+1)}</math> | ||
| − | לכן | + | |
| + | לכן | ||
| + | |||
:<math>1=A(x^2+1)+(Bx+C)(x-1)</math> | :<math>1=A(x^2+1)+(Bx+C)(x-1)</math> | ||
גרסה מ־11:30, 3 בנובמבר 2016
תוכן עניינים
אלגוריתם מלא לביצוע אינטגרל על פונקציה רציונאלית
תהי פונקציה מהצורה 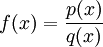 כאשר
כאשר 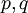 פולינומים. נתאר אלגוריתם לחישוב
פולינומים. נתאר אלגוריתם לחישוב 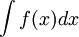 .
.
עובדה. כל פולינום אפשר לפרק מעל הממשיים לגורמים ממעלה 1 ו-2 (עובדה זו נובעת מכך ששדה המספרים הממשיים הוא שדה סגור ממשית. איננו מטפלים כאן בבעיה האלגוריתמית של פירוק פולינום לגורמים).
מצב ראשון 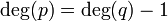
ניתן למצוא קבוע 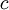 כך ש-
כך ש- 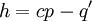 כך ש-
כך ש- 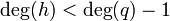 .
.
אז רושמים 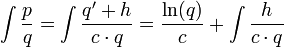
וממשיכים לשלב הבא:
מצב שני 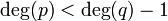
- נפרק את
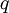 לגורמים אי-פריקים:
לגורמים אי-פריקים:
- כעת, נפרק את הפונקציה הרציונאלית לשברים חלקיים:
- נעשה מכנה משותף ונשווה בין הפולינום שנקבל במונה לפולינום
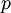 , מקדם מקדם. נקבל מערכת משוואות ממנה נחשב את הקבועים
, מקדם מקדם. נקבל מערכת משוואות ממנה נחשב את הקבועים 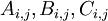 .
. - נחשב כל מחובר בנפרד:
אינטגרל מהצורה 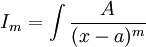
נבצע הצבה 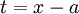 על-מנת לקבל:
על-מנת לקבל:
אינטגרל מהצורה 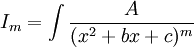 (כאשר המכנה אי-פריק)
(כאשר המכנה אי-פריק)
- נבצע השלמה לריבוע על-מנת לקבל את האינטגרל
![I_m=\int\frac{A}{\left(\left[x+\frac{b}{2}\right]^2+\left[c-\left(\frac{b}{2}\right)^2\right]\right)^m}](/images/math/6/d/3/6d3073076d2ef864f7e3d9d753881d35.png)
- כעת, בעזרת הצבה לינארית פשוטה נעבור לאינטגרל מהצורה
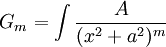
- נעזר בנוסחא הרקורסיבית הבאה:
אינטגרל מהצורה 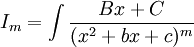 (כאשר המכנה אי-פריק)
(כאשר המכנה אי-פריק)
- דבר ראשון, בדומה למצב הראשון, נצמצם את הבעיה לאינטגרל מהצורה
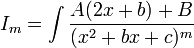
- את החלק
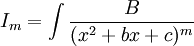 פותרים לפי הנוסחא לעיל
פותרים לפי הנוסחא לעיל
- לחלק הנותר נבצע הצבה
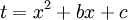 לקבל אינטגרל פתיר מהצורה
לקבל אינטגרל פתיר מהצורה 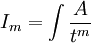
מצב שלישי 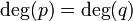
- קיים קבוע
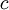 כך שקיים פולינום
כך שקיים פולינום 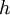 המקיים
המקיים 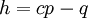 וגם
וגם 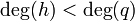 .
.
- נפריד את האינטגרל לשניים
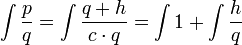
- נחזור למצב הראשון או השני להמשך החישוב.
מצב רביעי 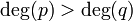
- נבצע חלוקת פולינומים על-מנת לקבל את הנוסחא
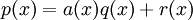 כאשר מתקיים
כאשר מתקיים 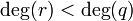
- מתקיים
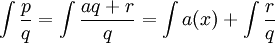
- נמשיך לפתור את האינטגרל בעזרת המצב הראשון או השני.
מצב חמישי 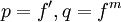
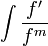 מבצעים את ההצבה
מבצעים את ההצבה 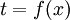
דוגמאות
דוגמא 1
בדוגמא זו ניתן להפעיל את האלגוריתם אך עדיף לבצע את ההצבה 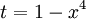 ולקבל
ולקבל
דוגמא 2
נפרק לשברים חלקיים
לכן
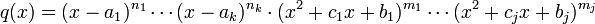
![\frac{p}{q}=\Big[\frac{A_{1,1}}{x-a_1}+\frac{A_{1,2}}{(x-a_1)^2}+\cdots+\frac{A_{1,n_1}}{(x-a_1)^{n_1}}\Big]+\cdots+
\Big[\frac{A_{k,1}}{x-a_k}+\frac{A_{k,2}}{(x-a_k)^2}+\cdots+\frac{A_{k,n_k}}{(x-a_k)^{n_k}}\Big]+](/images/math/6/4/b/64b42c6ce8ccbdd5e6c9fead2830cb1b.png)
![+\Big[\frac{B_{1,1}x+C_{1,1}}{x^2+c_1x+b_1}+\frac{B_{1,2}x+C_{1,2}}{(x^2+c_1x+b_1)^2}+\cdots+\frac{B_{1,m_1}x+C_{1,m_1}}{(x^2+c_1x+b_1)^{m_1}}\Big]+\cdots](/images/math/a/9/b/a9b72b34bc6e2cfa5e1a19f85a30ff82.png)