הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 1"

גרסה מ־09:50, 15 באוקטובר 2018

תוכן עניינים

1 הגדרה
- 1.1 חלק ממשי וחלק מדומה
2 נורמה וצמוד
- 2.1 נורמה
  - 2.1.1 תכונות הנורמה
    - 2.1.1.1 אש"מ ההפוך - בהרצאה
- 2.2 צמוד
3 מציאת הופכי וחילוק
- 3.1 תרגיל
  - 3.1.1 פתרון
- 3.2 תרגיל
4 תרגילים
- 4.1 תרגיל
  - 4.1.1 פתרון
- 4.2 תרגיל

הגדרה

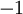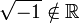כידוע אין שורש ממשי למספר $-1$ . כלומר $\sqrt{-1}\notin \mathbb{R}$ .

בתחילת הקורס נלמד על מבנה מתמטי בו יש שורש ל 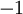$-1$ : שדה המספרים המרוכבים!

אז מי הם בעצם המספרים המרוכבים? בעצם מה שאנחנו צריכים להגדיר כאן זה שלושה דברים:

1. האיברים עצמם - המספרים המרוכבים.

2. איך לחבר ביניהם.

3. איך להכפיל ביניהם.

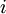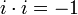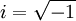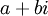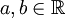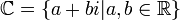נסמן ב $i$ איבר מסויים, ונגדיר $i\cdot i=-1$ . במילים אחרות $i=\sqrt{-1}$ . המספרים המרוכבים הם כל המספרים מהצורה $a+bi$ כאשר $a,b\in \mathbb{R}$ . כלומר, $\mathbb{C}=\{a+bi|a,b\in \mathbb{R}\}$ . שימו לב שכמובן שהמספרים הממשיים מוכלים במרוכבים, פשוט לוקחים $b=0$ .

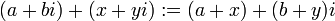חיבור: $(a+bi)+(x+yi):=(a+x)+(b+y)i$ .

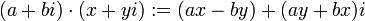כפל: $(a+bi)\cdot (x+yi):=(ax-by)+(ay+bx)i$ .

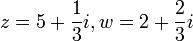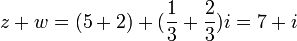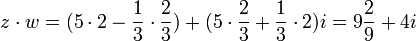לדוגמא: נסמן $z=5+\frac{1}{3}i,w=2+\frac{2}{3}i$ . נקבל: $z+w=(5+2)+(\frac{1}{3}+\frac{2}{3})i=7+i$ , וכן $z\cdot w=(5\cdot 2-\frac{1}{3}\cdot \frac{2}{3})+(5\cdot \frac{2}{3}+\frac{1}{3}\cdot 2)i=9\frac{2}{9}+4i$ .

חלק ממשי וחלק מדומה

יהי 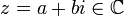$z=a+bi\in \mathbb{C}$ . נגדיר את החלק הממשי שלו להיות: 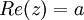$Re(z)=a$ , ואת החלק המדומה שלו להיות 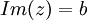$Im(z)=b$ . שימו לב שגם החלק הממשי וגם החלק המדומה הם מספרים ממשיים!!!

דוגמא: 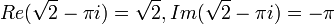$Re(\sqrt{2}-\pi i)=\sqrt{2},Im(\sqrt{2}-\pi i)=-\pi$ .

שימו לב שמספר מרוכב 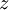$z$ הוא ממשי אם ורק אם $Im(z)=0$ .

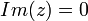מספר מרוכב 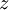$z$ נקרא מדומה טהור אם 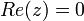$Re(z)=0$ . למשל $2i$ .

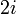נורמה וצמוד

נורמה

במספרים הממשיים יש לנו ערך מוחלט, והוא מוגדר כמרחק של המספר מאפס. נגדיר משהו דומה על המספרים המרוכבים - הנורמה (ויש שקוראים לזה ערך מוחלט). הנורמה זו בעצם פונקציה 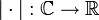$|\cdot |:\mathbb{C}\to \mathbb{R}$ המוגדרת ע"י: 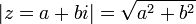$|z=a+bi|=\sqrt{a^2+b^2}$ . מאיפה הגיעה הפונקציה הזו? אם נתבונן על המספרים המרוכבים במערכת צירים נוכל לשים לב שהנורמה היא המרחק (האוקלידי) מראשית הצירים. דוגמאות נחמדות כיד המתרגל הטובה עליו.

תכונות הנורמה

1. כפליות: 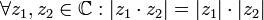$\forall z_1,z_2\in \mathbb{C}:|z_1\cdot z_2|=|z_1|\cdot |z_2|$ .

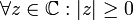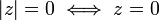2. אי שליליות: $\forall z\in \mathbb{C}:|z|\geq 0$ , ומתקיים: $|z|=0\iff z=0$ .

3. אי שיוויון המשולש: 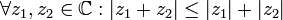$\forall z_1,z_2\in \mathbb{C}:|z_1+z_2|\leq |z_1|+|z_2|$ .

אש"מ ההפוך - בהרצאה

הוכיחו: 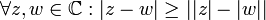$\forall z,w\in \mathbb{C}:|z-w|\geq ||z|-|w||$ .

הערה: זה נקרא אש"מ ההפוך.

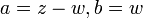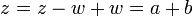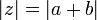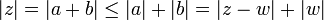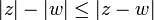פתרון: נסמן $a=z-w,b=w$ . נשים לב ש $z=z-w+w=a+b$ ולכן $|z|=|a+b|$ . כעת מאי שיוויון המשולש נקבל: $|z|=|a+b|\leq |a|+|b|=|z-w|+|w|$ . נעביר אגפים לקבל $|z|-|w|\leq |z-w|$ .

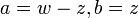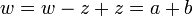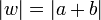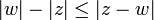בדומה, נסמן $a=w-z,b=z$ . נשים לב ש $w=w-z+z=a+b$ ולכן $|w|=|a+b|$ . כעת מאי שיוויון המשולש נקבל: $|w|=|a+b|\leq |a|+|b|=|w-z|+|z|=|z-w|+|z|$ . נעביר אגפים לקבל $|w|-|z|\leq |z-w|$ .

נאחד את שני אי-השיוויונים שקיבלנו ונקבל 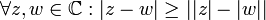$\forall z,w\in \mathbb{C}:|z-w|\geq ||z|-|w||$ .

צמוד

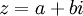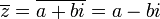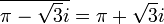לכל מספר מרוכב $z=a+bi$ נגדיר את הצמוד המרוכב שלו להיות $\overline{z}=\overline{a+bi}=a-bi$ . לדוג': $\overline{\pi-\sqrt{3}i}=\pi +\sqrt{3}i$ .

תכונות הצמוד

1. כפליות: 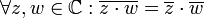$\forall z,w\in \mathbb{C}:\overline{z\cdot w}=\overline{z}\cdot \overline{w}$ .

2. חיבוריות: 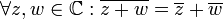$\forall z,w\in \mathbb{C}:\overline{z+ w}=\overline{z}+ \overline{w}$ .

3. אותה נורמה: 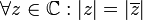$\forall z\in \mathbb{C}:|z|=|\overline{z}|$ .

ראיתם בהרצאה:

הוכיחו שלכל מספר מרוכב 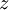$z$ מתקיים:

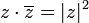1. $z\cdot \overline{z}=|z|^2$ .

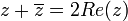2. $z+\overline{z}=2Re(z)$ .

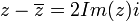
3. $z-\overline{z}=2Im(z)i$

פתרון: נסמן 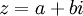$z=a+bi$ ונחשב:

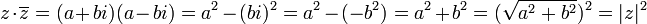$z\cdot \overline{z}=(a+bi)(a-bi)=a^2-(bi)^2=a^2-(-b^2)=a^2+b^2=(\sqrt{a^2+b^2})^2=|z|^2$ .

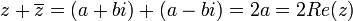$z+\overline{z}=(a+bi)+(a-bi)=2a=2Re(z)$ .

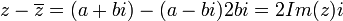
$z-\overline{z}=(a+bi)-(a-bi)2bi=2Im(z)i$

תרגיל

מצאו מספר מרוכב 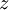$z$ המקיים: 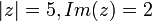$|z|=5,Im(z)=2$ , ומקמו אותו על במישור המרוכב.

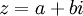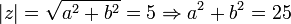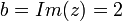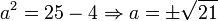פתרון: נסמן $z=a+bi$ , לכן $|z|=\sqrt{a^2+b^2}=5\Rightarrow a^2+b^2=25$ . בנוסף, $b=Im(z)=2$ , ולכן $a^2=25-4\Rightarrow a=\pm \sqrt{21}$ .

מציאת הופכי וחילוק

עובדה: לכל מספר מרוכב שונה מאפס קיים הופכי.

ש: איך נמצא את ההופכי?

ת: כמסקנה מהתרגיל האחרון המקשר בן נורמה לצמוד נקבל: 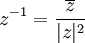$z^{-1}=\frac{\overline{z}}{|z|^2}$ .

תרגיל

מצא את ההופכי של:

1. $7-4i$

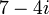
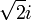
2. $\sqrt{2}i$

פתרון

1. לפי המסקנה נקבל: 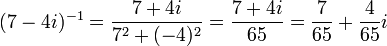$(7-4i)^{-1}=\frac{7+4i}{7^2+(-4)^2}=\frac{7+4i}{65}=\frac{7}{65}+\frac{4}{65} i$ .

2. עיבוד הנוסחה נכשל (שגיאת תחביר): (\sqrt{2}i)^{-1}=\frac{\overline{\sqrt{2}i}}{|\sqrt{2}i|=\frac{-\sqrt{2}i}{2}=-\frac{\sqrt{2}}{2} i

תרגיל

הצג את הביטוי הבא בצורה 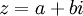$z=a+bi$ וציין מהם 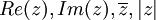$Re(z),Im(z),\overline{z},|z|$ . הביטוי הינו: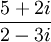 $\frac{5+2i}{2-3i}$

פתרון: נכפול בצמוד למכנה למעלה ולמטה 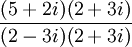$\frac{(5+2i)(2+3i)}{(2-3i)(2+3i)}$ .

נעצור לרגע להבין את הפורמליות של מה שאנחנו עושים. הרי 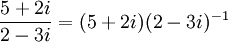$\frac{5+2i}{2-3i}=(5+2i)(2-3i)^{-1}$ וכעת רשמנו $(5+2i)(2+3i)[(2-3i)^{-1}(2+3i)^{-1}]$

לפיכך נקבל:

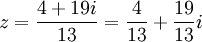$z=\frac{4+19i}{13}=\frac{4}{13}+\frac{19}{13}i$ .

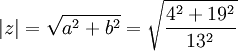$|z|=\sqrt{a^2+b^2}=\sqrt{\frac{4^2+19^2}{13^2}}$ .

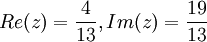$Re(z)=\frac{4}{13},Im(z)=\frac{19}{13}$ .

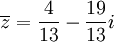$\overline{z}=\frac{4}{13}-\frac{19}{13}i$ .

תרגילים

תרגיל

פתור את המשוואה הבאה:

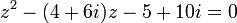1. $z^2-(4+6i)z-5+10i=0$ .

פתרון

נפתור לפי נוסחת השורשים הרגילה:

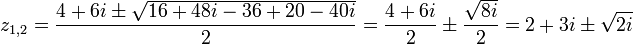$z_{1,2}=\frac{4+6i\pm \sqrt{16+48i-36+20-40i}}{2}=\frac{4+6i}{2}\pm \frac{\sqrt{8i}}{2}=2+3i\pm \sqrt{2i}$ . אבל איך מוציאים שורש למספר מרוכב? לכל מספר מרוכב קיים שורש מרוכב. נסמן אותו 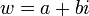$w=a+bi$ , כלומר, 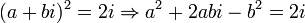$(a+bi)^2=2i\Rightarrow a^2+2abi-b^2=2i$ . נעשה השוואת מקדמים, אלה שעם 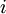$i$ ואלה שבלי ונקבל שתי משוואות בשני נעלמים:

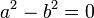
$a^2-b^2=0$

$2ab=2$ .

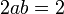מהמשוואה השנייה נקבל 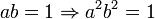$ab=1\Rightarrow a^2b^2=1$ , ולכן לפי המשוואה הראשונה נקבל 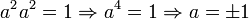$a^2a^2=1\Rightarrow a^4=1\Rightarrow a=\pm 1$ . קיבלנו שני פתרונות:

עיבוד הנוסחה נכשל (פונקציה \Rightarro לא מוכרת): a=1\Rightarrow b=1\Rightarro w=1+i

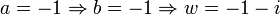$a=-1\Rightarrow b=-1\Rightarrow w=-1-i$ .

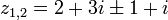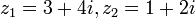בסה"כ נקבל $z_{1,2}=2+3i\pm 1+i$ , ולכן בסה"כ: $z_1=3+4i,z_2=1+2i$ .

תרגיל

א. פתרו את הנשוואה 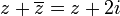$z+\overline{z}=z+2i$ .

ב. הוכיחו שלמשוואה 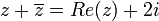$z+\overline{z}=Re(z)+2i$ אין פתרון.

פתרון: נסמן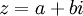 $z=a+bi$ , וניזכר שמתקיים 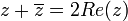$z+\overline{z}=2Re(z)$ , ונקבל 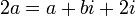$2a=a+bi+2i$ . נעשה השוואת מקדמים ונקבל:

$2a=a$

$0=b+2$ .

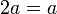
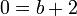לכן 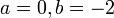$a=0,b=-2$ , כלומר, $z=-2i$ .

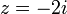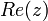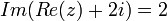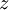ב. נשים לב שאגף ימין הוא מספר ממשי, כי $Re(z)$ תמיד ממשי. מאידך, בדיוק מאותה סיבה לצד ימין יש חלק מדומה $Im(Re(z)+2i)=2$ לכל מספר מרוכב $z$ .

@@ שורה 102: / שורה 102: @@
 ====תרגיל====
-מצא את ההופכי של <math>7-4i</math>.
+מצא את ההופכי של:
-'''פתרון:''' לפי המסקנה נקבל: <math>(7-4i)^{-1}=\frac{7+4i}{7^2+(-4)^2}=\frac{7+4i}{65}=\frac{7}{65}+\frac{4}{65} i</math>.
+. <math>7-4i</math>
+. <math>\sqrt{2}i</math>
+=====פתרון=====
+. לפי המסקנה נקבל: <math>(7-4i)^{-1}=\frac{7+4i}{7^2+(-4)^2}=\frac{7+4i}{65}=\frac{7}{65}+\frac{4}{65} i</math>.
+. <math>(\sqrt{2}i)^{-1}=\frac{\overline{\sqrt{2}i}}{|\sqrt{2}i|=\frac{-\sqrt{2}i}{2}=-\frac{\sqrt{2}}{2} i</math>
 ====תרגיל====

הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 1"

גרסה מ־09:50, 15 באוקטובר 2018

תוכן עניינים

הגדרה

חלק ממשי וחלק מדומה

נורמה וצמוד

נורמה

תכונות הנורמה

אש"מ ההפוך - בהרצאה

צמוד

תכונות הצמוד

ראיתם בהרצאה:

תרגיל

מציאת הופכי וחילוק

תרגיל

פתרון

תרגיל

תרגילים

תרגיל

פתרון

תרגיל

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים