הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 1"
מתוך Math-Wiki
(יצירת דף עם התוכן "כידוע אין שורש ממשי למספר <math>-1</math>. כלומר <math>\sqrt{-1}\notin \mathbb{R}</math>. בתחילת הקורס נלמד על מבנ...") |
|||
| שורה 3: | שורה 3: | ||
בתחילת הקורס נלמד על מבנה מתמטי בו יש שורש ל <math>-1</math>: שדה המספרים המרוכבים! | בתחילת הקורס נלמד על מבנה מתמטי בו יש שורש ל <math>-1</math>: שדה המספרים המרוכבים! | ||
| − | אז מי הם בעצם המספרים המרוכבים? נסמן <math>i=\sqrt{-1}</math> | + | אז מי הם בעצם המספרים המרוכבים? בעצם מה שאנחנו צריכים להגדיר כאן זה שלושה דברים: |
| + | |||
| + | 1. האיברים עצמם - המספרים המרוכבים. | ||
| + | |||
| + | 2. איך לחבר ביניהם. | ||
| + | |||
| + | 3. איך להכפיל ביניהם. | ||
| + | |||
| + | נסמן ב <math>i</math> איבר מסויים, ונגדיר <math>i\cdot i=-1</math>. במילים אחרות <math>i=\sqrt{-1}</math>. המספרים המרוכבים הם כל המספרים מהצורה <math>a+bi</math> כאשר <math>a,b\in \mathbb{R}</math>. כלומר, <math>\mathbb{C}=\{a+bi|a,b\in \mathbb{R}\}</math>. שימו לב שכמובן שהמספרים הממשיים מוכלים במרוכבים, פשוט לוקחים <math>b=0</math>. | ||
| + | |||
| + | חיבור: <math>(a+bi)+(x+yi):=(a+x)+(b+y)i</math>. | ||
| + | |||
| + | כפל: <math>(a+bi)\cdot (x+yi):=(ax-by)+(ay+bx)i</math>. | ||
| + | |||
| + | לדוגמא: נסמן <math>z=5+\frac{1}{3}i,w=2+\frac{2}{3}i</math>. נקבל <math>z+w=(5+2)+(\frac{1}{3}+\frac{2}{3})i=7+i</math>, וכן <math>z\cdot w=(5\cdot 2-\frac{1}{3\cdot \frac{2}{3})+(5\cdot \frac{2}{3}+\frac{1}{3}\cdot 2)i=9\frac{2}{9}+4i</math>. | ||
גרסה מ־13:22, 8 באוקטובר 2018
כידוע אין שורש ממשי למספר 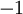 . כלומר
. כלומר 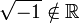 .
.
בתחילת הקורס נלמד על מבנה מתמטי בו יש שורש ל 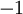 : שדה המספרים המרוכבים!
: שדה המספרים המרוכבים!
אז מי הם בעצם המספרים המרוכבים? בעצם מה שאנחנו צריכים להגדיר כאן זה שלושה דברים:
1. האיברים עצמם - המספרים המרוכבים.
2. איך לחבר ביניהם.
3. איך להכפיל ביניהם.
נסמן ב 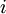 איבר מסויים, ונגדיר
איבר מסויים, ונגדיר 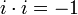 . במילים אחרות
. במילים אחרות 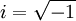 . המספרים המרוכבים הם כל המספרים מהצורה
. המספרים המרוכבים הם כל המספרים מהצורה 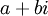 כאשר
כאשר 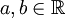 . כלומר,
. כלומר, 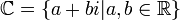 . שימו לב שכמובן שהמספרים הממשיים מוכלים במרוכבים, פשוט לוקחים
. שימו לב שכמובן שהמספרים הממשיים מוכלים במרוכבים, פשוט לוקחים 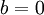 .
.
חיבור: 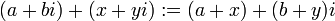 .
.
כפל: 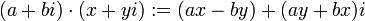 .
.
לדוגמא: נסמן 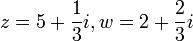 . נקבל
. נקבל 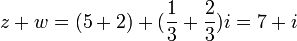 , וכן עיבוד הנוסחה נכשל (שגיאת תחביר): z\cdot w=(5\cdot 2-\frac{1}{3\cdot \frac{2}{3})+(5\cdot \frac{2}{3}+\frac{1}{3}\cdot 2)i=9\frac{2}{9}+4i
.
, וכן עיבוד הנוסחה נכשל (שגיאת תחביר): z\cdot w=(5\cdot 2-\frac{1}{3\cdot \frac{2}{3})+(5\cdot \frac{2}{3}+\frac{1}{3}\cdot 2)i=9\frac{2}{9}+4i
.