הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 1"

גרסה מ־08:41, 9 באוקטובר 2018

הגדרה

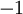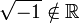כידוע אין שורש ממשי למספר $-1$ . כלומר $\sqrt{-1}\notin \mathbb{R}$ .

בתחילת הקורס נלמד על מבנה מתמטי בו יש שורש ל 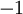$-1$ : שדה המספרים המרוכבים!

אז מי הם בעצם המספרים המרוכבים? בעצם מה שאנחנו צריכים להגדיר כאן זה שלושה דברים:

1. האיברים עצמם - המספרים המרוכבים.

2. איך לחבר ביניהם.

3. איך להכפיל ביניהם.

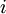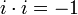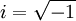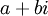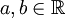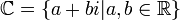נסמן ב $i$ איבר מסויים, ונגדיר $i\cdot i=-1$ . במילים אחרות $i=\sqrt{-1}$ . המספרים המרוכבים הם כל המספרים מהצורה $a+bi$ כאשר $a,b\in \mathbb{R}$ . כלומר, $\mathbb{C}=\{a+bi|a,b\in \mathbb{R}\}$ . שימו לב שכמובן שהמספרים הממשיים מוכלים במרוכבים, פשוט לוקחים $b=0$ .

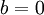חיבור: 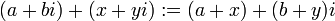$(a+bi)+(x+yi):=(a+x)+(b+y)i$ .

כפל: 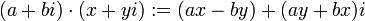$(a+bi)\cdot (x+yi):=(ax-by)+(ay+bx)i$ .

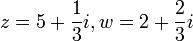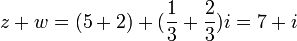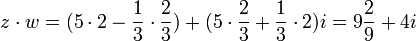לדוגמא: נסמן $z=5+\frac{1}{3}i,w=2+\frac{2}{3}i$ . נקבל: $z+w=(5+2)+(\frac{1}{3}+\frac{2}{3})i=7+i$ , וכן $z\cdot w=(5\cdot 2-\frac{1}{3}\cdot \frac{2}{3})+(5\cdot \frac{2}{3}+\frac{1}{3}\cdot 2)i=9\frac{2}{9}+4i$ .

נורמה

במספרים הממשיים יש לנו ערך מוחלט, והוא מוגדר כמרחק של המספר מאפס. נגדיר משהו דומה על המספרים המרוכבים - הנורמה (ויש שקוראים לזה ערך מוחלט). הנורמה זו בעצם פונקציה 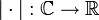$|\cdot |:\mathbb{C}\to \mathbb{R}$ המוגדרת ע"י: 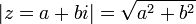$|z=a+bi|=\sqrt{a^2+b^2}$ . מאיפה הגיעה הפונקציה הזו? אם נתבונן על המספרים המרוכבים במערכת צירים נוכל לשים לב שהנורמה היא המרחק (האוקלידי) מראשית הצירים. דוגמאות נחמדות כיד המתרגל הטובה עליו.

תכונות הנורמה

1. כפליות: 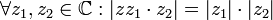$\forall z_1,z_2\in \mathbb{C}:|zz_1\cdot z_2|=|z_1|\cdot |z_2|$ .

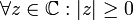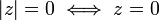2. אי שליליות: $\forall z\in \mathbb{C}:|z|\geq 0$ , ומתקיים: $|z|=0\iff z=0$ .

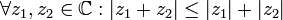3. אי שיוויון המשולש: $\forall z_1,z_2\in \mathbb{C}:|z_1+z_2|\leq |z_1|+|z_2|$ .

גרסה מ־08:39, 9 באוקטובר 2018 (הצגת מקור) אריאל (שיחה \| תרומות) (←‏תכונות הנורמה) → מעבר להשוואת הגרסאות הקודמת		גרסה מ־08:41, 9 באוקטובר 2018 (הצגת מקור) אריאל (שיחה \| תרומות) (←‏תכונות הנורמה) מעבר להשוואת הגרסאות הבאה ←
שורה 33:		שורה 33:
	2. אי שליליות: <math>\forall z\in \mathbb{C}:\|z\|\geq 0</math>, ומתקיים: <math>\|z\|=0\iff z=0</math>.		2. אי שליליות: <math>\forall z\in \mathbb{C}:\|z\|\geq 0</math>, ומתקיים: <math>\|z\|=0\iff z=0</math>.

−	3. אי שיוויון המשולש: <math>\forall z_1,z_2\in \mathbb{C}:\|z_1+z_2\|\~~seq~~ \|z_1\|+\|z_2\|</math>.	+	3. אי שיוויון המשולש: <math>\forall z_1,z_2\in \mathbb{C}:\|z_1+z_2\|\leq \|z_1\|+\|z_2\|</math>.

הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 1"

גרסה מ־08:41, 9 באוקטובר 2018

הגדרה

נורמה

תכונות הנורמה

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים