הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 4"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏גזירות)
שורה 1: שורה 1:
 
חזרה ל[[מערכי תרגול באנליזה מתקדמת למורים | מערכי תרגול]].
 
חזרה ל[[מערכי תרגול באנליזה מתקדמת למורים | מערכי תרגול]].
  
−
==הגדרה==
+
==פונקציות==
−
כדי להבין פנקציות מהצורה <math>f:\mathbb{C}\to \mathbb{C}</math> צריך להבין מה עושה פונקציה <math>f:\mathbb{R}^2\to \mathbb{R}</math>. פנקציה כזו מקבלת שני ממשיים ומוציאה ממשי אחד.
+
ראיתם כמה דוגמאות לפונקציות <math>f:\mathbb{C}\to \mathbb{C}</math>, כמו למשל <math>f(z)=Re(z)</math> וכדו'.
 +
 
 +
הרבה פעמים, כדי להבין פנקציות מהצורה <math>f:\mathbb{C}\to \mathbb{C}</math> צריך להבין מה עושה פונקציה <math>f:\mathbb{R}^2\to \mathbb{R}</math>. פנקציה כזו מקבלת שני ממשיים ומוציאה ממשי אחד.
  
 
לדוג': <math>f(x,y)=\sin(x+y)-x</math> ועוד כהנה וכהנה.
 
לדוג': <math>f(x,y)=\sin(x+y)-x</math> ועוד כהנה וכהנה.
שורה 10: שורה 12:
 
==רציפות==
 
==רציפות==
 
הגדרת רציפות של פונקציה מרוכבת: הפונקציה <math>f:\mathbb{C}\to \mathbb{C}</math> רציפה ב<math>z_0</math> אם לכל סדרה <math>z_n\to z_0</math> מתקיים: <math>|f(z_n)-f(z_0)|\to 0</math>. פונקציה נקראת רציפה אם היא רציפה בכל נקודה.
 
הגדרת רציפות של פונקציה מרוכבת: הפונקציה <math>f:\mathbb{C}\to \mathbb{C}</math> רציפה ב<math>z_0</math> אם לכל סדרה <math>z_n\to z_0</math> מתקיים: <math>|f(z_n)-f(z_0)|\to 0</math>. פונקציה נקראת רציפה אם היא רציפה בכל נקודה.
 +
 +
====תרגיל====
 +
הוכיחו שהפונקציה <math>f(z)=\overline{z}</math> היא רציפה.
 +
 +
=====פתרון=====
 +
לפי הגדרה: תהי <math>z_n\to z</math>, צריך להראות ש- <math>|f(z_n)-f(z)|\to 0</math>. ואכן: <math>|f(z_n)-f(z)|=|\overline{z_n}-\overline{z}|=|\overline{z_n-z}|=|z_n-z|\to 0</math>, כאשר השאיפה בסוף נובעת מהנתון על הסדרה.
  
 
===משפטים===
 
===משפטים===
−
כרגיל, לא תמיד משתמשים בהגדרה, אלא במשפטים. המשפטים הרגילים: חיבור, כפל, הרכבה וחילוק כשמותר של רציפות זו פונקציה רציפה. לכן כל הפולינומים רציפים, וכנ"ל מנת פולינומים (מה שנקרא פונקציה רציונאלית) כשהמכנה לא 0.
+
כרגיל, לא תמיד משתמשים בהגדרה, אלא במשפטים. המשפטים הרגילים: חיבור, כפל, הרכבה וחילוק כשמותר (כלומר, כשהמכנה לא אפס) של פונקציות רציפות זו פונקציה רציפה. לכן כל הפולינומים רציפים, וכנ"ל מנת פולינומים (מה שנקרא פונקציה רציונאלית) כשהמכנה לא 0.
  
 
משפט חשוב: <math>f(a+bi)=U(a,b)+iV(a,b)</math> רציפה אם ורק אם <math>U,V</math> רציפות.
 
משפט חשוב: <math>f(a+bi)=U(a,b)+iV(a,b)</math> רציפה אם ורק אם <math>U,V</math> רציפות.
−
 
−
לכן, חשוב להבין רציפות של פונקציות בשתי משתנים.
 
  
 
===רציפות של פונקציות בשני משתנים===
 
===רציפות של פונקציות בשני משתנים===
שורה 22: שורה 28:
  
 
====תרגיל====
 
====תרגיל====
 +
האם הפונקציות הבאות רציפות:
  
−
האם הפונקציה הבאה רציפה בראשית הצירים: <math>f(x,y)=\begin{cases}
+
1. <math>f(z)=\frac{z+2\overline{z}}{z\overline{z}+2}</math>
−
\frac{\sin x}{y} & y\neq0\\
+
−
1 & y=0
+
−
\end{cases}</math>
+
  
−
אם לא, האם ניתן להגדיר אחרת ב<math>(0,0)</math> כדי שכן תהיה רציפה שם?
+
2. <math>f(z)=Im(z)-Re(z)i</math>
−
=====פתרון=====
+
−
לא ולא! על מנת להראות שהפונקציה לא רציפה מספיק למצוא זוג אחד של סדרות <math>x_{n}\to 0,y_{n}\to 0</math> עבורן לא מתקיים: <math>|f(x_{n},y_{n})-f(0,0)|\to 0</math>. וזה מה שנעשה כאן:
+
  
−
אם נקבע את סדרת האיקסים להיות תמיד אפס, כלומר, <math>x_{n}=0</math>, וניקח למשל <math>y_{n}=\frac{1}{n}</math>, אז נקבל סדרת אפסים (כי המונה תמיד אפס), ולכן הגבול גם הוא אפס (הסדרה היא <math>f(x_{n},y_{n})=\frac{\sin0}{\frac{1}{n}}=0</math>). כיון שהגבול שונה מערך הפונקציה ב<math>(0,0)</math> נובע שהפונקציה לא רציפה.
+
3. <math>f(z)=\frac{z^2-2z+1}{z^2+1}</math>
  
−
הערה חשובה: לא ניתן "לתקן" ע"י לקבוע <math>f(0,0)=0</math> כי אם ניקח את הסדרות <math>x_{n}=y_{n}=\frac{1}{n}</math> נקבל <math>f(x_{n},y_{n})=\frac{\sin\frac{1}{n}}{\frac{1}{n}}\to 1</math> לפי הידוע משנה שעברה, וכיון שיש שני גבולות שונים נובע שאין דרך "לתקן".
+
4. <math>f(x+yi)=\frac{\sin x}{x}-\frac{\cos x}{x}i</math>
  
−
====תרגיל====
+
5. <math>f(x+yi)=e^x(\sin y+i\tan y)</math>
  
−
האם הפונקציה הבאה רציפה בראשית הצירים: <math>f(x,y)=\begin{cases}
+
6. <math>f(x+yi)=\frac{\sin(xy)}{|y|=5}-x\text{cis}y</math>
−
\frac{\sin(x\cdot y)}{x} & x\neq0\\
+
−
0 & x=0
+
−
\end{cases}</math>
+
  
 
=====פתרון=====
 
=====פתרון=====
−
 
−
אכן כן. נלך לפי הגדרה: צריך להראות שלכל שתי סדרות <math>x_{n},y_{n}</math> מתקיים: <math>|f(x_{n},y_{n})-f(0,0)|\to 0</math>. נראה זאת:
 
−
 
−
<math>|f(x_{n},y_{n})-f(0,0)|=|\frac{\sin(x_{n}y_{n})}{x_{n}}|=\frac{|\sin(x_{n}y_{n})|}{|x_{n}|}</math>. עכשיו נשתמש ברמז שכתוב: תמיד מתקיים <math>|\sin x|\leq|x|</math>, ולכן אצלנו נקבל <math>|\sin(xy)|\leq|xy|</math> ונוכל להמשיך:
 
−
 
−
<math>\frac{|\sin(x_{n}y_{n})|}{|x_{n}|}\leq\frac{|x_{n}y_{n}|}{|x_{n}|}=\frac{|x_{n}|\cdot|y_{n}|}{|x_{n}|}=|y_{n}|\to 0</math>
 
−
 
−
===רציפות של פונקציות מרוכבות===
 
−
====תרגיל====
 
−
האם הפונקציות הבאות רציפות בנקודות הנדרשות:
 
−
 
−
1.<math>f(z)=\frac{z^2-2z+1}{z^2+1}</math> בכל <math>\mathbb{C}\smallsetminus \{i,-i\}</math>.
 
−
 
−
2. <math>f(z)=\begin{cases} \frac{3z+\overline{z}}{2z-\overline{z}} & z\neq 0 \\ \frac{2}{10} & z=0 \end{cases}</math> ב<math>z=0</math>.
 
−
 
−
=====פתרון=====
 
−
1. כן, פונקציה רציונאלית רציפה כאשר המכנה לא מתאפס.
 
−
 
−
2. לא! נקבל:
 
−
 
−
<math>f(a+bi)=\frac{3a+3bi+a-bi}{2a+2bi-a+bi}=\dots =\frac{4a^2+6b^2}{9b^2+a^2}-\frac{6ab}{9b^2+a^2}i</math>.
 
−
 
−
כעת, "קל לראות" שהפונקציה שתמונתה החלק המדומה לא רציפה. ניקח סדרות <math>a_n=b_n,a_n=-b_n</math>.
 

גרסה מ־11:40, 10 בדצמבר 2019

חזרה ל מערכי תרגול.

פונקציות

ראיתם כמה דוגמאות לפונקציות 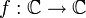f:\mathbb{C}\to \mathbb{C}, כמו למשל 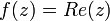f(z)=Re(z) וכדו'.

הרבה פעמים, כדי להבין פנקציות מהצורה 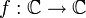f:\mathbb{C}\to \mathbb{C} צריך להבין מה עושה פונקציה 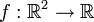f:\mathbb{R}^2\to \mathbb{R}. פנקציה כזו מקבלת שני ממשיים ומוציאה ממשי אחד.

לדוג': 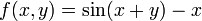f(x,y)=\sin(x+y)-x ועוד כהנה וכהנה.

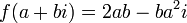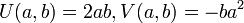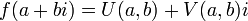במרוכבים זה יופיע כשתי פונקציות כאלה. למשל, נניח שיש לנו את הפונקציה f(a+bi)=2ab-ba^2i, זה בעצם חיבור של שתי הפונקציות הבאות: U(a,b)=2ab,V(a,b)=-ba^2 ואז נקבל: f(a+bi)=U(a,b)+V(a,b)i.

רציפות

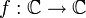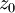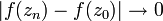הגדרת רציפות של פונקציה מרוכבת: הפונקציה f:\mathbb{C}\to \mathbb{C} רציפה בz_0 אם לכל סדרה z_n\to z_0 מתקיים: |f(z_n)-f(z_0)|\to 0. פונקציה נקראת רציפה אם היא רציפה בכל נקודה.

תרגיל

הוכיחו שהפונקציה 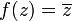f(z)=\overline{z} היא רציפה.

פתרון

לפי הגדרה: תהי 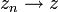z_n\to z, צריך להראות ש- 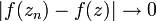|f(z_n)-f(z)|\to 0. ואכן: 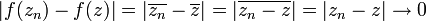|f(z_n)-f(z)|=|\overline{z_n}-\overline{z}|=|\overline{z_n-z}|=|z_n-z|\to 0, כאשר השאיפה בסוף נובעת מהנתון על הסדרה.

משפטים

כרגיל, לא תמיד משתמשים בהגדרה, אלא במשפטים. המשפטים הרגילים: חיבור, כפל, הרכבה וחילוק כשמותר (כלומר, כשהמכנה לא אפס) של פונקציות רציפות זו פונקציה רציפה. לכן כל הפולינומים רציפים, וכנ"ל מנת פולינומים (מה שנקרא פונקציה רציונאלית) כשהמכנה לא 0.

משפט חשוב: 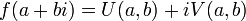f(a+bi)=U(a,b)+iV(a,b) רציפה אם ורק אם 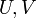U,V רציפות.

רציפות של פונקציות בשני משתנים

פונקציה 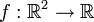f:\mathbb{R}^2\to \mathbb{R} רציפה בנק' 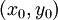(x_0,y_0) אם לכל זוג סדרות 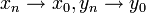x_n\to x_0,y_n\to y_0 מתקיים: 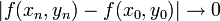|f(x_n,y_n)-f(x_0,y_0)|\to 0. כדי להראות שהפונקציה לא רציפה מספיק למצוא זוג אחד של סדרות שלא מקיימות את התנאי.

תרגיל

האם הפונקציות הבאות רציפות:

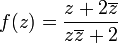
1. f(z)=\frac{z+2\overline{z}}{z\overline{z}+2}

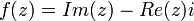
2. f(z)=Im(z)-Re(z)i

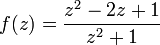
3. f(z)=\frac{z^2-2z+1}{z^2+1}

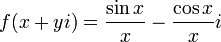
4. f(x+yi)=\frac{\sin x}{x}-\frac{\cos x}{x}i

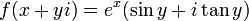
5. f(x+yi)=e^x(\sin y+i\tan y)

6. f(x+yi)=\frac{\sin(xy)}{|y|=5}-x\text{cis}y

פתרון
מקור: https://math-wiki.com/index.php?title=אנליזה_מתקדמת_למורים_תרגול_4&oldid=82951