אנליזה מתקדמת למורים תרגול 4
חזרה ל מערכי תרגול.
תוכן עניינים
הגדרה
כדי להבין פנקציות מהצורה 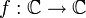 צריך להבין מה עושה פונקציה
צריך להבין מה עושה פונקציה 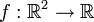 . פנקציה כזו מקבלת שני ממשיים ומוציאה ממשי אחד.
. פנקציה כזו מקבלת שני ממשיים ומוציאה ממשי אחד.
לדוג': 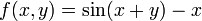 ועוד כהנה וכהנה.
ועוד כהנה וכהנה.
במרוכבים זה יופיע כשתי פונקציות כאלה. למשל, נניח שיש לנו את הפונקציה 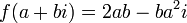 , זה בעצם חיבור של שתי הפונקציות הבאות:
, זה בעצם חיבור של שתי הפונקציות הבאות: 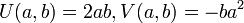 ואז נקבל:
ואז נקבל: 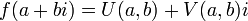 .
.
רציפות
הגדרת רציפות של פונקציה מרוכבת: הפונקציה 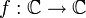 רציפה ב
רציפה ב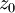 אם לכל סדרה
אם לכל סדרה  מתקיים:
מתקיים: 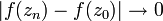 . פונקציה נקראת רציפה אם היא רציפה בכל נקודה.
. פונקציה נקראת רציפה אם היא רציפה בכל נקודה.
משפטים
כרגיל, לא תמיד משתמשים בהגדרה, אלא במשפטים. המשפטים הרגילים: חיבור, כפל, הרכבה וחילוק כשמותר של רציפות זו פונקציה רציפה. לכן כל הפולינומים רציפים, וכנ"ל מנת פולינומים (מה שנקרא פונקציה רציונאלית) כשהמכנה לא 0.
משפט חשוב: 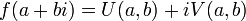 רציפה אם ורק אם
רציפה אם ורק אם 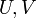 רציפות.
רציפות.
לכן, חשוב להבין רציפות של פונקציות בשתי משתנים.
רציפות של פונקציות בשני משתנים
פונקציה 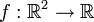 רציפה בנק'
רציפה בנק' 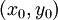 אם לכל זוג סדרות
אם לכל זוג סדרות 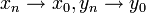 מתקיים:
מתקיים: 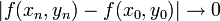 . כדי להראות שהפונקציה לא רציפה מספיק למצוא זוג אחד של סדרות שלא מקיימות את התנאי.
. כדי להראות שהפונקציה לא רציפה מספיק למצוא זוג אחד של סדרות שלא מקיימות את התנאי.
תרגיל
האם הפונקציה הבאה רציפה בראשית הצירים: 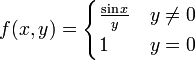
אם לא, האם ניתן להגדיר אחרת ב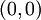 כדי שכן תהיה רציפה שם?
כדי שכן תהיה רציפה שם?
פתרון
לא ולא! על מנת להראות שהפונקציה לא רציפה מספיק למצוא זוג אחד של סדרות 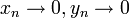 עבורן לא מתקיים:
עבורן לא מתקיים: 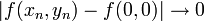 . וזה מה שנעשה כאן:
. וזה מה שנעשה כאן:
אם נקבע את סדרת האיקסים להיות תמיד אפס, כלומר, 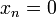 , וניקח למשל
, וניקח למשל 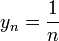 , אז נקבל סדרת אפסים (כי המונה תמיד אפס), ולכן הגבול גם הוא אפס (הסדרה היא
, אז נקבל סדרת אפסים (כי המונה תמיד אפס), ולכן הגבול גם הוא אפס (הסדרה היא 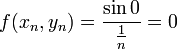 ). כיון שהגבול שונה מערך הפונקציה ב
). כיון שהגבול שונה מערך הפונקציה ב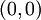 נובע שהפונקציה לא רציפה.
נובע שהפונקציה לא רציפה.
הערה חשובה: לא ניתן "לתקן" ע"י לקבוע  כי אם ניקח את הסדרות
כי אם ניקח את הסדרות 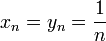 נקבל
נקבל 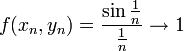 לפי הידוע משנה שעברה, וכיון שיש שני גבולות שונים נובע שאין דרך "לתקן".
לפי הידוע משנה שעברה, וכיון שיש שני גבולות שונים נובע שאין דרך "לתקן".