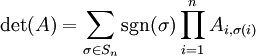דטרמיננטה לפי תמורות
הדטרמיננטה של מטריצה בגודל 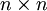 מוגדרת על-פי הנוסחה הבאה:
מוגדרת על-פי הנוסחה הבאה:
הסכום בנוסחה הוא על 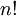 התמורות
התמורות  האפשריות של המספרים
האפשריות של המספרים 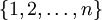 . הסימן
. הסימן 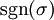 מתקבל על פי זוגיות התמורה. אם התמורה זוגית,
מתקבל על פי זוגיות התמורה. אם התמורה זוגית, 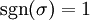 , אם היא אי זוגית,
, אם היא אי זוגית, 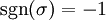 .
.
מעשית: עושים 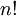 סכומים על כל הצורות (סידורים) האפשריות של הכפלת n איברים לפי התאמה חד חד ערכית בין קבוצת (אינדקס) השורות לקבוצת (אינדקס) העמודות. מקדם התמורה יקבע לפי מספר האיברים בסידור שלגביהם מספר (אינדקס) השורה גדול ממספר העמודה, אם המספר זוגי המקדם יהיה +, ואם אי זוגי הוא יהיה -.
סכומים על כל הצורות (סידורים) האפשריות של הכפלת n איברים לפי התאמה חד חד ערכית בין קבוצת (אינדקס) השורות לקבוצת (אינדקס) העמודות. מקדם התמורה יקבע לפי מספר האיברים בסידור שלגביהם מספר (אינדקס) השורה גדול ממספר העמודה, אם המספר זוגי המקדם יהיה +, ואם אי זוגי הוא יהיה -.
לדוגמה: אם יש לנו מטריצה כזאת:
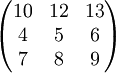
אזי התמורות האפשריות הם כך(עבור כל שורה ושורה בנפרד, המספרים כאן מייצגים את העמודות כלומר J):
(*) 1->2->3
1->2 3->3
1->3 2->2
1->3->2
1->1 2->2 3->3
1->1 2->3 עבור השורה הראשונה וכך גם לשאר השורות.
ניקח דוגמה לתמורה כלשהי: נניח שהתמורה שלנו היא התמורה בשורה הראשונה,ועוד נניח שכעת אנו נמצאים בתמורה כמו השורה הראשונה(*), לכן עבור אינדקס של J =1 יהיה לנו 12, כי הסיגמה על 1 נותן לנו את העמודה השניה, אם היה לנו J=2 היינו מקבלים 13 כי הסיגמה עליו נותנת את העמודה השלישית. ואז עושים אותו הדבר בשורה השניה והשלישית, והדטרמיננטה יוצאת מה שהיא יוצאת לפי הנוסחה.