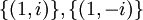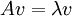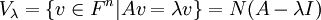וקטור עצמי
תוכן עניינים
הגדרה
יהי שדה F, ותהי 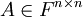 מטריצה ריבועית מעל השדה
מטריצה ריבועית מעל השדה
יהיו 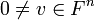 ו-
ו-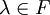 כך ש:
כך ש:
אזי v נקרא וקטור עצמי (ו"ע) של המטריצה A ו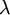 הוא הערך העצמי (ע"ע) המתאים לו.
הוא הערך העצמי (ע"ע) המתאים לו.
חישוב ע"ע וו"ע
נביט ב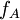 הפולינום האופייני של המטריצה A. אזי
הפולינום האופייני של המטריצה A. אזי 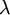 הוא ע"ע של A אם"ם
הוא ע"ע של A אם"ם 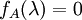 .
.
כלומר, הע"ע הם בדיוק השורשים של הפולינום האופייני, וכך נחשב אותם.
לאחר שנמצא את כל הע"ע, נמצא את הוקטורים העצמיים המתאימים להם, בעזרת חישוב המרחב העצמי:
(הזכרו בהגדרה של מרחב האפס)
דוגמאות
א
מצא את הערכים העצמיים והמרחבים העצמיים של המטריצה
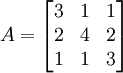
פתרון.
קודם כל נחשב את הפולינום האופייני של  :
:
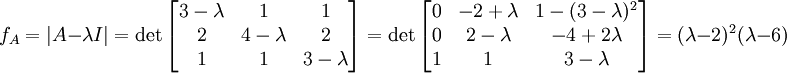
לכן הערכים העצמיים של המטריצה, הרי הם השורשים של הפולינום האופייני, הינם 2 ו6.
כעת אנו צריכים למצוא בסיסים למרחבים העצמיים של  .
.
המרחב העצמי של 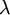 שווה למרחב הפתרונות של המערכת ההומוגנית
שווה למרחב הפתרונות של המערכת ההומוגנית 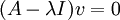 .
.
בסיס למרחב האפס 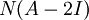 הינו
הינו 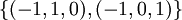 ובסיס למרחב האפס
ובסיס למרחב האפס 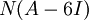 הינו
הינו 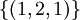 .
.
ב
מצא ע"ע וו"ע של המטריצה 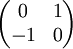 מעל הממשיים ומעל המרוכבים.
מעל הממשיים ומעל המרוכבים.
פתרון.
קל לראות כי הפולינום האופייני הינו 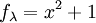 , ולכן אין ע"ע וו"ע כלל מעל הממשיים כיוון שאין שורשים לפולינום האופייני מעל הממשיים.
, ולכן אין ע"ע וו"ע כלל מעל הממשיים כיוון שאין שורשים לפולינום האופייני מעל הממשיים.
לעומת זאת, מעל המרוכבים הע"ע הינם 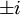 והבסיסים למרחבים העצמיים הינם
והבסיסים למרחבים העצמיים הינם