הבדלים בין גרסאות בדף "חדוא 1 - ארז שיינר"
מתוך Math-Wiki
(←חסמים) |
(←פרק 2 - סדרות) |
||
| שורה 59: | שורה 59: | ||
==פרק 2 - סדרות== | ==פרק 2 - סדרות== | ||
| + | |||
| + | *הגדרת הגבול של סדרה: | ||
| + | *תהי סדרה ממשית <math>a_n</math> ויהי מספר ממשי <math>L\in\mathbb{R}</math>. | ||
| + | *<math>L</math> הינו גבול הסדרה <math>a_n</math> (מסומן <math>\lim a_n=L</math> או <math>a_n\to L</math>) אם: | ||
| + | **לכל סביבה של הגבול, קיים מקום בסדרה שאחריו כל איברי הסדרה נמצאים בסביבה הנתונה, כלומר: | ||
| + | **לכל מרחק <math>\varepsilon>0</math> קיים מקום <math>N\in\mathbb{N}</math> כך שאחריו לכל <math>n>N</math> מתקיים כי <math>|a_n-L|<\varepsilon</math> | ||
| + | |||
| + | |||
<videoflash>mMVBYUDmSA0</videoflash> | <videoflash>mMVBYUDmSA0</videoflash> | ||
| + | |||
| + | |||
| + | *נגדיר ש<math>a_n\to\infty</math> אם לכל <math>M>0</math> קיים <math>N\in\mathbb{N}</math> כך שלכל <math>n>N</math> מתקיים כי <math>a_n>M</math> | ||
| + | *נגדיר ש<math>a_n\to -\infty</math> אם <math>-a_n\to\infty</math> | ||
| + | |||
| + | |||
| + | *טענה: תהי <math>a_n\to \infty</math> אזי <math>\frac{1}{a_n}\to 0</math> | ||
| + | *טענה: תהי <math>0\neq a_n\to 0</math> אזי <math>\frac{1}{|a_n|}\to\infty</math> | ||
| + | |||
<videoflash>U5RUHjrHVGI</videoflash> | <videoflash>U5RUHjrHVGI</videoflash> | ||
גרסה מ־12:41, 15 באוקטובר 2020
תוכן עניינים
מבחנים ופתרונות
סרטוני ותקציר ההרצאות
פרק 1 - מספרים וחסמים
קבוצות מספרים
- הטבעיים
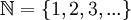
- השלמים
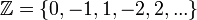
- הרציונאליים
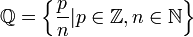
- הממשיים
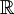 , כל השברים העשרוניים כולל האינסופיים
, כל השברים העשרוניים כולל האינסופיים
- העשרה: בנייה של שדה הממשיים באמצעות חתכי דדקינד
- לא קיים
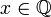 כך ש
כך ש 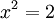 .
. - במילים פשוטות,
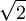 אינו רציונאלי (בהמשך נוכיח שיש מספר ממשי כזה).
אינו רציונאלי (בהמשך נוכיח שיש מספר ממשי כזה).
חסמים
- תהי
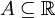 אזי:
אזי:
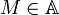 נקרא המקסימום של A או האיבר הגדול ביותר של A אם לכל
נקרא המקסימום של A או האיבר הגדול ביותר של A אם לכל 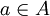 מתקיים כי
מתקיים כי 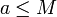
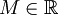 נקרא חסם מלעיל של A אם לכל
נקרא חסם מלעיל של A אם לכל 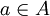 מתקיים כי
מתקיים כי 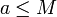
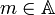 נקרא המינימום של A או האיבר הקטן ביותר של A אם לכל
נקרא המינימום של A או האיבר הקטן ביותר של A אם לכל 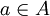 מתקיים כי
מתקיים כי 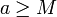
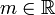 נקרא חסם מלרע של A אם לכל
נקרא חסם מלרע של A אם לכל 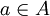 מתקיים כי
מתקיים כי 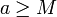
- כמו כן:
- אם יש איבר קטן ביותר בקבוצת חסמי המלעיל של A הוא נקרא החסם העליון של A, או הסופרמום של A ומסומן
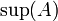
- אם יש איבר גדול ביותר בקבוצת חסמי המלרע של A הוא נקרא החסם התחתון של A, או האינפימום של A ומסומן
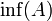
- אם יש איבר קטן ביותר בקבוצת חסמי המלעיל של A הוא נקרא החסם העליון של A, או הסופרמום של A ומסומן
- בשדה הממשיים לכל קבוצה לא ריקה וחסומה מלעיל יש חסם עליון, ולכל קבוצה לא ריקה וחסומה מלרע יש חסם תחתון.
- בשדה הרציונאליים זה לא נכון; לקבוצה
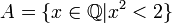 אין מספר רציונאלי קטן ביותר מבין חסמי המלעיל שלה.
אין מספר רציונאלי קטן ביותר מבין חסמי המלעיל שלה.
- תהי
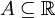 ויהי
ויהי 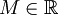 אזי:
אזי:
- M הוא החסם העליון של A אם ורק אם M הוא חסם מלעיל של A ולכל מספר
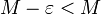 קיים מספר
קיים מספר 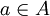 כך ש
כך ש 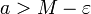
- m הוא החסם התחתון של A אם ורק אם m הוא חסם מלרע של A ולכל מספר
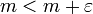 קיים מספר
קיים מספר 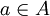 כך ש
כך ש 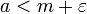
- M הוא החסם העליון של A אם ורק אם M הוא חסם מלעיל של A ולכל מספר
פרק 2 - סדרות
- הגדרת הגבול של סדרה:
- תהי סדרה ממשית
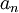 ויהי מספר ממשי
ויהי מספר ממשי 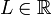 .
. 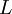 הינו גבול הסדרה
הינו גבול הסדרה 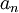 (מסומן
(מסומן 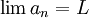 או
או 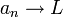 ) אם:
) אם:
- לכל סביבה של הגבול, קיים מקום בסדרה שאחריו כל איברי הסדרה נמצאים בסביבה הנתונה, כלומר:
- לכל מרחק
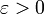 קיים מקום
קיים מקום 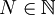 כך שאחריו לכל
כך שאחריו לכל 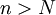 מתקיים כי
מתקיים כי 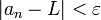
- נגדיר ש
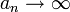 אם לכל
אם לכל 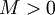 קיים
קיים 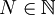 כך שלכל
כך שלכל 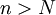 מתקיים כי
מתקיים כי 
- נגדיר ש
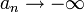 אם
אם 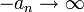
- טענה: תהי
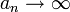 אזי
אזי 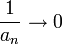
- טענה: תהי
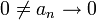 אזי
אזי 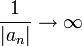
פרק 3 - טורים
פרק 4 - פונקציות ורציפות
פרק 5 - גזירות