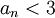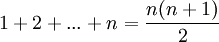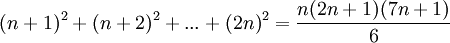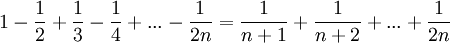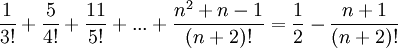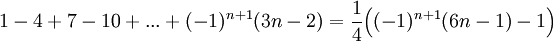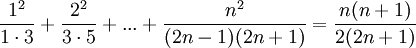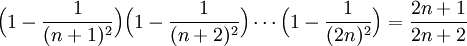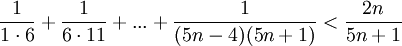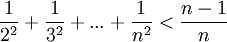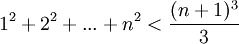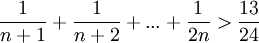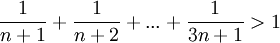הבדלים בין גרסאות בדף "מכינה למחלקת מתמטיקה/מערכי שיעור/7"
מתוך Math-Wiki
(←תרגילים) |
(←תרגילים - אי שיוויונים) |
||
| (13 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 9: | שורה 9: | ||
*כל טענה גוררת את הבאה אחריה. כלומר, לכל n אם נניח כי <math>P(n)</math> נכון, נוכל להוכיח כי <math>P(n+1)</math> נכון גם הוא | *כל טענה גוררת את הבאה אחריה. כלומר, לכל n אם נניח כי <math>P(n)</math> נכון, נוכל להוכיח כי <math>P(n+1)</math> נכון גם הוא | ||
| + | דוגמאות: | ||
| − | ==תרגילים== | + | כמות הזוגות בקבוצה מגודל n |
| + | |||
| + | טבלאת שוקולד עם n קוביות | ||
| + | |||
| + | ==תרגילים - שיוויונים== | ||
*<math>1+2+...+n=\frac{n(n+1)}{2}</math> | *<math>1+2+...+n=\frac{n(n+1)}{2}</math> | ||
| שורה 21: | שורה 26: | ||
| − | *<math>(n+1)^2+(n+2)^2+...+(2n)^2=\frac{n(2n+1)(7n+1}{6}</math> | + | *<math>(n+1)^2+(n+2)^2+...+(2n)^2=\frac{n(2n+1)(7n+1)}{6}</math> |
| + | |||
| + | |||
| + | *<math>1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...-\frac{1}{2n}=\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{2n}</math> | ||
| + | |||
| + | |||
| + | *<math>\frac{1}{3!}+\frac{5}{4!}+\frac{11}{5!}+...+\frac{n^2+n-1}{(n+2)!}=\frac{1}{2}-\frac{n+1}{(n+2)!}</math> | ||
| + | |||
| + | |||
| + | *נתבונן בסדרת פיבונאצ'י בה כל איבר שווה לסכום שני קודמיו <math>F_{n+2}=F_{n+1}+F_n</math>. הוכח כי <math>F_n=\frac{1}{\sqrt{5}}\Big((\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n\Big)</math> | ||
| + | |||
| + | |||
| + | *<math>1-4+7-10+...+(-1)^{n+1}(3n-2)=\frac{1}{4}\Big((-1)^{n+1}(6n-1)-1\Big)</math> | ||
| + | |||
| + | |||
| + | *<math>\frac{1^2}{1\cdot 3}+\frac{2^2}{3\cdot 5}+...+\frac{n^2}{(2n-1)(2n+1)}=\frac{n(n+1)}{2(2n+1)}</math> | ||
| + | |||
| + | |||
| + | *<math>\Big(1-\frac{1}{(n+1)^2}\Big)\Big(1-\frac{1}{(n+2)^2}\Big)\cdots \Big(1-\frac{1}{(2n)^2}\Big)=\frac{2n+1}{2n+2}</math> | ||
| + | |||
| + | |||
| + | ==תרגילים - אי שיוויונים== | ||
| + | |||
| + | *<math>3^n+4^n<5^n</math> לכל <math>n\geq 3</math> | ||
| + | |||
| + | |||
| + | *<math>(1+x)^n\geq 1+nx</math> לכל <math>-1<x\in\mathbb{R}</math> | ||
| + | |||
| + | |||
| + | *<math>\frac{1}{1\cdot 6}+\frac{1}{6\cdot 11} +...+\frac{1}{(5n-4)(5n+1)}<\frac{2n}{5n+1}</math> | ||
| + | |||
| + | |||
| + | *<math>\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{n^2}<\frac{n-1}{n}</math> | ||
| + | |||
| + | |||
| + | *נניח <math>a_1=2</math> וגם <math>a_{n+1}=\sqrt{6+a_n}</math>. הוכח כי <math>a_n<3</math> | ||
| + | |||
| + | |||
| + | *<math>1^2+2^2+...+n^2<\frac{(n+1)^3}{3}</math> | ||
| + | |||
| + | |||
| + | *<math>\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{2n}>\frac{13}{24}</math> | ||
| + | |||
| + | |||
| + | *<math>\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{3n+1}>1</math> | ||
גרסה אחרונה מ־13:01, 1 בספטמבר 2020
אינדוקציה מתמטית
בהנתן סדרת טענות 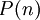 , אנו מוכיחים לפי אינדוקציה כי כל הטענות נכונות אם מתקיימים שני התנאים הבאים:
, אנו מוכיחים לפי אינדוקציה כי כל הטענות נכונות אם מתקיימים שני התנאים הבאים:
- הטענה הראשונה נכונה (כלומר, עבור n=1)
- כל טענה גוררת את הבאה אחריה. כלומר, לכל n אם נניח כי
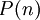 נכון, נוכל להוכיח כי
נכון, נוכל להוכיח כי 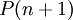 נכון גם הוא
נכון גם הוא
דוגמאות:
כמות הזוגות בקבוצה מגודל n
טבלאת שוקולד עם n קוביות
תרגילים - שיוויונים
- נתבונן בסדרת פיבונאצ'י בה כל איבר שווה לסכום שני קודמיו
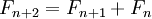 . הוכח כי
. הוכח כי 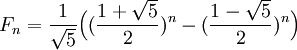
תרגילים - אי שיוויונים
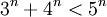 לכל
לכל 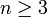
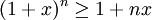 לכל
לכל 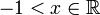
- נניח
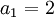 וגם
וגם 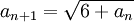 . הוכח כי
. הוכח כי