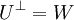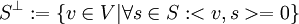הבדלים בין גרסאות בדף "מרחב ניצב"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏1)
(←‏1)
שורה 24: שורה 24:
 
ד. לכל קבוצה <math>S\subseteq V</math> מתקיים <math>\Big(span(S)\Big)^\perp = S^\perp</math>
 
ד. לכל קבוצה <math>S\subseteq V</math> מתקיים <math>\Big(span(S)\Big)^\perp = S^\perp</math>
  
 +
 +
'''פתרון:'''
 +
 +
א.
 +
 +
<math>\{0\}^\perp = \{v\in V|<v,0>=0\}=V</math>
 +
 +
 +
ב.
 +
 +
<math>V^\perp = \{w\in V|\forall v\in V:<w,v>=0\}</math>
 +
 +
אם כך, נניח <math>w\in V^\perp</math>, כיוון <math>w\in V</math> מתקיים ביחד <math><w,w>=0</math> ולפי אי שליליות <math>w=0</math>
 +
 +
לכן סה"כ <math>V^\perp=\{0\}</math>
  
 
===2===
 
===2===

גרסה מ־12:07, 25 בדצמבר 2012

הגדרה

יהי מרחב מכפלה פנימית V ותהי קבוצת וקטורים 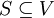S\subseteq V. אזי הקבוצה


S^\perp :=\{v\in V|\forall s\in S:<v,s>=0\}


הינה מרחב וקטורי. אנו קוראים ל 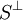S^\perp המרחב הניצב ל-S

תרגילים

משפט הפירוק הניצב

יהי V מרחב מכפלה פנימית, ויהי 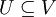U\subseteq V תת מרחב הוכיחו כי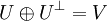 U\oplus U^\perp = V

1

יהי V מרחב מכפלה פנימית. הוכח את הטענות הבאות:

א. 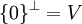\{0\}^\perp=V

ב. 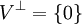V^\perp = \{0\}

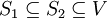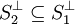
ג. אם S_1\subseteq S_2\subseteq V אזי S_2^\perp\subseteq S_1^\perp

ד. לכל קבוצה 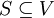S\subseteq V מתקיים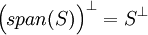 \Big(span(S)\Big)^\perp = S^\perp


פתרון:

א.

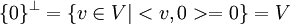
\{0\}^\perp = \{v\in V|<v,0>=0\}=V


ב.

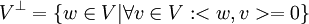
V^\perp = \{w\in V|\forall v\in V:<w,v>=0\}

אם כך, נניח 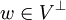w\in V^\perp, כיוון 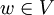w\in V מתקיים ביחד 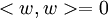<w,w>=0 ולפי אי שליליות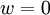 w=0

לכן סה"כ 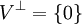V^\perp=\{0\}

2

יהי V מרחב מכפלה פנימית, ויהיו 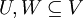U,W\subseteq V תתי מרחבים. הוכיחו/הפריכו:

א. 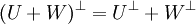(U+W)^\perp=U^\perp+W^\perp

ב.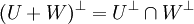(U+W)^\perp=U^\perp\cap W^\perp

ג. 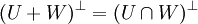(U+W)^\perp=(U\cap W)^\perp

3

יהי V מרחב מכפלה פנימית, ויהיו 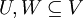U,W\subseteq V תתי מרחבים כך ש 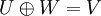U\oplus W = V. הוכיחו/הפריכו U^\perp = W

מקור: https://math-wiki.com/index.php?title=מרחב_ניצב&oldid=30357