הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/1.3.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
מ |
|||
| (2 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | {{ | + | {{המשך הגיע|תיאור=ההוכחה למשפט 11|תאריך=27.2.11}} |
=האינטגרל לפי רימן {{הערה|(המשך)}}= | =האינטגרל לפי רימן {{הערה|(המשך)}}= | ||
| שורה 10: | שורה 10: | ||
===הוכחה=== | ===הוכחה=== | ||
| − | # כיוון ש-f אינטגרבילית ב-<math>[a,b]</math> משפט 9 נותן שלכל <math>x\in[a,b]</math> f אינטגרבילית בקטע <math>[a,x_0]</math> ולכן <math>A(x)=\int\limits_a^x f</math> מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה: <math>|f(x)|\le M</math> לכל <math>x\in[a,b]</math>. כעת אם <math>x,y\in[a,b]</math> אז <math>|A(y)-A(x)|=\left|\int\limits_a^y f-\int\limits_a^x f\right|=\left|\int\limits_x^y f\right|\le M|y-x|</math> ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה <math>x_0\in[a,b]</math>. ר"ל A גזירה שם. ובכן <math>A(x_0+\Delta x)-A(x_0)=\int\limits_a^{x_0+\Delta x} f-\int\limits_a^{x_0} f=\int\limits_{x_0}^{x_0+\Delta x} f</math> ולכן <math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f</math>. נעיר ש-<math>\int\limits_{x_0}^{x_0+\Delta x} f(x_0)=f(x_0)\Delta x</math> (כי <math>f(x_0)</math> פונקציה קבועה). לכן <math>f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f(x_0)</math>. מכאן ש-<math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}\Big(f(t)-f(x_0)\Big)\mathrm dt</math>. נותר להוכיח שכאשר <math>\Delta x\to0</math> אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי <math>\varepsilon>0</math> נתון. כיוון ש-f רציפה ב-<math>x_0</math> קיים <math>\delta>0</math> כך שאם <math>|t-x_0|<\delta</math> אז <math>|f(t)-f(x_0)|<\varepsilon</math>. כעת נניח ש-<math>|\Delta x|<\delta</math>. אם כן האינטגרל באגף ימין הוא על קטע בין <math>x_0</math> ל-<math>x_0+\Delta x</math> ולכן כל t בקטע זה מקיים <math>|t-x_0|<\Delta x</math>. נובע שלכל t בקטע <math>|f(t)-f(x_0)|<\varepsilon</math>. יוצא שאם <math>|\Delta x|\le\delta</math> אז <math>\left|\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)\right|=\left|\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}(f(t)-f(x_0))\mathrm dt\right|<\ | + | # כיוון ש-f אינטגרבילית ב-<math>[a,b]</math> משפט 9 נותן שלכל <math>x\in[a,b]</math> f אינטגרבילית בקטע <math>[a,x_0]</math> ולכן <math>A(x)=\int\limits_a^x f</math> מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה: <math>|f(x)|\le M</math> לכל <math>x\in[a,b]</math>. כעת אם <math>x,y\in[a,b]</math> אז <math>|A(y)-A(x)|=\left|\int\limits_a^y f-\int\limits_a^x f\right|=\left|\int\limits_x^y f\right|\le M|y-x|</math> ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה <math>x_0\in[a,b]</math>. ר"ל A גזירה שם. ובכן <math>A(x_0+\Delta x)-A(x_0)=\int\limits_a^{x_0+\Delta x} f-\int\limits_a^{x_0} f=\int\limits_{x_0}^{x_0+\Delta x} f</math> ולכן <math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f</math>. נעיר ש-<math>\int\limits_{x_0}^{x_0+\Delta x} f(x_0)=f(x_0)\Delta x</math> (כי <math>f(x_0)</math> פונקציה קבועה). לכן <math>f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f(x_0)</math>. מכאן ש-<math>\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}\Big(f(t)-f(x_0)\Big)\mathrm dt</math>. נותר להוכיח שכאשר <math>\Delta x\to0</math> אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי <math>\varepsilon>0</math> נתון. כיוון ש-f רציפה ב-<math>x_0</math> קיים <math>\delta>0</math> כך שאם <math>|t-x_0|<\delta</math> אז <math>|f(t)-f(x_0)|<\varepsilon</math>. כעת נניח ש-<math>|\Delta x|<\delta</math>. אם כן האינטגרל באגף ימין הוא על קטע בין <math>x_0</math> ל-<math>x_0+\Delta x</math> ולכן כל t בקטע זה מקיים <math>|t-x_0|<\Delta x</math>. נובע שלכל t בקטע <math>|f(t)-f(x_0)|<\varepsilon</math>. יוצא שאם <math>|\Delta x|\le\delta</math> אז <math>\left|\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)\right|=\left|\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}(f(t)-f(x_0))\mathrm dt\right|<\frac{|\Delta x|\varepsilon}{|\Delta x|}</math>. הדבר נכון לכל <math>\varepsilon>0</math>, לכן <math>\lim_{\Delta x\to0}\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=0</math> ז"א <math>A'(x_0)</math> קיים ושווה ל-<math>f(x_0)</math>. {{משל}} |
# נתון ש-f רציפה בכל <math>[a,b]</math>. לפי החלק הקודם <math>\forall x\in[a,b]:\ A'(x)=f(x)</math>, כלומר A קדומה ל-f ב-<math>[a,b]</math>. קיים קבוע c כך ש-<math>F(x)=A(x)+c</math> לכל <math>x\in[a,b]</math>. מכאן ש-<math>F(b)-F(a)=A(b)+c-\Big(A(a)+c\Big)=A(b)-A(a)=\int\limits_a^b f-\int\limits_a^a f=\int\limits_a^b f</math>. {{משל}} | # נתון ש-f רציפה בכל <math>[a,b]</math>. לפי החלק הקודם <math>\forall x\in[a,b]:\ A'(x)=f(x)</math>, כלומר A קדומה ל-f ב-<math>[a,b]</math>. קיים קבוע c כך ש-<math>F(x)=A(x)+c</math> לכל <math>x\in[a,b]</math>. מכאן ש-<math>F(b)-F(a)=A(b)+c-\Big(A(a)+c\Big)=A(b)-A(a)=\int\limits_a^b f-\int\limits_a^a f=\int\limits_a^b f</math>. {{משל}} | ||
| שורה 16: | שורה 16: | ||
אם f רציפה בקטע <math>[a,b]</math> אז קיימת לה פונקצייה קדומה ב-<math>[a,b]</math>. | אם f רציפה בקטע <math>[a,b]</math> אז קיימת לה פונקצייה קדומה ב-<math>[a,b]</math>. | ||
====הוכחה==== | ====הוכחה==== | ||
| − | כיוון ש-f רציפה בקטע <math>[a,b]</math> כולו | + | כיוון ש-f רציפה בקטע <math>[a,b]</math> כולו <math>A(x)=\int\limits_a^x f</math> קדומה ל-f ב-<math>[a,b]</math>. |
====דוגמאות==== | ====דוגמאות==== | ||
* <math>f(x)=e^{x^2}</math>. זו פונקציה אלמנטרית ומוגדרת בכל <math>\mathbb R</math>, ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית. | * <math>f(x)=e^{x^2}</math>. זו פונקציה אלמנטרית ומוגדרת בכל <math>\mathbb R</math>, ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית. | ||
| שורה 31: | שורה 31: | ||
| − | + | '''הגדרה:''' עבור <math>f(x)\ge0</math> רציפה ב-<math>[a,b]</math> נגדיר את השטח שמתחת לגרף של f ע"י <math>\int\limits_a^b f</math>. לפי זה, אם <math>f(x)\le0</math> ב-<math>[a,b]</math> אז <math>\int\limits_a^b f</math> = מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף". אם f מחליפה סימן אז <math>\int\limits_a^b f</math> = השטח מעל ציר ה-x פחות השטח מתחת לציר ה-x ולכן <math>\int\limits_a^b |f|</math> = השטח בין הגרף לציר ה-x. | |
| − | + | ||
| − | '''הגדרה:''' עבור <math>f(x)\ge0</math> רציפה ב-<math>[a,b]</math> נגדיר את השטח שמתחת לגרף של f ע"י <math>\int\limits_a^b f</math>. לפי זה, אם <math>f(x)\le0</math> ב-<math>[a,b]</math> אז <math>\int\limits_a^b f</math> = מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף" | + | |
===דוגמת חישוב=== | ===דוגמת חישוב=== | ||
| − | + | [[קובץ:שטח בין גרפים.png|200px|ימין]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | בגרף שמשמאל ברור שהשטח בין הגרפים הוא <math>\int\limits_a^b f-g</math>, ובנימוק פשוט זה נכון בכל מקרה ש-<math>f(x)\ge g(x)</math> ב-<math>[a,b]</math>. | |
| − | |||
| + | למשל, נחשב את השטח שבין הגרפים <math>y=\sin(x)</math> ו-<math>y=\cos(x)</math> בקטע <math>\left[0,\tfrac\pi2\right]</math>: | ||
| + | <div align="center">[[קובץ:שטח בין סינוס לקוסינוס.png|400px]]</div> | ||
בקטע <math>\left[0,\tfrac\pi4\right]</math> מתקיים <math>\cos(x)\ge\sin(x)</math> ובקטע <math>\left[\tfrac\pi4,\tfrac\pi2\right]</math> מתקיים <math>\cos(x)\le\sin(x)</math>. לכן השטח הוא {{left|<math>\begin{align}\int\limits_0^\frac\pi2 |\cos(x)-\sin(x)|\mathrm dx&=\int\limits_0^\frac\pi4 \Big(\cos(x)-\sin(x)\Big)\mathrm dx+\int\limits_\frac\pi4^\frac\pi2 \Big(\sin(x)-\cos(x)\Big)\mathrm dx\\&=\left([\sin(x)+\cos(x)]_{x=0}^\frac\pi4\right)+\left([-\sin(x)-\cos(x)]_{x=\frac\pi4}^\frac\pi2\right)\\&=\left(\frac\sqrt22+\frac\sqrt22-(0+1)\right)+\left(-1-0+\frac\sqrt22+\frac\sqrt22\right)\\&=2\sqrt2-2\end{align}</math>}} | בקטע <math>\left[0,\tfrac\pi4\right]</math> מתקיים <math>\cos(x)\ge\sin(x)</math> ובקטע <math>\left[\tfrac\pi4,\tfrac\pi2\right]</math> מתקיים <math>\cos(x)\le\sin(x)</math>. לכן השטח הוא {{left|<math>\begin{align}\int\limits_0^\frac\pi2 |\cos(x)-\sin(x)|\mathrm dx&=\int\limits_0^\frac\pi4 \Big(\cos(x)-\sin(x)\Big)\mathrm dx+\int\limits_\frac\pi4^\frac\pi2 \Big(\sin(x)-\cos(x)\Big)\mathrm dx\\&=\left([\sin(x)+\cos(x)]_{x=0}^\frac\pi4\right)+\left([-\sin(x)-\cos(x)]_{x=\frac\pi4}^\frac\pi2\right)\\&=\left(\frac\sqrt22+\frac\sqrt22-(0+1)\right)+\left(-1-0+\frac\sqrt22+\frac\sqrt22\right)\\&=2\sqrt2-2\end{align}</math>}} | ||
{{משל}} | {{משל}} | ||
גרסה אחרונה מ־20:33, 29 ביולי 2012
את ההוכחה למשפט 11 לא סיימנו בשיעור הקודם ולכן השלמנו זאת ב־1.3.11. חלק זה מופיע בסיכום השיעור הקודם ולא בדף הנוכחי.
תוכן עניינים
האינטגרל לפי רימן (המשך)
משפט 12 (המשפט היסודי של חשבון אינטגרלי)
תהי f מוגדרת ואינטגרבילית בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
- לכל
![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) נגדיר
נגדיר 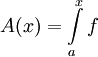 . אזי A מוגדרת היטב ורציפה ב-
. אזי A מוגדרת היטב ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ולכל
ולכל ![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) שבה f רציפה A גזירה כך ש-
שבה f רציפה A גזירה כך ש-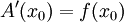 .
. - נוסחת ניוטון-לייבניץ: נניח ש-f רציפה בכל הקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אם F קדומה ל-f אז
. אם F קדומה ל-f אז ![\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)](/images/math/9/9/1/9910c3fea84d530a4ddc29cee79f0db3.png) .
.
הוכחה
- כיוון ש-f אינטגרבילית ב-
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) משפט 9 נותן שלכל
משפט 9 נותן שלכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) f אינטגרבילית בקטע
f אינטגרבילית בקטע ![[a,x_0]](/images/math/8/a/e/8aefd24e7c796fd419c690453435a4e6.png) ולכן
ולכן 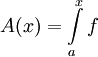 מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה:
מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה: 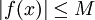 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . כעת אם
. כעת אם ![x,y\in[a,b]](/images/math/c/b/7/cb79e328f847e7458950b6147a06dbba.png) אז
אז 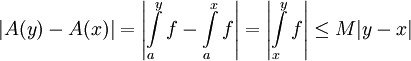 ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה
ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה ![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) . ר"ל A גזירה שם. ובכן
. ר"ל A גזירה שם. ובכן 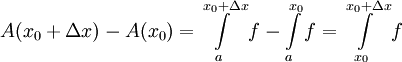 ולכן
ולכן 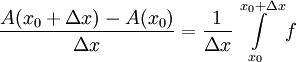 . נעיר ש-
. נעיר ש-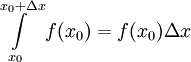 (כי
(כי 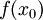 פונקציה קבועה). לכן
פונקציה קבועה). לכן 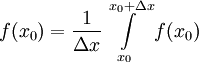 . מכאן ש-
. מכאן ש-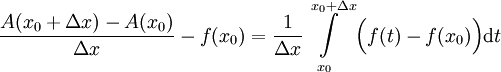 . נותר להוכיח שכאשר
. נותר להוכיח שכאשר 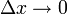 אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי
אגף ימין (ולכן אגף שמאל) שואף ל-0. לצורך זה יהי 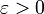 נתון. כיוון ש-f רציפה ב-
נתון. כיוון ש-f רציפה ב-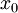 קיים
קיים 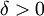 כך שאם
כך שאם  אז
אז 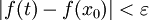 . כעת נניח ש-
. כעת נניח ש- . אם כן האינטגרל באגף ימין הוא על קטע בין
. אם כן האינטגרל באגף ימין הוא על קטע בין 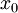 ל-
ל-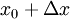 ולכן כל t בקטע זה מקיים
ולכן כל t בקטע זה מקיים 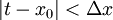 . נובע שלכל t בקטע
. נובע שלכל t בקטע 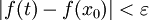 . יוצא שאם
. יוצא שאם 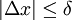 אז
אז  . הדבר נכון לכל
. הדבר נכון לכל 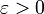 , לכן
, לכן 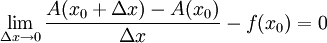 ז"א
ז"א 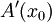 קיים ושווה ל-
קיים ושווה ל-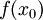 .
. 
- נתון ש-f רציפה בכל
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . לפי החלק הקודם
. לפי החלק הקודם ![\forall x\in[a,b]:\ A'(x)=f(x)](/images/math/b/3/e/b3eff8bb43fdeda0d0edfb6294af6278.png) , כלומר A קדומה ל-f ב-
, כלומר A קדומה ל-f ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . קיים קבוע c כך ש-
. קיים קבוע c כך ש-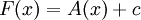 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . מכאן ש-
. מכאן ש-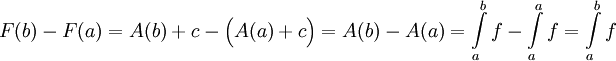 .
. 
מסקנה
אם f רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז קיימת לה פונקצייה קדומה ב-
אז קיימת לה פונקצייה קדומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
כיוון ש-f רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כולו
כולו 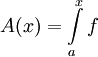 קדומה ל-f ב-
קדומה ל-f ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
דוגמאות
-
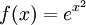 . זו פונקציה אלמנטרית ומוגדרת בכל
. זו פונקציה אלמנטרית ומוגדרת בכל  , ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית.
, ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית. -
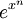 כאשר
כאשר 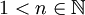
-
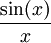
-
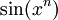
-
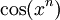
תרגילים לחידוד
- נגדיר
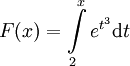 . נמצא את
. נמצא את 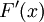 : לפי חלק א של משפט 12 מתקיים
: לפי חלק א של משפט 12 מתקיים 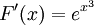 .
. 
- נגדיר
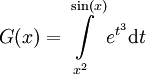 . נמצא את
. נמצא את 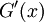 : נגדיר
: נגדיר 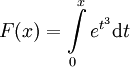 ולכן
ולכן 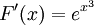 . לפי זה
. לפי זה 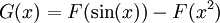 ולפיכך, ע"פ כלל השרשרת,
ולפיכך, ע"פ כלל השרשרת, 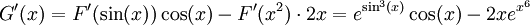 .
. 
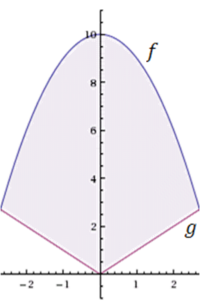
הגדרה: עבור 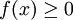 רציפה ב-
רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נגדיר את השטח שמתחת לגרף של f ע"י
נגדיר את השטח שמתחת לגרף של f ע"י 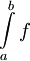 . לפי זה, אם
. לפי זה, אם 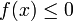 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 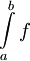 = מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף". אם f מחליפה סימן אז
= מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף". אם f מחליפה סימן אז 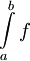 = השטח מעל ציר ה-x פחות השטח מתחת לציר ה-x ולכן
= השטח מעל ציר ה-x פחות השטח מתחת לציר ה-x ולכן 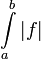 = השטח בין הגרף לציר ה-x.
= השטח בין הגרף לציר ה-x.
דוגמת חישוב
בגרף שמשמאל ברור שהשטח בין הגרפים הוא 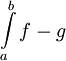 , ובנימוק פשוט זה נכון בכל מקרה ש-
, ובנימוק פשוט זה נכון בכל מקרה ש-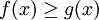 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
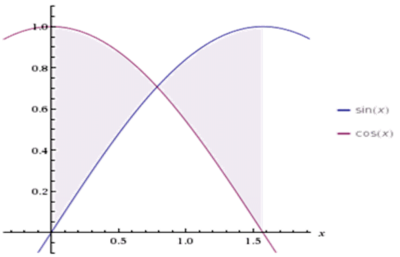
למשל, נחשב את השטח שבין הגרפים 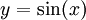 ו-
ו-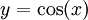 בקטע
בקטע ![\left[0,\tfrac\pi2\right]](/images/math/4/e/7/4e77a1302dd5d47f289db594d8f17338.png) :
:
![\left[0,\tfrac\pi4\right]](/images/math/a/d/4/ad443a23a524ee9b06986eb6c71924c7.png) מתקיים
מתקיים 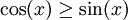 ובקטע
ובקטע ![\left[\tfrac\pi4,\tfrac\pi2\right]](/images/math/5/5/7/5570c0484decdccf0a3970f8cb0633d3.png) מתקיים
מתקיים 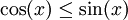 . לכן השטח הוא
. לכן השטח הוא ![\begin{align}\int\limits_0^\frac\pi2 |\cos(x)-\sin(x)|\mathrm dx&=\int\limits_0^\frac\pi4 \Big(\cos(x)-\sin(x)\Big)\mathrm dx+\int\limits_\frac\pi4^\frac\pi2 \Big(\sin(x)-\cos(x)\Big)\mathrm dx\\&=\left([\sin(x)+\cos(x)]_{x=0}^\frac\pi4\right)+\left([-\sin(x)-\cos(x)]_{x=\frac\pi4}^\frac\pi2\right)\\&=\left(\frac\sqrt22+\frac\sqrt22-(0+1)\right)+\left(-1-0+\frac\sqrt22+\frac\sqrt22\right)\\&=2\sqrt2-2\end{align}](/images/math/0/5/d/05d97e9286e66c19908e1846480de557.png)