משתמש:אור שחף/133 - הרצאה/24.5.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
תוכן עניינים
טורי חזקות (המשך)
משפט 2
יהי 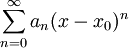 טור חזקות שרדיוס ההתכנסות שלו הוא R. אם קיים
טור חזקות שרדיוס ההתכנסות שלו הוא R. אם קיים 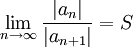 במובן הרחב אז
במובן הרחב אז 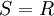 .
.
הוכחה
יהי x כרצוננו ונוכיח שאם 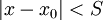 אז הטור מתכנס בהחלט, ואם
אז הטור מתכנס בהחלט, ואם 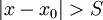 אז הוא מתבדר. נסמן את איברי הטור כ-
אז הוא מתבדר. נסמן את איברי הטור כ-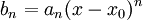 ולכן אם
ולכן אם 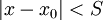 אזי
אזי  ואם
ואם 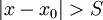 אזי
אזי 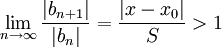 . ממבחן המנה של דאלמבר נסיק שהטור מתכנס בהחלט אם
. ממבחן המנה של דאלמבר נסיק שהטור מתכנס בהחלט אם 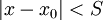 (ולכן
(ולכן 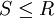 ) ואינו מתכנס בהחלט אם
) ואינו מתכנס בהחלט אם 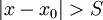 (ולכן
(ולכן 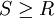 ). מכאן ש-
). מכאן ש-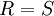 .
. 
דוגמאות
בתרגילים הבאים נמצא את רדיוס ההתכנסות R של הטור הנתון.
-
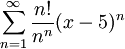 . אם קיים הגבול הבא אז הוא שווה לרדיוס ההתכנסות:
. אם קיים הגבול הבא אז הוא שווה לרדיוס ההתכנסות: 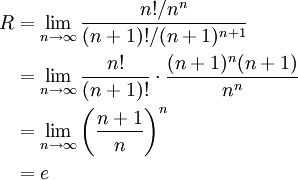

-
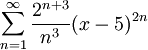 . דרך ראשונה: נעשה זאת לפי מבחן המנה:
. דרך ראשונה: נעשה זאת לפי מבחן המנה: 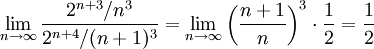 , אבל קיבלנו תוצאה שגויה - זה לא רדיוס ההתכנסות כי חישבנו
, אבל קיבלנו תוצאה שגויה - זה לא רדיוס ההתכנסות כי חישבנו 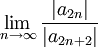 במקום
במקום 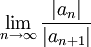 . עם זאת, נשים לב שאם נציב
. עם זאת, נשים לב שאם נציב 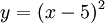 אז חישבנו את רדיוס ההתכנסות של
אז חישבנו את רדיוס ההתכנסות של 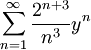 . מכאן שהטור מתכנס כאשר
. מכאן שהטור מתכנס כאשר 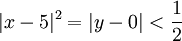 , כלומר כאשר
, כלומר כאשר 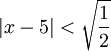 , ולכן הוא
, ולכן הוא 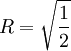 .
.  דרך שנייה: נחשב בעזרת מבחן השורש:
דרך שנייה: נחשב בעזרת מבחן השורש: ![R=1/\overline{\lim_{n\to\infty}}\sqrt[n]{a_n}](/images/math/7/e/a/7ea8e97f98b06d647fc2ea1392824f26.png) . גם כאן יש מכשול כי
. גם כאן יש מכשול כי 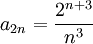 ואילו
ואילו 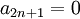 . לגבי האינדקסים האי-זוגיים
. לגבי האינדקסים האי-זוגיים ![\lim_{n\to\infty}\sqrt[2n+1]{a_{2n+1}}=0](/images/math/8/3/d/83dfc1d4cab8c60f923eb1b681ac3445.png) ולגבי הזוגיים
ולגבי הזוגיים ![\lim_{n\to\infty}\sqrt[2n]{a_{2n}}=\lim_{n\to\infty}\frac{\sqrt[2n]{2^{n+3}}}{\sqrt[2n]{n^3}}=\lim_{n\to\infty}\frac{2^{\frac12+\frac3{2n}}}{\left(\sqrt[n]{n}\right)^{3/2}}=\frac{2^\frac12}1=\sqrt2](/images/math/a/8/d/a8d4c731fe46aea2b536e9d21bf16b6b.png) . לכן
. לכן ![\limsup_{n\to\infty}\sqrt[n]{a_n}=\sqrt2](/images/math/3/f/8/3f81a10dc6af3adc18b80b9be659a4a8.png) ולפיכך
ולפיכך 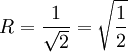 .
. 
-
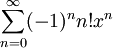 . לפי מבחן המנה:
. לפי מבחן המנה: 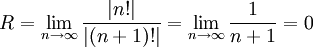 .
.  מכאן שהטור מתכנס רק עבור
מכאן שהטור מתכנס רק עבור 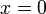 .
. - דוגמה כללית של טור חזקות ניתנת ע"י טור טיילור. נניח ש-f מוגדרת וגזירה
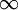 פעמים בסביבת
פעמים בסביבת 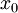 . לכל
. לכל 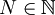 ניתן לכתוב
ניתן לכתוב 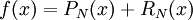 , ולכן
, ולכן 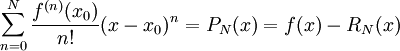 . אם עבור x מסויים
. אם עבור x מסויים 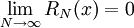 אזי
אזי 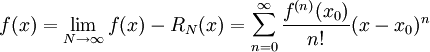 , וטור זה יקרא "טור טיילור של f סביב
, וטור זה יקרא "טור טיילור של f סביב 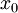 ". עבור
". עבור 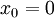 הטור יקרא "טור מקלורן של f", וכבר ראינו דוגמה לטור כזה:
הטור יקרא "טור מקלורן של f", וכבר ראינו דוגמה לטור כזה: 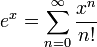 , שרדיוס ההתכנסות שלו הוא
, שרדיוס ההתכנסות שלו הוא 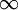 :
: 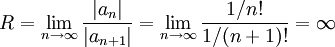 .
.
דוגמאות נוספות
- נקח
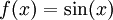 ו-
ו-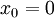 . נחשב טור טיילור (בפרט, טור מקלורן) ונקבל
. נחשב טור טיילור (בפרט, טור מקלורן) ונקבל 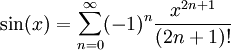 , בתנאי ש-
, בתנאי ש-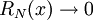 . נוכיח שזה אכן מתקיים:
. נוכיח שזה אכן מתקיים: 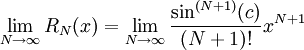 לכל
לכל 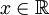 , כאשר c בין 0 ל-x. אבל ידוע ש-
, כאשר c בין 0 ל-x. אבל ידוע ש-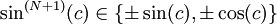 ולכן
ולכן 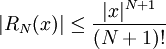 . עתה יהי
. עתה יהי 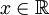 מסויים וניצור סדרה
מסויים וניצור סדרה 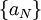 כך ש-
כך ש-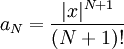 . נותר להוכיח ש-
. נותר להוכיח ש-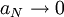 , ולכן מספיק להוכיח ש-
, ולכן מספיק להוכיח ש-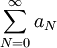 מתכנס. נעשה זאת באמצעות מבחן המנה של דאלמבר:
מתכנס. נעשה זאת באמצעות מבחן המנה של דאלמבר: 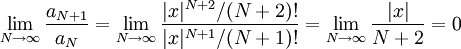 .
. 
- נגדיר
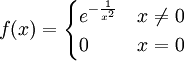 ונוכיח ש-f גזירה
ונוכיח ש-f גזירה 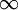 פעמים ב-
פעמים ב-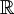 וש-
וש-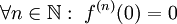 .
.
טענה 1: אם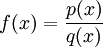 פונקציה רציונלית אזי
פונקציה רציונלית אזי 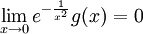 . הוכחה: קיים
. הוכחה: קיים 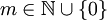 כך ש-
כך ש-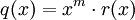 עבור פולינום r שמקיים
עבור פולינום r שמקיים 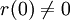 . לפיכך, עבור
. לפיכך, עבור 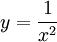 ,
, 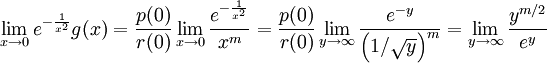 , ואחרי הפעלת כלל לופיטל
, ואחרי הפעלת כלל לופיטל 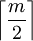 פעמים נקבל 0.
פעמים נקבל 0.
טענה 2: לכל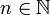 ולכל
ולכל 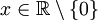 מתקיים
מתקיים 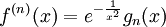 עבור פונקציה רציונלית
עבור פונקציה רציונלית 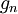 כלשהי כך ש-
כלשהי כך ש-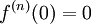 . הוכחה: נוכיח באינדוקציה. עבור
. הוכחה: נוכיח באינדוקציה. עבור 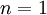 :
: 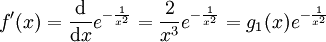 וכן
וכן 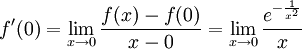 , ולפי טענה 1 זה שווה ל-0. עתה נוכיח עבור
, ולפי טענה 1 זה שווה ל-0. עתה נוכיח עבור 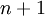 :
: 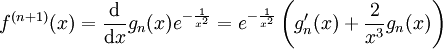 . כמו כן
. כמו כן 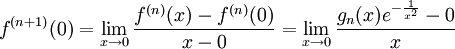 , ולפי טענה 1 זה שווה 0.
, ולפי טענה 1 זה שווה 0.  נובע מכך שטור מקלורן של f הוא
נובע מכך שטור מקלורן של f הוא 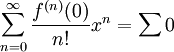 , שלא שווה ל-
, שלא שווה ל-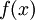 לכל x מלבד 0.
לכל x מלבד 0.
משפט 3
יהי טור חזקות 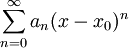 בעל רדיוס התכנסות
בעל רדיוס התכנסות  . אזי:
. אזי:
- בקטע
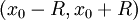 מוגדרת פונקציה גבולית רציפה
מוגדרת פונקציה גבולית רציפה 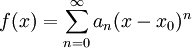 .
. - בקטע זה הפונקציה הגבולית גזירה ומתקיים
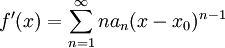 . לטור הגזור יש אותו רדיוס התכנסות R.
. לטור הגזור יש אותו רדיוס התכנסות R. - עבור
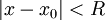 מתקיים
מתקיים 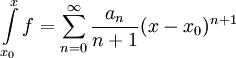 , וגם לטור הזה רדיוס התכנסות R.
, וגם לטור הזה רדיוס התכנסות R.
הוכחה
- יהי
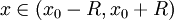 כרצונינו ונבחר r המקיים
כרצונינו ונבחר r המקיים 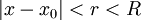 . לפי משפט 1, סעיף 3, הטור מתכנס במ"ש ב-
. לפי משפט 1, סעיף 3, הטור מתכנס במ"ש ב-![[x_0-r,x_0+r]](/images/math/a/1/d/a1d1994cd939c738504f99171ece9d05.png) . כמו כן, טור חזקות הוא סכום של פונקציות רציפות, ולכן f רציפה בקטע
. כמו כן, טור חזקות הוא סכום של פונקציות רציפות, ולכן f רציפה בקטע ![[x_0-r,x_0+r]](/images/math/a/1/d/a1d1994cd939c738504f99171ece9d05.png) ובפרט בנקודה x.
ובפרט בנקודה x. 
- הוכחנו בעבר כי ניתן לגזור טור איבר-איבר אם הוא מתכנס בנקודה אחת ואם הטור הגזור מתכנס במ"ש. התכנסות הטור נתונה בקטע
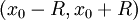 והטור הגזור הוא
והטור הגזור הוא 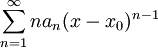 , לכן צריך רק להוכיח שהטור הגזור מתכנס במ"ש. תחילה נקבע את רדיוס ההתכנסות שלו: נסמן ב-S את רדיוס ההתכנסות של הטור הגזור ולכן
, לכן צריך רק להוכיח שהטור הגזור מתכנס במ"ש. תחילה נקבע את רדיוס ההתכנסות שלו: נסמן ב-S את רדיוס ההתכנסות של הטור הגזור ולכן ![\frac1S=\overline{\lim_{n\to\infty}}\sqrt[n]{n|a_n|}=\overline{\lim_{n\to\infty}}\sqrt[n]n\sqrt[n]{|a_n|}=\overline{\lim_{n\to\infty}}\sqrt[n]{|a_n|}=\frac1R](/images/math/3/0/7/307ea31a5060830947621ccba705144e.png) , כלומר
, כלומר 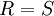 . נובע (לפי סעיף 1) שהטור הגזור מתכנס במ"ש ב-
. נובע (לפי סעיף 1) שהטור הגזור מתכנס במ"ש ב-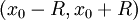 ולכן מתקיימים התנאים כדי להוכיח שהגזירה הנ"ל אכן היתה מוצדקת.
ולכן מתקיימים התנאים כדי להוכיח שהגזירה הנ"ל אכן היתה מוצדקת. 
את ההמשך עשינו בשיעור שאחריו:
- נבחר x מסויים בקטע
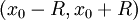 ונסמן
ונסמן 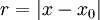 . עפ"י משפט 1, סעיף 3, ידוע שהטור שלנו מתכנס במ"ש בקטע בין
. עפ"י משפט 1, סעיף 3, ידוע שהטור שלנו מתכנס במ"ש בקטע בין 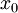 ל-x ולכן (לפי משפט 9 בפרק הקודם) מותר לבצע אינטגרציה איבר-איבר בקטע זה. כעת
ל-x ולכן (לפי משפט 9 בפרק הקודם) מותר לבצע אינטגרציה איבר-איבר בקטע זה. כעת 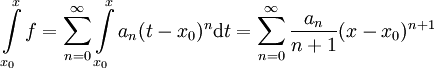 ולכן נותר למצוא רדיוס התכנסות. במילא נגזרת הטור החדש היא הטור המקורי, ולכן (מסעיף 2) יש להם אותו רדיוס התכנסות.
ולכן נותר למצוא רדיוס התכנסות. במילא נגזרת הטור החדש היא הטור המקורי, ולכן (מסעיף 2) יש להם אותו רדיוס התכנסות. 