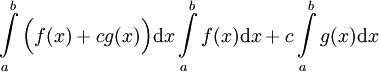משתמש:אור שחף/133 - הרצאה/27.2.11
...
הכללה: אם 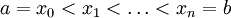 ואם f אינטגרבילית ב-
ואם f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 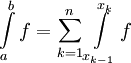 . הוכחה באינדוקציה.
. הוכחה באינדוקציה.
מוסכמות:
-
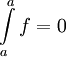
- אם
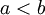 ואם f אינטגרבילית ב-
ואם f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נרשום
נרשום 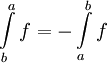
עם מוסכמות אלה יתקיים:
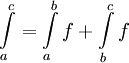 . באופן בלתי תלוי בסדר של המספרים a,b,c.
למשל: אם
. באופן בלתי תלוי בסדר של המספרים a,b,c.
למשל: אם 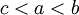 אז לפי משפט 8
אז לפי משפט 8 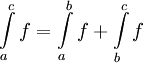 . נבדוק:
. נבדוק: 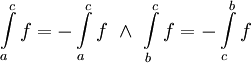 ולכן
ולכן  , מה שנכון כי
, מה שנכון כי 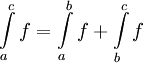 .
.
תוכן עניינים
משפט 9
תהי 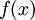 מוגדרת וחסומה ב-
מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . עוד נניח ש-f רציפה ב-
. עוד נניח ש-f רציפה ב-![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) . אזי f אינטגרבילית ב-
. אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
יהי 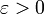 נתון. נגדיר
נתון. נגדיר 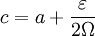 גרף (1). לפי הנתון f רציפה ב-
גרף (1). לפי הנתון f רציפה ב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) . לכן נוכל לבחור חלוקה P של
. לכן נוכל לבחור חלוקה P של ![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) כך ש-
כך ש-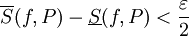 . כעת גדיר חלוקה Q של
. כעת גדיר חלוקה Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ע"י
ע"י 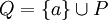 . עוד נגדיר
. עוד נגדיר 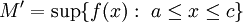 וכן
וכן 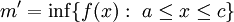 . נובע ש-
. נובע ש-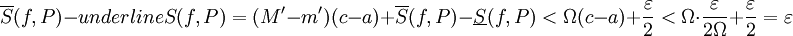 . נובע ממשפט 4 ש-f אינטגרבילית ב-
. נובע ממשפט 4 ש-f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. 
מסקנה 1
המשפט נכון אם f חסומה ורציפה ב-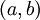 .
.
מסקנה 2
נניח ש-f חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ורציפה שם פרט למספר סופי של נקודות
ורציפה שם פרט למספר סופי של נקודות 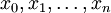 כך ש-
כך ש-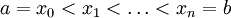 אזי f אינטגרבילית ב-
אזי f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
הוכחה
עבור כל k, f חסומה ב-![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) ורציפה ב-
ורציפה ב-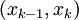 . לפי מסקנה 1 f אינטגרבילית ב-
. לפי מסקנה 1 f אינטגרבילית ב-![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) . נסתמך על מסקנה למשפט 8 לומר ש-f אינטגרבילית ב-
. נסתמך על מסקנה למשפט 8 לומר ש-f אינטגרבילית ב-![[a,b]=\bigcup_{k=1}^n [x_{k-1},x_k]](/images/math/8/0/d/80d3c82e91b924c56d753760172fe8d6.png) .
. 
הגדרה: אומרים ש-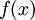 "רציפה למקוטעין" ב-
"רציפה למקוטעין" ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון.
גרף (2)
נובע ממסקנה 2 שכל פונקציה רציפה למקוטעין ב-
אם היא רציפה שם פרט למספר סופי של נקודות אי-רציפות ממין ראשון.
גרף (2)
נובע ממסקנה 2 שכל פונקציה רציפה למקוטעין ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אינטגרבילית שם. באופן דומה אפשר להוכיח שאם
אינטגרבילית שם. באופן דומה אפשר להוכיח שאם 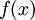 מוגדרת ומונוטונית למקוטעין ב-
מוגדרת ומונוטונית למקוטעין ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אך היא אינטגרבילית שם שם.
אך היא אינטגרבילית שם שם.
אינטגרביליות לפי רימן
נניח ש-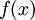 מוגדרת וחסומה ב-
מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נבחר חלוקה P של
. נבחר חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
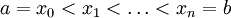 . עוד נבחר מספרים
. עוד נבחר מספרים ![c_k\in[x_{k-1},x_k]](/images/math/c/b/b/cbbb2a7a61cd7e98c21895f0cabd6417.png) ונכנה ב-P' את התת חלוקה
ונכנה ב-P' את התת חלוקה 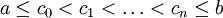 . ז"א
. ז"א 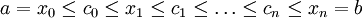 . בהתאם לכן נבנה סכום רימן
. בהתאם לכן נבנה סכום רימן 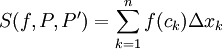 כאשר לכל k מתקיים
כאשר לכל k מתקיים 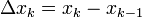 .
גרף (3)
.
גרף (3)
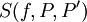 מקרב את השטח שמתחת לגרף, ולא ידוע אם הוא גדול, קטן או שווה לשטח שמתחת לגרף.
מקרב את השטח שמתחת לגרף, ולא ידוע אם הוא גדול, קטן או שווה לשטח שמתחת לגרף.
נעיר שעל חלוקה אחת P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אפשר לבנות אינסוף סכומי רימן
אפשר לבנות אינסוף סכומי רימן 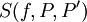 . עם זאת יתקיים תמיד
. עם זאת יתקיים תמיד 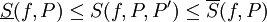 . יתר על כן,
. יתר על כן, 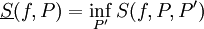 ו-
ו-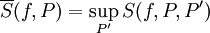 .
.
ההגדרת רימן: תהי 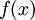 מוגדרת וחסומה ב-
מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נאמר ש-f אינטגרבילית ב-
. נאמר ש-f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם כאשר
אם כאשר 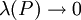 כל סכומי רימן
כל סכומי רימן 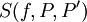 שואפים לגבול אחד, שיסומן
שואפים לגבול אחד, שיסומן 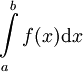 .
.
משפט 10
תהי f מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי f אינטגרבילית שם לפי רימן אם"ם f אינטגרבילית שם לפי דרבו, ואם כן אז
. אזי f אינטגרבילית שם לפי רימן אם"ם f אינטגרבילית שם לפי דרבו, ואם כן אז 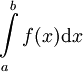 לפי רימן
לפי רימן 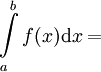 לפי דרבו.
לפי דרבו.
הוכחה
תחילה נניח ש-f אינטגרבילית לפי דרבו. נעיר שלכל חלוקה P ותת חלוקה P' של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
:
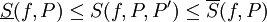 . כעת נשאיף
. כעת נשאיף  . כיוון ש-f אינטגרבילית דרבו,
. כיוון ש-f אינטגרבילית דרבו, 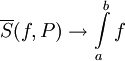 וכן
וכן 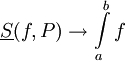 לכן משפט הסנדויץ' מבטיח ש-
לכן משפט הסנדויץ' מבטיח ש- קיים ושווה ל-
קיים ושווה ל-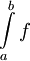 . ז"א f אינטגרבילית רימן ומתקיים
. ז"א f אינטגרבילית רימן ומתקיים 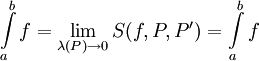 . לצד השני, נניח ש-f אינטגרבילית רימן. אזי מתקיים
. לצד השני, נניח ש-f אינטגרבילית רימן. אזי מתקיים 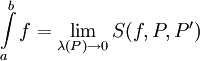 . אם כן הוא גם שווה ל-
. אם כן הוא גם שווה ל-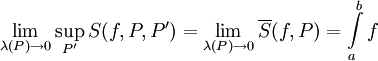 . מצאנו
. מצאנו 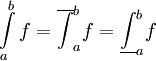 . עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם מצאנו:
. עצם זה שהאינטגרל העליון והתחתון שווים אומר ש-f אינטגרבילית דרבו וגם מצאנו: 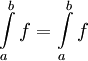 .
. 
באופן דומה נסיק 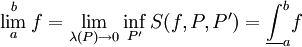
משפט 11
נניח ש-f ו-g מוגדרות ואינטגרביליות ב-[a,b], ונניח ש-c קבוע כלשהו. אזי:
-
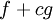 אינטגרבילית ב-[a,b] ומתקיים
אינטגרבילית ב-[a,b] ומתקיים 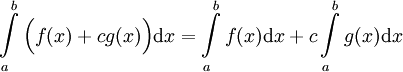
- אם
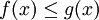 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) אז
אז 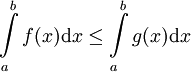 (מונוטוניות). בפרט אם
(מונוטוניות). בפרט אם ![\forall x\in[a,b]:\ f(x)\le0](/images/math/1/c/e/1ce0aaf03905bf5fb4bc0e2e94f00e32.png) אז
אז 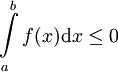 (חיוביות)
(חיוביות) -
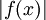 אינטגרבילית ומתקיים
אינטגרבילית ומתקיים 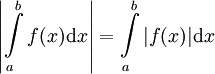 ואם
ואם 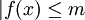 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 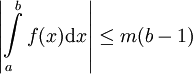
- אם
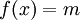 (פונקציה קבועה) אז
(פונקציה קבועה) אז 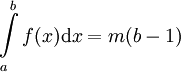
...
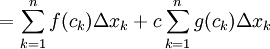 . נשאיף
. נשאיף 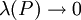 כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א
כיוון שנתון ש-f ו-g אינטגרביליות אגף ימין שואף לגבול, ז"א 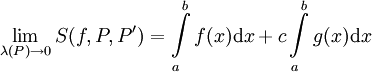 . עצם קיום הגבול אומר ש-
. עצם קיום הגבול אומר ש-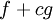 אינטגרבילית ולפי ערך הגבול נסיק
אינטגרבילית ולפי ערך הגבול נסיק