הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/20.2.11"
| (7 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | + | {{כותרת נושא|אינטגרביליות|נושא ראשון}} | |
'''מטרה:''' לחשב שטח (דו-מימדי במקרה שלנו, כי אינפי מדבר על <math>\mathbb R</math>). | '''מטרה:''' לחשב שטח (דו-מימדי במקרה שלנו, כי אינפי מדבר על <math>\mathbb R</math>). | ||
| − | (1) | + | גרף (1) |
נציג שתי שיטות עיקריות לחישוב שטחים: | נציג שתי שיטות עיקריות לחישוב שטחים: | ||
| שורה 9: | שורה 9: | ||
# אינטגרבליות לפי רימן | # אינטגרבליות לפי רימן | ||
| − | היום נדבר על | + | היום נדבר על הראשונה. |
| − | + | =אינטגרבליות לפי דרבו= | |
| − | + | נסמן <math>M_i:=\sup_{x\in[x_{i-1},x_i]} f(x)</math> ו-<math>m_i:=\inf_{x\in[x_{i-1},x_i]} f(x)</math>. לכל חלוקה T נגדיר <math>\overline S(T):=\sum_{i=1}^n M_i \Delta x_i</math> ו-<math>\underline S(T):=\sum_{i=1}^n m_i \Delta x_i</math>. | |
| + | כמו כן נגדיר | ||
| + | {{left| | ||
| + | <math>\overline I:=\inf\{\overline S(T):\ </math> חלוקה <math>T\}</math> | ||
| − | <math>\ | + | <math>\underline I:=\sup\{\underline S(T):\ </math> חלוקה <math>T\}</math> |
| + | }} | ||
| + | אם <math>\overline I=\underline I</math> אז f אינטגרבילית לפי דרבו וערך האינטגרל הוא ערך זה. | ||
| − | <math> | + | ==דוגמה 1== |
| + | הוכח עפ"י הגדרת האינטגרל שהפונקציה <math>f(x)=x</math> אינטגרבילית בקטע <math>[0,1]</math> ומצא עפ"י ההגדרה את ערך האינטגרל. | ||
| − | + | ===פתרון=== | |
| + | '''דרך 1:''' חישוב ע"י משולש. | ||
| − | ''' | + | '''דרך 2:''' נבחר חלוקה מספיק קטנה השואפת ל-0 (דרוש כי רוצים שסכום דרבו העליון יהא שווה לסכום דרבו התחתון). לדוגמה <math>\Delta x=\frac1n</math>. |
| − | + | במקרה זה נחלק את הקטע לפי הנקודות <math>0,\tfrac1n,\tfrac2n,\dots,\tfrac{n-1}n,1</math>, ז"א <math>\overline I=\lim_{n\to\infty} \underbrace{\frac1n}_{(1)}\underbrace{\sum_{i=1}^n \frac i n}_{(2)}</math>. | |
| + | # רוחב המלבן | ||
| + | # אורך המלבן | ||
| + | (נשים לב כי <math>f(x)=x</math> פונקציה עולה ולכן, בגלל שלקחנו נקודת קצה ימנית, קיבלנו סכום עליון) | ||
| − | + | באופן דומה נמצא סכום דרבו תחתון (עם נקודות קצה שמאליות): | |
| + | {{left| | ||
| + | <math>\underline I=\lim_{n\to\infty} \frac1n \sum_{i=0}^{n-1} \frac i n</math> | ||
| + | }} | ||
| + | אם נראה כי <math>\overline I=\underline I</math> נקבל כי f אינטגרבילית לפי דרבו (ואפילו נקבל את השטח). | ||
| − | + | נחשב: | |
| + | {{left| | ||
| + | <math>\overline I=\lim_{n\to\infty}\frac1{n^2}\sum_{i=1}^n i=\lim_{n\to\infty} \frac1{n^2}\cdot\frac{n(n+1)}2=\frac12</math> | ||
| − | + | <math>\underline I=\lim_{n\to\infty}\frac1{n^2}\sum_{i=0}^{n-1} i=\lim_{n\to\infty} \frac1{n^2}\cdot\frac{(n-1)n}{2}=\frac12</math> | |
| − | + | }} | |
| − | + | ||
| + | לכן f אינטגרבילית לפי דרבו והשטח מתחת לגרף הוא <math>\tfrac12</math>. {{משל}} | ||
| − | + | '''הערה:''' נשים לב שכדי להוכיח אינטגרביליות היינו יכולים להראות שלכל חלוקה כך ש-<math>\Delta x\to0</math> מתקיים <math>\overline I=\underline I</math>. | |
| − | + | ==דוגמה 2== | |
| + | חשב את השטח שמתחת לעקומה <math>y=9-x^2</math> בקטע <math>[0,3]</math>. קבע בפרוט אם f אינטגרבילית. | ||
| − | <math>\underline | + | ===פתרון=== |
| + | באופן כללי צריך לבחור חלוקה <math>T_n</math> שעבורה <math>\lambda(T_n)\to0</math>, למשל <math>x_i=\frac{3i}n</math> כאשר <math>n\to\infty</math> (ולכן <math>\Delta x_i=\frac3n\to0</math>). נבנה סכום דרבו מתאים: | ||
| + | {| | ||
| + | {{=|l=\underline S | ||
| + | |r=\lim_{n\to\infty}\sum_{i=0}^n\frac3n f\left(\frac{3i}n\right) | ||
| + | |c=ברור ש-<math>m_i=\inf_{x\in[x_{i-1},x_i]} f(x)=9-x_i^2</math> ולכן: | ||
| + | }} | ||
| + | {{=|r=\lim_{n\to\infty}\frac3n\sum_{i=0}^n\left(9-\frac{3^2i^2}{n^2}\right) | ||
| + | }} | ||
| + | {{=|r=\lim_{n\to\infty}\frac3n\cdot9n-\frac3n\cdot\frac9{n^2}\sum_{i=0}^n i^2 | ||
| + | }} | ||
| + | {{=|r=\lim_{n\to\infty}27-\frac{27}{n^3}\sum_{i=0}^n i^2 | ||
| + | }} | ||
| + | {{=|r=\lim_{n\to\infty}27-\frac{27}{n^3}\frac{n(n+1)(2n+1)}6 | ||
| + | }} | ||
| + | {{=|r=27-\frac{27\cdot2}6 | ||
| + | }} | ||
| + | {{=|r=18 | ||
| + | }} | ||
| + | |} | ||
| − | . | + | באותו אופן מגיעים ל-<math>\overline S=18</math> ולכן <math>\int\limits_0^3 f=18</math>. {{משל}} |
| − | אם נראה כי <math>\ | + | ==דוגמה 3== |
| + | הוכח או הפרך: אם {{ltr|{{!}}f{{!}}}} אינטגרבילית ב-<math>[a,b]</math> אז f אינטגרבילית ב-<math>[a,b]</math>. | ||
| + | |||
| + | ===פתרון=== | ||
| + | '''הפרכה:''' נבחר את הפונקציה <math>f(x)=\begin{cases}1&x\in\mathbb Q\\-1&x\not\in\mathbb Q\end{cases}=2D(x)-1</math> (כאשר <math>D(x)</math> היא פונקצית דיריכלה). ברור כי <math>|f|</math> אינטגרבילית (כי היא קבועה). לעומת זאת, אם נבחר חלוקה של מספרים אי רציונלים נחלק סכום שלילי, ואם נבחר חלוקה של מספרים רציונלים נקבל סכום חיובי. לכן f אינה אינטגרבילית. {{משל}} | ||
| + | |||
| + | '''הערה:''' זוהי דוגמה טובה שמראה שיש להוכיח שלכל חלוקה <math>\Delta x\to0</math>. | ||
| + | |||
| + | '''הערה:''' נראה בהמשך כי אינטגרביליות לפי רימן שקולה לאינטגרביליות לפי דרבו (שם אפשרי לבחור כל נקודה בתת קטע). הפתרון במקרה זה היה יכול להיות יפה יותר. | ||
| + | |||
| + | ==דוגמה 4== | ||
| + | הוכח או הפרך: אם f חסומה ב-<math>[a,b]</math> ולכל <math>[c,b]\subset[a,b]</math> f אינטגרבילית ב-<math>[c,b]</math> אז f אינטגרבילית ב-<math>[a,b]</math>. | ||
| + | |||
| + | ===פתרון=== | ||
| + | '''הוכחה:''' יהי <math>\varepsilon>0</math> נתון. המטרה שלנו היא להראות כי יש חלוקה <math>T_\varepsilon</math> של <math>[a,b]</math> המקיימת ש-<math>\overline S(T_\varepsilon)-\underline S(T_\varepsilon)<\varepsilon</math>. | ||
| + | |||
| + | נתון כי f אינטגרבילית ב-<math>[c,b]</math> ולכן יש חלוקה <math>T_{\varepsilon'}</math> של <math>[c,b]</math> עבורה מתקיים <math>\overline S(T_{\varepsilon'})-\underline S(T_{\varepsilon'})<\frac\varepsilon2</math>. נגדיר <math>T_\varepsilon:=T_{\varepsilon'}\cup\{a\}</math>. | ||
| − | + | נבנה סכום דרבו עליון ותחתון: | |
| − | <math>\overline | + | {{left| |
| + | <math>\overline S(T_\varepsilon)=\sup_{x\in[a,c]} f(x)\cdot (c-a)+\overline S(T_{\varepsilon'})</math> | ||
| − | + | <math>\underline S(T_\varepsilon)=\inf_{x\in[a,c]} f(x)\cdot (c-a)+\underline S(T_{\varepsilon'})</math> | |
| + | }} | ||
| + | לכן: | ||
| + | {| | ||
| + | {{=|l=\overline S(T_\varepsilon)-\underline S(T_\varepsilon) | ||
| + | |r=M(c-a)+\overline S(T_{\varepsilon'})-\underline S(T_{\varepsilon'})-m(c-a) | ||
| + | |c=נסמן <math>M:=\sup_{x\in[a,c]} f(x)</math> וכן <math>m:=\inf_{x\in[a,c]}f(x)</math>, לפיכך: | ||
| + | }} | ||
| + | {{=|r=(M-m)(c-a)+\overline S(T_{\varepsilon'})-\underline S(T_{\varepsilon'}) | ||
| + | }} | ||
| + | {{=|r=\frac\varepsilon2+\frac\varepsilon2 | ||
| + | |o=\le | ||
| + | |c=נבחר c כך ש- <math>(c-a)(M-m)=\frac\varepsilon{2}</math> (קיים כי כאשר <math>a<c\to a</math> מתקיים <math>M-m\to0</math> ולכן <math>(c-a)(M-m)\to0</math>) | ||
| + | }} | ||
| + | {{=|r=\varepsilon | ||
| + | }} | ||
| + | |} | ||
| + | {{משל}} | ||
| − | + | ==דוגמה 5== | |
| − | + | חשב <math>\lim_{n\to\infty}\frac1n\left(e^{\frac1n}+e^{\frac2n}+\dots+e^{\frac{n-1}n}+e\right)</math>. | |
| − | + | ===פתרון=== | |
| + | נשים לב שמוגדר למעשה סכום של מלבנים. נסתכל על הפונקציה <math>e^x</math> בקטע <math>[0,1]</math>. <math>e^x</math> פונקציה אינטגרבילית. הגבול הנתון הוא <math>\lim_{n\to\infty}\frac1n\sum_{i=1}^n e^{\frac{i}{n}}</math>, וזוהי בדיוק ההגדרה של אינטגרל מסויים. לכן <math>\lim_{n\to\infty}\frac1n\sum_{i=1}^n e^{\frac{i}{n}}=\int\limits_0^1 e^xdx</math>. | ||
| − | + | לפי המשפט היסודי זה שווה ל-<math>[e^x]_0^1=e^1-e^0=e-1</math> (הפונקציה הקדומה של <math>e^x</math> היא <math>e^x</math>). {{משל}} | |
| − | + | ---- | |
| − | + | '''משפט:''' תנאי הכרחי כדי שפונקציה <math>f(x)</math> תהיה אינטגרבילית ב-<math>[a,b]</math> הוא ש-f חסומה בקטע. | |
| − | + | '''משפט:''' אם f חסומה בקטע <math>[a,b]</math> ורציפה פרט אולי למספר סופי של נקודות אי רציפות אז f אינטגרבילית ב-<math>[a,b]</math>. | |
| − | <math> | + | ==דוגמה 6== |
| + | קבע מי מהפונקציות הבאות אינטגרבילית: | ||
| + | <ol> | ||
| + | <li> | ||
| + | <math>f(x)=\begin{cases}\tan(x)&0\le x<\tfrac\pi2\\1&x=\tfrac\pi2\end{cases}</math> בקטע <math>\left[0,\tfrac\pi2\right]</math>. | ||
| + | ===פתרון=== | ||
| + | '''לא אינטגרבילית:''' מתקיים <math>\lim_{k\to\frac\pi2^-}f(x)=\lim_{k\to\frac\pi2^-}\tan(x)=\lim_{k\to\frac\pi2^-}\frac{\sin(x)}{\cos(x)}=\infty</math>. לפיכך f לא חסומה ולכן לא אינטגרבילית. {{משל}} | ||
| + | </li> | ||
| + | <li> | ||
| + | <math>f(x)=\begin{cases}\sin\left(\frac1x\right)&x\ne0\\0&x=0\end{cases}</math> בקטע <math>[-1,1]</math>. | ||
| + | ===פתרון=== | ||
| + | '''כן אינטגרבילית:''' נשים לב כי <math>-1\le\sin\left(\frac1x\right)\le1</math>. בנוסף יש לנו נקודת אי-רציפות יחידה ב-<math>x=0</math> ולכן f אינטגרבילית. {{משל}} | ||
| + | </li> | ||
| + | </ol> | ||
גרסה אחרונה מ־16:18, 2 במרץ 2011
נושא ראשון:
אינטגרביליות
מטרה: לחשב שטח (דו-מימדי במקרה שלנו, כי אינפי מדבר על 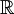 ).
).
גרף (1)
נציג שתי שיטות עיקריות לחישוב שטחים:
- אינטגרבליות לפי דרבו
- אינטגרבליות לפי רימן
היום נדבר על הראשונה.
תוכן עניינים
אינטגרבליות לפי דרבו
נסמן ![M_i:=\sup_{x\in[x_{i-1},x_i]} f(x)](/images/math/b/0/1/b01f316770b0e9e5117cc832418433d0.png) ו-
ו-![m_i:=\inf_{x\in[x_{i-1},x_i]} f(x)](/images/math/c/0/3/c0318a6e80caffd30743b445f5aaa0c7.png) . לכל חלוקה T נגדיר
. לכל חלוקה T נגדיר 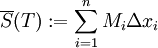 ו-
ו-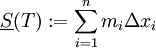 .
.
כמו כן נגדיר
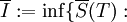 חלוקה
חלוקה 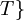
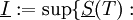 חלוקה
חלוקה 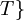
אם 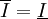 אז f אינטגרבילית לפי דרבו וערך האינטגרל הוא ערך זה.
אז f אינטגרבילית לפי דרבו וערך האינטגרל הוא ערך זה.
דוגמה 1
הוכח עפ"י הגדרת האינטגרל שהפונקציה 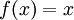 אינטגרבילית בקטע
אינטגרבילית בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) ומצא עפ"י ההגדרה את ערך האינטגרל.
ומצא עפ"י ההגדרה את ערך האינטגרל.
פתרון
דרך 1: חישוב ע"י משולש.
דרך 2: נבחר חלוקה מספיק קטנה השואפת ל-0 (דרוש כי רוצים שסכום דרבו העליון יהא שווה לסכום דרבו התחתון). לדוגמה 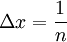 .
.
במקרה זה נחלק את הקטע לפי הנקודות 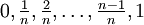 , ז"א
, ז"א 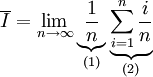 .
.
- רוחב המלבן
- אורך המלבן
(נשים לב כי 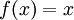 פונקציה עולה ולכן, בגלל שלקחנו נקודת קצה ימנית, קיבלנו סכום עליון)
פונקציה עולה ולכן, בגלל שלקחנו נקודת קצה ימנית, קיבלנו סכום עליון)
באופן דומה נמצא סכום דרבו תחתון (עם נקודות קצה שמאליות):
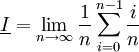
אם נראה כי 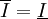 נקבל כי f אינטגרבילית לפי דרבו (ואפילו נקבל את השטח).
נקבל כי f אינטגרבילית לפי דרבו (ואפילו נקבל את השטח).
נחשב:

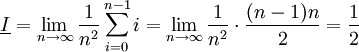
לכן f אינטגרבילית לפי דרבו והשטח מתחת לגרף הוא 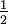 .
. 
הערה: נשים לב שכדי להוכיח אינטגרביליות היינו יכולים להראות שלכל חלוקה כך ש-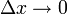 מתקיים
מתקיים 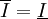 .
.
דוגמה 2
חשב את השטח שמתחת לעקומה 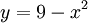 בקטע
בקטע ![[0,3]](/images/math/e/d/9/ed9c05fe24c0f49f5d73f494a921e0c4.png) . קבע בפרוט אם f אינטגרבילית.
. קבע בפרוט אם f אינטגרבילית.
פתרון
באופן כללי צריך לבחור חלוקה 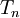 שעבורה
שעבורה 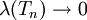 , למשל
, למשל 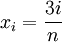 כאשר
כאשר 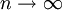 (ולכן
(ולכן 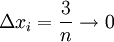 ). נבנה סכום דרבו מתאים:
). נבנה סכום דרבו מתאים:
ברור ש-![m_i=\inf_{x\in[x_{i-1},x_i]} f(x)=9-x_i^2](/images/math/d/d/7/dd74a76c6c978b983401bb01fd723830.png) ולכן: ולכן:
|
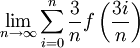
|

|
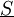
|
|||
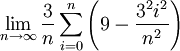
|

|
|||||
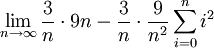
|

|
|||||
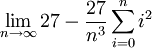
|

|
|||||
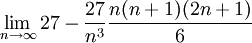
|

|
|||||
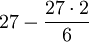
|

|
|||||
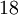
|

|
באותו אופן מגיעים ל-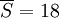 ולכן
ולכן 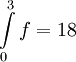 .
. 
דוגמה 3
הוכח או הפרך: אם |f| אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז f אינטגרבילית ב-
אז f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
פתרון
הפרכה: נבחר את הפונקציה 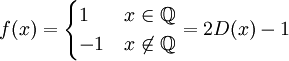 (כאשר
(כאשר 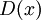 היא פונקצית דיריכלה). ברור כי
היא פונקצית דיריכלה). ברור כי 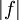 אינטגרבילית (כי היא קבועה). לעומת זאת, אם נבחר חלוקה של מספרים אי רציונלים נחלק סכום שלילי, ואם נבחר חלוקה של מספרים רציונלים נקבל סכום חיובי. לכן f אינה אינטגרבילית.
אינטגרבילית (כי היא קבועה). לעומת זאת, אם נבחר חלוקה של מספרים אי רציונלים נחלק סכום שלילי, ואם נבחר חלוקה של מספרים רציונלים נקבל סכום חיובי. לכן f אינה אינטגרבילית. 
הערה: זוהי דוגמה טובה שמראה שיש להוכיח שלכל חלוקה 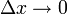 .
.
הערה: נראה בהמשך כי אינטגרביליות לפי רימן שקולה לאינטגרביליות לפי דרבו (שם אפשרי לבחור כל נקודה בתת קטע). הפתרון במקרה זה היה יכול להיות יפה יותר.
דוגמה 4
הוכח או הפרך: אם f חסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ולכל
ולכל ![[c,b]\subset[a,b]](/images/math/4/b/4/4b421a2c24ed570719689fcd0ec26b61.png) f אינטגרבילית ב-
f אינטגרבילית ב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) אז f אינטגרבילית ב-
אז f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
פתרון
הוכחה: יהי 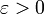 נתון. המטרה שלנו היא להראות כי יש חלוקה
נתון. המטרה שלנו היא להראות כי יש חלוקה 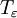 של
של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) המקיימת ש-
המקיימת ש-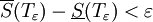 .
.
נתון כי f אינטגרבילית ב-![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) ולכן יש חלוקה
ולכן יש חלוקה 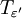 של
של ![[c,b]](/images/math/d/6/0/d6033df87877013a91e322ce6a5bc181.png) עבורה מתקיים
עבורה מתקיים 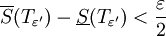 . נגדיר
. נגדיר 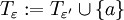 .
.
נבנה סכום דרבו עליון ותחתון:
![\overline S(T_\varepsilon)=\sup_{x\in[a,c]} f(x)\cdot (c-a)+\overline S(T_{\varepsilon'})](/images/math/a/d/f/adf98da2b0a39b0497dba9d5d6ec7f74.png)
![\underline S(T_\varepsilon)=\inf_{x\in[a,c]} f(x)\cdot (c-a)+\underline S(T_{\varepsilon'})](/images/math/e/4/4/e441d203a3f6fa252d0bea46ac185a92.png)
לכן:
נסמן ![M:=\sup_{x\in[a,c]} f(x)](/images/math/5/2/7/5278d9c16ddc4a16b0baab84807e9800.png) וכן וכן ![m:=\inf_{x\in[a,c]}f(x)](/images/math/9/f/6/9f6c5126ed1fc42e858b69e18b7d1474.png) , לפיכך: , לפיכך:
|
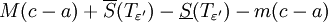
|

|
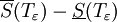
|
|||
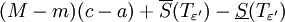
|

|
|||||
נבחר c כך ש- 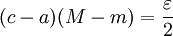 (קיים כי כאשר (קיים כי כאשר 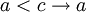 מתקיים מתקיים 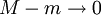 ולכן ולכן  ) )
|
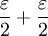
|
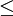
|
||||

|

|

דוגמה 5
חשב 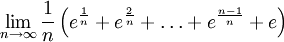 .
.
פתרון
נשים לב שמוגדר למעשה סכום של מלבנים. נסתכל על הפונקציה 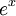 בקטע
בקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
. 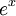 פונקציה אינטגרבילית. הגבול הנתון הוא
פונקציה אינטגרבילית. הגבול הנתון הוא 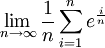 , וזוהי בדיוק ההגדרה של אינטגרל מסויים. לכן
, וזוהי בדיוק ההגדרה של אינטגרל מסויים. לכן 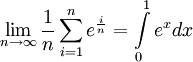 .
.
לפי המשפט היסודי זה שווה ל-![[e^x]_0^1=e^1-e^0=e-1](/images/math/d/9/3/d93c1d3af1c7b6047b0e23b4cd14bce5.png) (הפונקציה הקדומה של
(הפונקציה הקדומה של 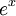 היא
היא 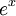 ).
). 
משפט: תנאי הכרחי כדי שפונקציה 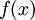 תהיה אינטגרבילית ב-
תהיה אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) הוא ש-f חסומה בקטע.
הוא ש-f חסומה בקטע.
משפט: אם f חסומה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ורציפה פרט אולי למספר סופי של נקודות אי רציפות אז f אינטגרבילית ב-
ורציפה פרט אולי למספר סופי של נקודות אי רציפות אז f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
דוגמה 6
קבע מי מהפונקציות הבאות אינטגרבילית:
-
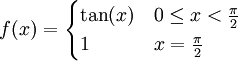 בקטע
בקטע ![\left[0,\tfrac\pi2\right]](/images/math/4/e/7/4e77a1302dd5d47f289db594d8f17338.png) .
.
פתרון
לא אינטגרבילית: מתקיים
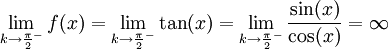 . לפיכך f לא חסומה ולכן לא אינטגרבילית.
. לפיכך f לא חסומה ולכן לא אינטגרבילית. 
-
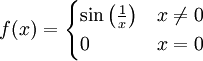 בקטע
בקטע ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) .
.
פתרון
כן אינטגרבילית: נשים לב כי
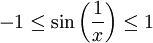 . בנוסף יש לנו נקודת אי-רציפות יחידה ב-
. בנוסף יש לנו נקודת אי-רציפות יחידה ב-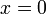 ולכן f אינטגרבילית.
ולכן f אינטגרבילית. 