הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' בר אילן, תשנ"א, מועד ב, שאלה 4"
מתוך Math-Wiki
מ |
מ |
||
| שורה 14: | שורה 14: | ||
| − | + | זהו גם הפ"מ של A: | |
| − | + | הפ"מ מחלק את הפ"א, לכן הפ"מ חייב להיות מהצורה <math>(x-1)^\alpha </math>, כאשר <math>\alpha \leq 3 \wedge \alpha \in\mathbb{N}</math>. | |
קל לבדוק ישירות שA-I בריבוע שונה ממטריצת אפסים בעוד בשלישית שווה למטריצת האפס. | קל לבדוק ישירות שA-I בריבוע שונה ממטריצת אפסים בעוד בשלישית שווה למטריצת האפס. | ||
גרסה מ־20:03, 26 בדצמבר 2011
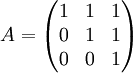
נמצא פ"א: 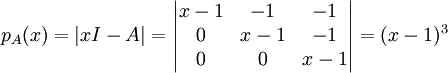 כי דטר' של מטר' משולשית היא מכפלת איברי האלכסון.
כי דטר' של מטר' משולשית היא מכפלת איברי האלכסון.
זהו גם הפ"מ של A:
הפ"מ מחלק את הפ"א, לכן הפ"מ חייב להיות מהצורה 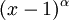 , כאשר
, כאשר 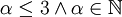 .
.
קל לבדוק ישירות שA-I בריבוע שונה ממטריצת אפסים בעוד בשלישית שווה למטריצת האפס.
קיבלנו שהמטריצה 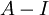 נילפ' מאינדקס 3, ולכן לפי משפט שהוכחנו הבלוק הגדול ביותר בצורת ז'ורדן שדומה לה הוא מסדר 3=אינדקס הנילפוטנטיות.
אבל המטר' היא כבר מסדר 3, ולכן בלוק זה חייב להיות הבלוק היחיד במטריצה. קיבלנו ש
נילפ' מאינדקס 3, ולכן לפי משפט שהוכחנו הבלוק הגדול ביותר בצורת ז'ורדן שדומה לה הוא מסדר 3=אינדקס הנילפוטנטיות.
אבל המטר' היא כבר מסדר 3, ולכן בלוק זה חייב להיות הבלוק היחיד במטריצה. קיבלנו ש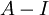 דומה לבלוק ז'ורדן נילפוטנטי מסדר 3.
דומה לבלוק ז'ורדן נילפוטנטי מסדר 3.
לפי הגדרת דמיון המטריצות, קיימת מטר' הפיכה 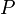 כך ש:
כך ש:
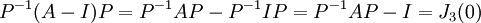
נעביר אגפים ונקבל: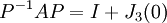
קיבלנו שצורת ז'ורדן הדומה ל-A היא 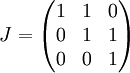
כנדרש! :)