הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' בר אילן, תשנ"א, מועד ב, שאלה 4"
| (5 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[תחרות חנוכה לינארית 2 תשעב|חזרה]] | ||
| + | |||
<math>A=\begin{pmatrix} | <math>A=\begin{pmatrix} | ||
1 & 1 & 1\\ | 1 & 1 & 1\\ | ||
| שורה 5: | שורה 7: | ||
\end{pmatrix} | \end{pmatrix} | ||
</math> | </math> | ||
| + | |||
| + | נסמן את סדר המטריצה <math>A</math> ב- <math>n</math>. | ||
נמצא פ"א: <math>p_A(x)=|xI-A|=\begin{vmatrix} | נמצא פ"א: <math>p_A(x)=|xI-A|=\begin{vmatrix} | ||
| שורה 16: | שורה 20: | ||
נראה שזהו גם הפ"מ של A: | נראה שזהו גם הפ"מ של A: | ||
| − | הפ"מ מחלק את הפ"א, והחזקה הn-ית (כאן 3) | + | הפ"מ מחלק את הפ"א, והחזקה הn-ית (כאן 3) של הפ"מ מתחלקת בפ״א. לכן הפ"מ חייב להיות מהצורה <math>(x-1)^\alpha </math>, כאשר <math>\alpha \leq 3 \wedge \alpha \in\mathbb{N}</math>. |
| + | |||
| + | ברור <math>(A-I)^1 \neq 0</math> | ||
| + | . | ||
נבדוק ישירות שA-I בריבוע שונה ממטריצת אפסים: <math>(A-I)^2=\begin{pmatrix} | נבדוק ישירות שA-I בריבוע שונה ממטריצת אפסים: <math>(A-I)^2=\begin{pmatrix} | ||
| שורה 40: | שורה 47: | ||
</math> | </math> | ||
| − | ידוע שהפ״מ מאפס את A, ולכן נסיק שהפ״מ זהה לפ״א. מכאן אפשר לומר שגודל הבלוק הגדול ביותר המתאים לע״ע 1 הוא 3. אבל A היא כבר מסדר 3x3 ולכן זהו הבלוק היחיד בצורת ז׳ורדן שלה. לכן צורת ז׳ורדן היא <math>J_1(3)</math>. | + | (החישוב האחרון ברור גם ממשפט קיילי-המילטון, שכן הצבנו את <math>A</math> לפ"א שלה). |
| + | |||
| + | |||
| + | ידוע שהפ״מ מאפס את A, והראינו שכל שאר האפשרויות לפ"מ לא מאפסות את A, ולכן נסיק שהפ״מ זהה לפ״א. מכאן אפשר לומר שגודל הבלוק הגדול ביותר המתאים לע״ע 1 הוא 3. אבל A היא כבר מסדר 3x3 ולכן זהו הבלוק היחיד בצורת ז׳ורדן שלה. לכן צורת ז׳ורדן היא <math>J_1(3)</math>. | ||
סיימנו את התרגיל. | סיימנו את התרגיל. | ||
| שורה 46: | שורה 56: | ||
---- | ---- | ||
| − | + | מכיוון שכבר כתבתי וחבל לי למחוק, נראה כעת נימוק יותר אלמנטרי: | |
גרסה אחרונה מ־16:54, 27 בדצמבר 2011
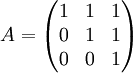
נסמן את סדר המטריצה  ב-
ב-  .
.
נמצא פ"א: 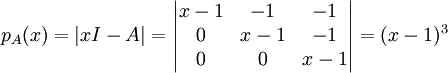 כי דטר' של מטר' משולשית היא מכפלת איברי האלכסון.
כי דטר' של מטר' משולשית היא מכפלת איברי האלכסון.
נראה שזהו גם הפ"מ של A:
הפ"מ מחלק את הפ"א, והחזקה הn-ית (כאן 3) של הפ"מ מתחלקת בפ״א. לכן הפ"מ חייב להיות מהצורה 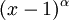 , כאשר
, כאשר 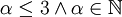 .
.
ברור 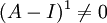 .
.
נבדוק ישירות שA-I בריבוע שונה ממטריצת אפסים: 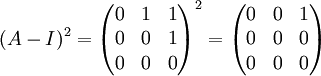
אבל 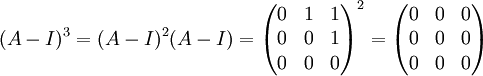
(החישוב האחרון ברור גם ממשפט קיילי-המילטון, שכן הצבנו את  לפ"א שלה).
לפ"א שלה).
ידוע שהפ״מ מאפס את A, והראינו שכל שאר האפשרויות לפ"מ לא מאפסות את A, ולכן נסיק שהפ״מ זהה לפ״א. מכאן אפשר לומר שגודל הבלוק הגדול ביותר המתאים לע״ע 1 הוא 3. אבל A היא כבר מסדר 3x3 ולכן זהו הבלוק היחיד בצורת ז׳ורדן שלה. לכן צורת ז׳ורדן היא 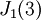 .
סיימנו את התרגיל.
.
סיימנו את התרגיל.
מכיוון שכבר כתבתי וחבל לי למחוק, נראה כעת נימוק יותר אלמנטרי:
קיבלנו שהמטריצה 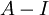 נילפ' מאינדקס 3. לכן, לפי משפט שהוכחנו, הבלוק הגדול ביותר בצורת ז'ורדן שדומה לה הוא מסדר 3=אינדקס הנילפוטנטיות.
אבל המטר' היא כבר מסדר 3, ולכן בלוק זה חייב להיות הבלוק היחיד במטריצה. קיבלנו ש
נילפ' מאינדקס 3. לכן, לפי משפט שהוכחנו, הבלוק הגדול ביותר בצורת ז'ורדן שדומה לה הוא מסדר 3=אינדקס הנילפוטנטיות.
אבל המטר' היא כבר מסדר 3, ולכן בלוק זה חייב להיות הבלוק היחיד במטריצה. קיבלנו ש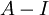 דומה לבלוק ז'ורדן נילפוטנטי מסדר 3.
דומה לבלוק ז'ורדן נילפוטנטי מסדר 3.
לפי הגדרת דמיון המטריצות, קיימת מטר' הפיכה 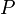 כך ש:
כך ש:
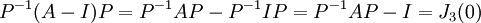
נעביר אגפים ונקבל: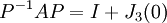
קיבלנו שצורת ז'ורדן הדומה ל-A היא 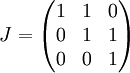
כפי שקיבלנו קודם.
כנדרש! :)