הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' עברית, תשס"ג, מועד ב, שאלה 1 בחלק III"
מ (השינוי הקטן ביותר שניתן להעלות על הדעת?) |
מ |
||
| (6 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[תחרות חנוכה לינארית 2 תשעב|חזרה]] | ||
| + | |||
'''סימון''' - <math>J_i:=J_i(0)</math>. | '''סימון''' - <math>J_i:=J_i(0)</math>. | ||
ראשית נראה שהמספר לא יכול להיות גדול מ-3, ואז נראה שניתן לבנות דוגמה של 3 מטריצות שכאלה. בכך תושלם ההוכחה. | ראשית נראה שהמספר לא יכול להיות גדול מ-3, ואז נראה שניתן לבנות דוגמה של 3 מטריצות שכאלה. בכך תושלם ההוכחה. | ||
| − | ידוע שמטריצות דומות <=> צורת ז'ורדן שלהן זהה. כאן כל שתי מטריצות שונות אינן דומות, ולכן לכל אחת מהן יש צורת ז'ורדן שונה. הן נילפוטנטיות, ולכן בצורת ז'ורדן שלהן הבלוקים המופיעים שייכים לע"ע 0 - כלומר הם בלוקים נילפוטנטיים. הבלוק יכול להיות מסדר של לכל היותר 3, והסדר חייב להיות טבעי. נוסף על כך, סכום הסדרים של הבלוקים בצורת ז'ורדן צריך להסתכם ל-3. | + | ידוע שמטריצות הן דומות <=> צורת ז'ורדן שלהן זהה. כאן כל שתי מטריצות שונות אינן דומות, ולכן לכל אחת מהן יש צורת ז'ורדן שונה. הן נילפוטנטיות, ולכן בצורת ז'ורדן שלהן הבלוקים המופיעים שייכים לע"ע 0 - כלומר הם בלוקים נילפוטנטיים. הבלוק יכול להיות מסדר של לכל היותר 3, והסדר חייב להיות טבעי. נוסף על כך, סכום הסדרים של הבלוקים בצורת ז'ורדן צריך להסתכם ל-3. |
המשימה שלנו, אם כך, היא למצוא בכמה דרכים שונות ניתן למלא מטריצת בלוקים שהיא מסדר 3 בבלוקים נילפוטנטיים. | המשימה שלנו, אם כך, היא למצוא בכמה דרכים שונות ניתן למלא מטריצת בלוקים שהיא מסדר 3 בבלוקים נילפוטנטיים. | ||
| שורה 9: | שורה 11: | ||
אם יש במטריצה בלוק מסדר 3, אזי בלוק זה חייב להיות המטריצה עצמה; לכן קיבלנו את האפשרות <math>J_3</math>. | אם יש במטריצה בלוק מסדר 3, אזי בלוק זה חייב להיות המטריצה עצמה; לכן קיבלנו את האפשרות <math>J_3</math>. | ||
| − | אם יש במטריצה בלוק מסדר 2, אזי הבלוק האחר חייב להיות מסדר 1; לכן קיבלנו את האפשרות <math>\begin{ | + | אם יש במטריצה בלוק מסדר 2, אזי הבלוק האחר חייב להיות מסדר 1; לכן קיבלנו את האפשרות <math>\begin{pmatrix} |
J_2 & \\ | J_2 & \\ | ||
& J_1 | & J_1 | ||
| − | \end{ | + | \end{pmatrix}</math>. |
האפשרות היחידה שנותרה היא שיש במטריצה בלוק מסדר 1, אבל אין בה בלוקים מסדר 2 ו-3. כלומר קיבלנו את האפשרות <math>\begin{pmatrix} | האפשרות היחידה שנותרה היא שיש במטריצה בלוק מסדר 1, אבל אין בה בלוקים מסדר 2 ו-3. כלומר קיבלנו את האפשרות <math>\begin{pmatrix} | ||
| שורה 23: | שורה 25: | ||
| − | נותר לבנות דוגמא של 3: ניקח את המטריצות | + | נותר לבנות דוגמא של 3: ניקח את שלוש המטריצות |
| − | + | <math>\begin{pmatrix} | |
J_1 & & \\ | J_1 & & \\ | ||
& J_1 & \\ | & J_1 & \\ | ||
& & J_1 | & & J_1 | ||
| − | \end{pmatrix} | + | \end{pmatrix}. |
| − | </math>, <math>\begin{ | + | |
| + | </math>, <math>\begin{pmatrix} | ||
J_2 & \\ | J_2 & \\ | ||
& J_1 | & J_1 | ||
| − | \end{ | + | \end{pmatrix}</math>, |
| + | <math>J_3</math>. | ||
| + | |||
| + | כל אחת מהן נילפוטנטית, (קל לבדוק, אבל בגלל שכבר הובהר לי שלא רואים בעין יפה את הביטוי הזה, אפשר לומר שזה נובע ממסקנה 4 בעמוד הראשון [http://math-wiki.com/images/4/46/Hanucca_BlockDiagonal.LinearA2.2010.pdf כאן], שהרי כל אחת מהמטריצות הנ"ל היא סכום ישר של מטריצות נילפוטנטיות (במקרה של J_3 זה סכום ישר באופן לא ממש מעניין, אבל עדיין סכום ישר), | ||
| − | + | ולכן לפי המסקנה אם נעלה בחזקה של המקסימום של אינדקסי הנילפוטנטיות של הבלוקים נקבל מטריצת אפסים.]), | |
| + | ולמעשה כבר הראינו שאף שתיים מהן אינן דומות - שכן הן צורות ז'ורדן של עצמן, והן שונות אחת מהשנייה. | ||
מש"ל! | מש"ל! | ||
הערה - במהלך הפתרון הסתכלנו על צורות ז'ורדן ש(זהות עד כדי שינוי סדר בלוקים) כזהות. זה ברור, אבל אני פרנואיד וחושש שיגנבו את הפתרון הדי-יפה הזה. מאותה הסיבה, הערה מעניינת תִּמָּצא בדף השיחה של פתרון זה, לא כחלק מהפתרון עצמו. :) | הערה - במהלך הפתרון הסתכלנו על צורות ז'ורדן ש(זהות עד כדי שינוי סדר בלוקים) כזהות. זה ברור, אבל אני פרנואיד וחושש שיגנבו את הפתרון הדי-יפה הזה. מאותה הסיבה, הערה מעניינת תִּמָּצא בדף השיחה של פתרון זה, לא כחלק מהפתרון עצמו. :) | ||
גרסה אחרונה מ־11:15, 9 בינואר 2012
סימון - 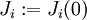 .
.
ראשית נראה שהמספר לא יכול להיות גדול מ-3, ואז נראה שניתן לבנות דוגמה של 3 מטריצות שכאלה. בכך תושלם ההוכחה.
ידוע שמטריצות הן דומות <=> צורת ז'ורדן שלהן זהה. כאן כל שתי מטריצות שונות אינן דומות, ולכן לכל אחת מהן יש צורת ז'ורדן שונה. הן נילפוטנטיות, ולכן בצורת ז'ורדן שלהן הבלוקים המופיעים שייכים לע"ע 0 - כלומר הם בלוקים נילפוטנטיים. הבלוק יכול להיות מסדר של לכל היותר 3, והסדר חייב להיות טבעי. נוסף על כך, סכום הסדרים של הבלוקים בצורת ז'ורדן צריך להסתכם ל-3.
המשימה שלנו, אם כך, היא למצוא בכמה דרכים שונות ניתן למלא מטריצת בלוקים שהיא מסדר 3 בבלוקים נילפוטנטיים.
אם יש במטריצה בלוק מסדר 3, אזי בלוק זה חייב להיות המטריצה עצמה; לכן קיבלנו את האפשרות 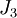 .
.
אם יש במטריצה בלוק מסדר 2, אזי הבלוק האחר חייב להיות מסדר 1; לכן קיבלנו את האפשרות 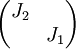 .
.
האפשרות היחידה שנותרה היא שיש במטריצה בלוק מסדר 1, אבל אין בה בלוקים מסדר 2 ו-3. כלומר קיבלנו את האפשרות 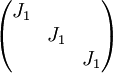 .
.
קיבלנו שמספר הדרכים השונות הוא 3, ולכן לא ייתכן שתהיינה יותר מ3 מטריצות שתצייתנה לתנאי השאלה (שכן אחרת נקבל שצורות ז'ורדן שלהן שונות, ושיש יותר מ-3, בסתירה).
נותר לבנות דוגמא של 3: ניקח את שלוש המטריצות
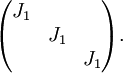 ,
, 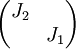 ,
,
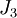 .
.
כל אחת מהן נילפוטנטית, (קל לבדוק, אבל בגלל שכבר הובהר לי שלא רואים בעין יפה את הביטוי הזה, אפשר לומר שזה נובע ממסקנה 4 בעמוד הראשון כאן, שהרי כל אחת מהמטריצות הנ"ל היא סכום ישר של מטריצות נילפוטנטיות (במקרה של J_3 זה סכום ישר באופן לא ממש מעניין, אבל עדיין סכום ישר),
ולכן לפי המסקנה אם נעלה בחזקה של המקסימום של אינדקסי הנילפוטנטיות של הבלוקים נקבל מטריצת אפסים.]), ולמעשה כבר הראינו שאף שתיים מהן אינן דומות - שכן הן צורות ז'ורדן של עצמן, והן שונות אחת מהשנייה.
מש"ל!
הערה - במהלך הפתרון הסתכלנו על צורות ז'ורדן ש(זהות עד כדי שינוי סדר בלוקים) כזהות. זה ברור, אבל אני פרנואיד וחושש שיגנבו את הפתרון הדי-יפה הזה. מאותה הסיבה, הערה מעניינת תִּמָּצא בדף השיחה של פתרון זה, לא כחלק מהפתרון עצמו. :)