הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' עברית, תשס"ד, מועד א, שאלה 11"
מתוך Math-Wiki
(יצירת דף עם התוכן "<math>A=\begin{pmatrix} 5 & 0 & 0 &0 \\ 1& 4 & 0 & 0\\ 2& 3& 3 &0 \\ 4 & 5 &6 & 3 \end{pmatrix} </math> נמצא פ"א:") |
|||
| (3 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 7: | שורה 7: | ||
</math> | </math> | ||
| − | נמצא פ"א: | + | נמצא פ"א:<math> |
| + | p_A(x)=|xI-A|=\begin{vmatrix} | ||
| + | x-5 & 0 & 0 &0 \\ | ||
| + | -1& x-4 & 0 & 0\\ | ||
| + | -2& -3&x- 3 &0 \\ | ||
| + | -4 & -5 &-6 &x- 3 | ||
| + | \end{vmatrix}=(x-5)(x-4)(x-3)^2 | ||
| + | </math> | ||
| + | |||
| + | שכן דטר' של מטר' משולשית שווה למכפלת איברי האלכסון הראשי. | ||
| + | |||
| + | הפ"א מתפרק לגורמים לינאריים, ולכן צורת ז'ורדן של A קיימת בהכרח. | ||
| + | |||
| + | כעת, נמצא את הפולינום המינימלי. | ||
| + | |||
| + | נציב את A לפול': <math>(x-5)(x-4)(x-3)</math>, ונקבל: <math>(A-5I)(A-4I)(A-3I)=\begin{pmatrix} | ||
| + | 0 & 0 & 0 &0 \\ | ||
| + | 1& -1 & 0 & 0\\ | ||
| + | 2& 3& -2 &0 \\ | ||
| + | 4 & 5 &6 & -2 | ||
| + | \end{pmatrix}\cdot \begin{pmatrix} | ||
| + | 1 & 0 & 0 &0 \\ | ||
| + | 1& 0 & 0 & 0\\ | ||
| + | 2& 3& -1 &0 \\ | ||
| + | 4 & 5 &6 & -1 | ||
| + | \end{pmatrix}\cdot \begin{pmatrix} | ||
| + | 2 & 0 & 0 &0 \\ | ||
| + | 1& 1 & 0 & 0\\ | ||
| + | 2& 3& 0 &0 \\ | ||
| + | 4 & 5 &6 & 0 | ||
| + | \end{pmatrix}=\begin{pmatrix} | ||
| + | 0 & 0& 0 & 0\\ | ||
| + | 0 & 0& 0 & 0\\ | ||
| + | 0 & 0& 0 & 0\\ | ||
| + | 6& -36 & 12& 0 | ||
| + | \end{pmatrix}</math> | ||
| + | שונה ממטריצת אפסים. לכן הפ"מ חייב להיות שווה לפ"א. | ||
| + | |||
| + | זה מספיק כדי לקבוע לנו חד-משמעית (עד כדי שינוי סדר הבלוקים) את צורת ז'ורדן של A: | ||
| + | |||
| + | <math>\begin{pmatrix} | ||
| + | J_1(5) & & \\ | ||
| + | & J_1(4) & \\ | ||
| + | & & J_2(3) | ||
| + | \end{pmatrix}=\begin{pmatrix} | ||
| + | J_1(5) & & \\ | ||
| + | & J_1(4) & \\ | ||
| + | & & J_2(3) | ||
| + | \end{pmatrix}=\begin{pmatrix} | ||
| + | 5& & & \\ | ||
| + | & 4 & & \\ | ||
| + | & &3 &1 \\ | ||
| + | & &0 &3 | ||
| + | \end{pmatrix}</math> | ||
| + | |||
| + | (המקומות הריקים הם אפסים.) | ||
גרסה אחרונה מ־15:22, 29 בדצמבר 2011
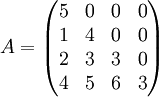
נמצא פ"א: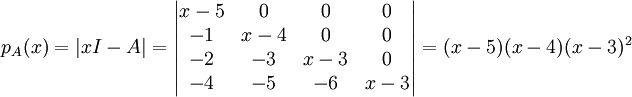
שכן דטר' של מטר' משולשית שווה למכפלת איברי האלכסון הראשי.
הפ"א מתפרק לגורמים לינאריים, ולכן צורת ז'ורדן של A קיימת בהכרח.
כעת, נמצא את הפולינום המינימלי.
נציב את A לפול':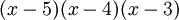 
, ונקבל: 
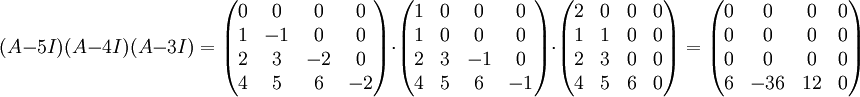שונה ממטריצת אפסים. לכן הפ"מ חייב להיות שווה לפ"א.
זה מספיק כדי לקבוע לנו חד-משמעית (עד כדי שינוי סדר הבלוקים) את צורת ז'ורדן של A:
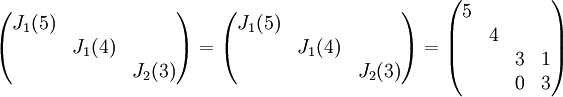
(המקומות הריקים הם אפסים.)
