פתרון לינארית 2, אונ' קנט, יוני 2010, שאלה 21
א. נתון שהפולינום האופייני של האופרטור הוא: 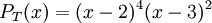 . סכום החזקות של הפולינום המינימלי של האופרטור הוא 6, ולכן צורת ז'ורדן היא מסדר 6X6. צורת זו'רדן של האופרטור תיראה מהצורה:
. סכום החזקות של הפולינום המינימלי של האופרטור הוא 6, ולכן צורת ז'ורדן היא מסדר 6X6. צורת זו'רדן של האופרטור תיראה מהצורה: 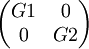 כאשר G1, G2 הם בלוקים השייכים לע"ע של האופרטור 2 ו-3 בהתאמה.
כאשר G1, G2 הם בלוקים השייכים לע"ע של האופרטור 2 ו-3 בהתאמה.
אמצא את G1, השייך לע"ע 2:
ריבוי האלגברי של הע"ע 2 בפולינום האופייני הוא 4, ולכן G1 הוא מסדר 4X4. הפולינום המינימלי של האופרטור הוא: 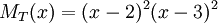 החזקה של הע"ע 2 בו הוא 2. לכן, בלוק ז'ורדן הגדול ביותר שיופיע ב-G1 הוא מסדר 2X2. כלומר, ל-G1 מספר אפשרויות:
החזקה של הע"ע 2 בו הוא 2. לכן, בלוק ז'ורדן הגדול ביותר שיופיע ב-G1 הוא מסדר 2X2. כלומר, ל-G1 מספר אפשרויות: 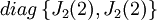 או
או 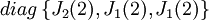 .
.
אמצא את G2, השייך לע"ע 3:
ריבוי האלגברי של הע"ע 3 בפולינום האופייני הוא 2, ולכן G2 הוא מסדר 2X2. החזקה של הע"ע 3 בפולינום המינימלי הוא גם 2, ולכן בלוק ז'ורדן הגדול ביותר שיופיע בו יהיה מסדר 2X2. ולכן, ל-G2 יש רק אפשרות אחת, והיא: 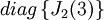
ולכן, כל צורות ז'ורדן האפשריות לאופרטור הן:
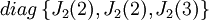 או
או 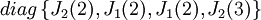 .
.
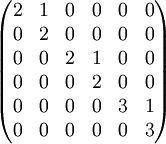 או
או 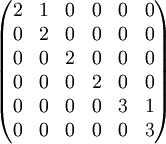
ב. הפולינום האופייני שלו הוא: 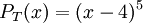 , ולכן צורת ז'ורדן היא מסדר 5X5. בנוסף, נתון ש:
, ולכן צורת ז'ורדן היא מסדר 5X5. בנוסף, נתון ש: 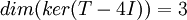 . עפ"י הנוסחא הבאה, מספר בלוקי הז'ורדן של הע"ע
. עפ"י הנוסחא הבאה, מספר בלוקי הז'ורדן של הע"ע 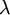 של האופרטור המופיעים בצורת ז'ורדן שלו הם:
של האופרטור המופיעים בצורת ז'ורדן שלו הם: 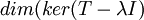 ולכן, עבור הע"ע
ולכן, עבור הע"ע 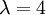 מספר בלוקי הז'ורדן הם:
מספר בלוקי הז'ורדן הם: 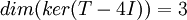 כלומר 3. מכיוון שאינינו יודעים את הריבוי האלגברי של הפולינום המינימלי, אין לדעת מהו הסדר של בלוק הז'ורדן הגדול ביותר, ולכן ישנן 2 אפשרויות:
כלומר 3. מכיוון שאינינו יודעים את הריבוי האלגברי של הפולינום המינימלי, אין לדעת מהו הסדר של בלוק הז'ורדן הגדול ביותר, ולכן ישנן 2 אפשרויות:
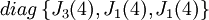 או
או 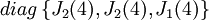 .
.
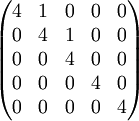 או
או 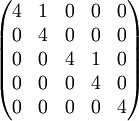
מ.ש.ל (: