קבוצה פורשת
מתוך Math-Wiki
קבוצה B של וקטורים במרחב וקטורי V מעל שדה F פורשת את המרחב, אם כל וקטור ב-v הוא צירוף לינארי (עם מקדמים מ-F) של וקטורי B.
כל קבוצה B פורשת את הקבוצה הנפרשת על-ידיה.
המקרה הסופי. נניח ש- 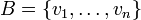 היא קבוצה סופית. אז B פורשת את V אם לכל
היא קבוצה סופית. אז B פורשת את V אם לכל 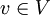 קיימים
קיימים 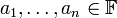 כך ש-
כך ש- 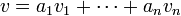 .
.
המקרה הכללי. כאשר B אינה סופית נדרשת הגדרה מעט יותר מורכבת: B פורשת את V אם לכל 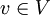 קיימים
קיימים 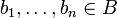 ו-
ו- 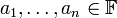 כך ש-
כך ש- 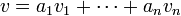 (אפשר להשתמש, כביכול, בוקטורים שונים מ-B לכל וקטור v).
(אפשר להשתמש, כביכול, בוקטורים שונים מ-B לכל וקטור v).
דוגמאות
וקטורי היחידה 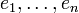 פורשים את מרחב הוקטורים
פורשים את מרחב הוקטורים 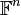 . הקבוצה
. הקבוצה 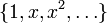 פורשת את מרחב הפולינומים
פורשת את מרחב הפולינומים ![{\mathbb F}[x]](/images/math/e/4/0/e40498a8cf322e6ba9ecfe48efb91df1.png) .
.
הקשר לבסיסים
קבוצה פורשת ובלתי תלויה היא בסיס. כל קבוצה פורשת של V מכילה בסיס. כל קבוצה המכילה בסיס היא פורשת.