שיחה:88-132 אינפי 1 סמסטר א' תשעד מדמח
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
שאלות
שתיי שאלות בנושא חסמים
1. מה צריך לקיים חסם עליון של קבוצה, שהוא גם המקסימום של הקבוצה?
2. נניח שנתונה הקבוצה הבאה:
zz A={2,3,5,8} zz
החסם העליון שלה הוא 8.
אבל משהו כאן לא ברור לי.
ע"פ הגדרת החסם העליון מתקיים ש-8 חסם מלעיל של A (עם הדרישה הזו אין לי בעיה).
אבל צריכה להתקיים דרישה נוספת, שאיתה דווקא יש בעיה...
הדרישה אומרת שלכל e>0 קיים איבר a ב-A כך ש-a > 8-e.
אבל עבור e=0.1 למשל, (ועבור אפסילונים רבים אחרים), לא קיים איבר a ב-A כך ש- a>8-e.
אם כך, הדרישה השנייה של קיום חסם עליון, אינה מתקיימת. מדוע אז 8 הוא בכל זאת חסם עליון?
- על מנת להיות מקסימום, האיבר צריך להיות שייך לקבוצה. לגבי הדוגמא שנתת, בוודאי שיש איבר a כזה. שכחת את 8 בעצמו! הרי
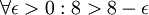
- --ארז שיינר 21:31, 23 באוקטובר 2013 (IDT)
איך מוכיחים שהמקסימום של קבוצה הוא הסופרימום של הקבוצה?
תודה
- הוכחה: נניח M הוא המקסימום של הקבוצה A, לכן ברור שהוא חסם עליון.
- נותר להוכיח, אם כן, שאין חסם עליון קטן יותר מM.
- נניח בשלילה שיש חסם עליון כזה N שקטן ממש מM.
- כיוון שM מקסימום, הוא שייך לקבוצה.
- לכן, יש איבר בקבוצה (M בעצמו) שגדול יותר מN בסתירה לכך שN הוא חסם מלעיל.
- --ארז שיינר 21:32, 23 באוקטובר 2013 (IDT)
שאלה לגבי תרגיל שמופיע באתר
אומנם מופיע גם הפתרון..אבל יש שם כמה דברים שלא מובנים לי..
השאלה הולכת כך:
יהיו קבוצות A,B מוכלות בממשיים. כל איבר ב-A קטן או שווה לכל איבר ב-B.
צריך להוכיח ש-supA<=infB.
האמת שזה די אינטואיטיבי..במיוחד אם מסתכלים על שניי תת-קטעים A , B , על הציר הממשי, שמקיימים את הנתון שכל איבר ב-A קטן שווה לכל אביר ב-B.
בסדר..מניחים בשלילה ש-supA>infB
האם נכון לומר, שמההנחה בשלילה אפשר להסיק שיש קטע (infB,supA), כך שכל איבר בקטע שייך גם לקבוצה A וגם לקבוצה B?
- לא. אין דרישה שקבוצה תכיל את כל המספרים הממשיים בקטע מסויים. קבוצות יכולות להיות אפילו סופיות. --ארז שיינר 21:34, 23 באוקטובר 2013 (IDT)
מדוע 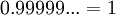
זה הוזכר גם בהרצאה וגם בתרגול ולא מובן לי בכלל למה זה נכון.
- עיקר הבעייה היא שלא למדתם כלל את הגדרת הממשיים, ולכן גם לא את הגדרת המספר
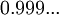 .
. - המספר אינו מוגדר על ידי הספרות שלו, אלא על ידי סכום אינסופי מהצורה
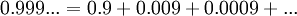
- נראה הגדרת סכום אינסופי שכזה בהמשך הקורס.
- ובכל זאת, על מנת להבין מדוע מספרים אלה שווים, אפשר לראות את ההסבר הבא:
- נסמן
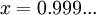 , לכן מתקיים
, לכן מתקיים 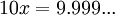
- לכן מתקיים
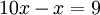
- כלומר
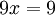
- כלומר
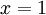 .
.
- המסקנה היא שגם לפי חוקי המתמטיקה שאתם מכירים על מספרים ממשיים, יוצא שזה אותו המספר. כאמור, אני מקווה שנבין את המספרים הממשיים טוב יותר במהלך הסמסטר.
- --ארז שיינר 21:39, 23 באוקטובר 2013 (IDT)
שאלה בחסמים
תהי 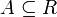 ונתון ש-
ונתון ש- 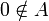 .
.
מגדירים את הקבוצה: עיבוד הנוסחה נכשל (שגיאת תחביר): A^{-1}=\left \{{1/a|a\in A}}{ \right \} .
הוכח/הפרך: אם A חסומה מלעיל, אז 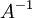 חסומה מלעיל.
חסומה מלעיל.
לדעתי הטענה לא נכונה.
למשל עבור 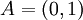 מתקיים ש-A חסומה מלעיל (למשל ע"י 3), אבל
מתקיים ש-A חסומה מלעיל (למשל ע"י 3), אבל 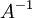 לא חסומה מלעיל.
לא חסומה מלעיל.
האינטואיציה היא שבגלל ש-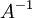 מוגדרת להיות 1 חלקי איברי A, אז עבור איברי A שקרובים ל-0, השבר מתהפך והקבוצה
מוגדרת להיות 1 חלקי איברי A, אז עבור איברי A שקרובים ל-0, השבר מתהפך והקבוצה
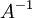 , לא תיהיה חסומה מלעיל.
, לא תיהיה חסומה מלעיל.
השאלה שלי היא כיצד אני מוכיח את זה בצורה מדוייקת.
בעצם מה שאני רוצה להראות, זה ש-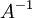 לא חסומה מלעיל. כלומר להראות שמתקיימת הטענה הבאה:
לא חסומה מלעיל. כלומר להראות שמתקיימת הטענה הבאה:
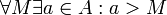 . שזו בעצם השלילה של קיום חסם מלעיל.
. שזו בעצם השלילה של קיום חסם מלעיל.
איך אני מראה את זה???
- השורה האחרונה שלך נכונה. אתה צריך להראות שלכל מספר M קיים איבר בקבוצה שגדול ממנו. איברים בקבוצה הזו הם מהצורה של אחד חלקי איברים מהקטע בין אפס לאחד.
- אז רק צריך להראות ש
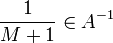 --ארז שיינר
--ארז שיינר
מה נסגר עם הנוסחאות??????????????? אני לא מצליח לראות מה אני כותב. לא הבנתי גם מה אתה כתבת כי הנוסחה לא מופיעה כמו שצריך =\