הבדלים בין גרסאות בדף "שיטות אינטגרציה"
(←ההצבה הטריגונומטרית האוניברסלית) |
|||
| שורה 79: | שורה 79: | ||
[[מדיה:09Infi2Universal.pdf|הרחבה]] | [[מדיה:09Infi2Universal.pdf|הרחבה]] | ||
| + | |||
| + | == הצבות אוילר == | ||
| + | |||
| + | הצבות אוילר מתייחסות למקרה של פונקציה "רציונאלית" אשר הרכיבים בה הם <math>x</math> ו-<math>\sqrt{ax^2+bx+c}</math>. | ||
| + | |||
| + | === אוילר 1 - הפולינום פריק === | ||
| + | |||
| + | נניח כי הפולינום <math>ax^2+bx+c</math> פריק (מעל הממשיים, כמובן). נסמן <math>ax^2+bx+c=a\left (x-\alpha\right )\left (x-\beta\right )</math>. | ||
| + | |||
| + | הצבת אוילר: נציב <math>\sqrt{ax^2+bx+c}=u\cdot\left (x-\alpha\right )</math> (אפשר גם את השורש השני). נביע את <math>x</math> באמצעות <math>u</math>, ונוכל למצוא גם את <math>x</math> וגם את <math>\sqrt{ax^2+bx+c}</math>. | ||
| + | |||
| + | ==== דוגמה ==== | ||
| + | |||
| + | <math>\int\frac{1}{x\sqrt{x^2-7x+6}}dx</math> | ||
| + | |||
| + | ניעזר בהצבת אוילר: נציב <math>\sqrt{x^2-7x+6}=u\cdot\left (x-1\right )</math>. לכן <math>\left(x-1 \right )\left(x-6 \right )=u^2\left(x-1 \right )^2</math>, כלומר <math>x-6=u^2\left(x-1 \right )</math>, ומכאן <math>x=\frac{u^2-6}{u^2-1}</math>. לכן <math>dx=\frac{2u\left (u^2-1 \right )-2u\left (u^2-6 \right )}{\left (u^2-1 \right )^2}du=\frac{10u}{\left (1-u^2 \right )^2}du</math>. בנוסף, <math>\sqrt{x^2-7x+6}=u\cdot\left ( x-1 \right )=u\cdot\left ( \frac{u^2-6}{u^2-1}-1 \right )=-\frac{5u}{u^2-1}</math> | ||
| + | |||
| + | מקבלים: | ||
| + | |||
| + | <math>\int\frac{1}{x\sqrt{x^2-7x+6}}dx=-\int\frac{1}{\ \frac{u^2-6}{u^2-1}\cdot \frac{5u}{u^2-1}\ }\cdot\frac{10u}{\left ( 1-u^2 \right )^2}du=-2\int \frac{1}{u^2-6}du</math> כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים. | ||
| + | |||
| + | === אוילר 2 - פולינום יותר כללי === | ||
| + | |||
| + | ישנן שתי אפשרויות: | ||
| + | # בהינתן <math>a>0</math>, נציב <math>\sqrt{ax^2+bx+c}=\sqrt{a}\cdot x+u</math>. | ||
| + | # בהינתן <math>c>0</math>, נציב <math>\sqrt{ax^2+bx+c}=xu+\sqrt{c}</math>. | ||
| + | |||
| + | נביע את <math>x</math> באמצעות <math>u</math>, ונוכל למצוא את <math>dx</math> ואת <math>\sqrt{ax^2+bx+c}</math>. | ||
| + | |||
| + | ==== דוגמה ==== | ||
| + | |||
| + | <math>\int\frac{1}{\sqrt{x^2-7x+6}}dx</math> | ||
| + | |||
| + | ניעזר בהצבת אוילר (האופציה הראשונה): נציב <math>\sqrt{x^2-7x+6}=x+u</math>. נעלה בריבוע ונקבל <math>x^2-7x+6=x^2+2xu+u^2</math>, כלומר <math>x=\frac{6-u^2}{2u+7}</math>. לכן <math>dx=\frac{-2u\left (2u+7 \right )-2\left (6-u^2 \right )}{\left (2u+7 \right )^2}du=-2\cdot\frac{u^2+7u+6}{\left ( 2u+7 \right )^2}du</math>, וכן <math>\sqrt{x^2-7x+6}=x+u=\frac{6-u^2}{2u+7}+u=\frac{6-u^2+2u^2+7u}{2u+7}=\frac{u^2+7u+6}{2u+7}</math>. | ||
| + | |||
| + | מקבלים: | ||
| + | |||
| + | <math>\int\frac{1}{\sqrt{x^2-7x+6}}dx=-\int\frac{1}{\ \frac{u^2+7u+6}{2u+7} \ }\cdot 2\cdot\frac{u^2+7u+6}{\left ( 2u+7 \right )^2}du=-\int\frac {2}{2u+7}du=-ln\left | 2u+7 \right |+c=-ln\left | \sqrt{x^2-7x+6}-x \right |+c</math> | ||
גרסה מ־19:23, 29 במרץ 2013
בדף זה יוצגו מספר שיטות אינטגרציה הניתנות לשימוש.
תוכן עניינים
אינטגרציה "רגילה"
הכוונה היא לבצע את האינטגרל לפי חוקי הגזירה. לדוגמה,
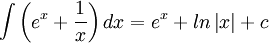 .
.
השלמה לריבוע
כאשר נקבל פונקציה רציונאלית שבמונה שלה יש מספר ובמכנה שלה פולינום ממעלה שנייה, ניתן להשלים את הפולינום לריבוע ולהיעזר ב-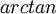 .
.
דוגמה
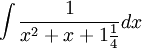
ניעזר בהשלמה לריבוע של המכנה. נקבל:
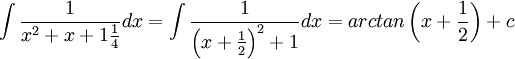
אינטגרציה בחלקים
לפי נוסחת הגזירה של מכפלת פונקציות (נוסחת לייבניץ), אנו מקבלים:
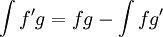 (ניתן לוודא על ידי גזירה).
(ניתן לוודא על ידי גזירה).
דוגמה
נחפש את 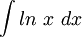 .
.
לפי השיטה, נסמן 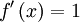 ,
, 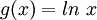 .
.
לכן נקבל 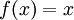 ,
, 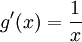 .
.
לפי נוסחת אינטגרציה בחלקים, נקבל:
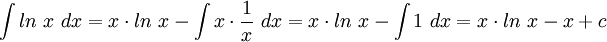 .
.
הרחבה
אינטגרציה בהצבה
לפי כלל השרשרת, אנו מקבלים:
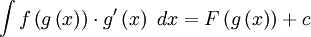 (ניתן לוודא על ידי גזירה).
(ניתן לוודא על ידי גזירה).
דוגמה
נחפש את 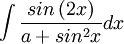 כאשר
כאשר 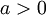 .
.
נבצע הצבה: 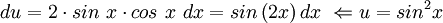 . מקבלים:
. מקבלים:
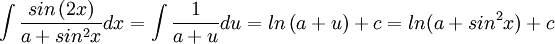 (נזכור כי
(נזכור כי 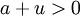 , לכן אין צורך בערך מוחלט).
, לכן אין צורך בערך מוחלט).
הרחבה
ההצבה הטריגונומטרית האוניברסלית
בהינתן פונקציה אשר משולבות בה פונקציות טריגונומטריות (ועדיף שהיא תהיה מנה של חיבור וכפל שלהן), אזי נציב 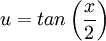 .
.
נזכור כי 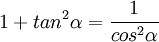 , ונקבל
, ונקבל 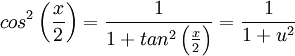 .
.
נקבל בנוסף 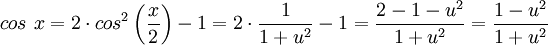 .
.
לכן 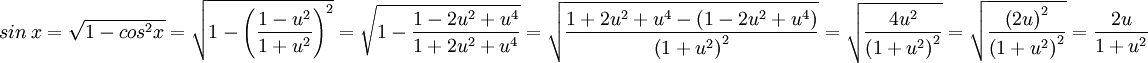
כמו כן, 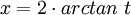 , ולכן
, ולכן 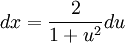 .
.
דוגמה
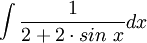
ניעזר בהצבה הטריגונומטרית האוניברסלית. נציב 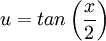 . נקבל:
. נקבל:
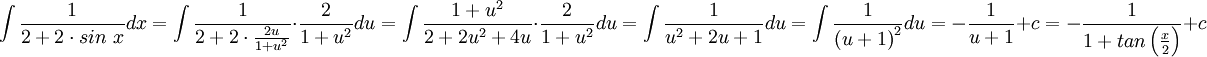
הרחבה
הצבות אוילר
הצבות אוילר מתייחסות למקרה של פונקציה "רציונאלית" אשר הרכיבים בה הם  ו-
ו-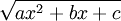 .
.
אוילר 1 - הפולינום פריק
נניח כי הפולינום 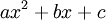 פריק (מעל הממשיים, כמובן). נסמן
פריק (מעל הממשיים, כמובן). נסמן 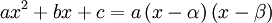 .
.
הצבת אוילר: נציב 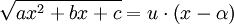 (אפשר גם את השורש השני). נביע את
(אפשר גם את השורש השני). נביע את  באמצעות
באמצעות 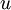 , ונוכל למצוא גם את
, ונוכל למצוא גם את  וגם את
וגם את 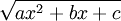 .
.
דוגמה
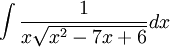
ניעזר בהצבת אוילר: נציב 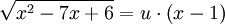 . לכן
. לכן 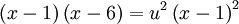 , כלומר
, כלומר 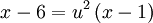 , ומכאן
, ומכאן 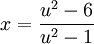 . לכן
. לכן 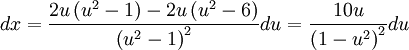 . בנוסף,
. בנוסף, 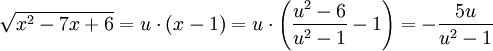
מקבלים:
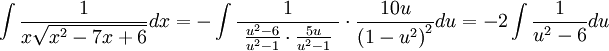 כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים.
כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים.
אוילר 2 - פולינום יותר כללי
ישנן שתי אפשרויות:
- בהינתן
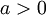 , נציב
, נציב 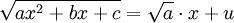 .
. - בהינתן
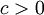 , נציב
, נציב 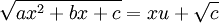 .
.
נביע את  באמצעות
באמצעות 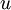 , ונוכל למצוא את
, ונוכל למצוא את 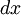 ואת
ואת 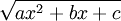 .
.
דוגמה
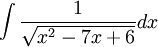
ניעזר בהצבת אוילר (האופציה הראשונה): נציב 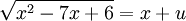 . נעלה בריבוע ונקבל
. נעלה בריבוע ונקבל 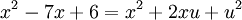 , כלומר
, כלומר 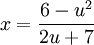 . לכן
. לכן 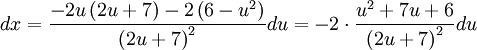 , וכן
, וכן 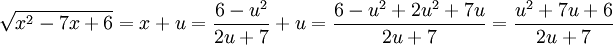 .
.
מקבלים: