הבדלים בין גרסאות בדף "שיטות אינטגרציה"
Ofekgillon10 (שיחה | תרומות) (←ההצבה הטריגונומטרית האוניברסלית) |
|||
| שורה 4: | שורה 4: | ||
הכוונה היא לבצע את האינטגרל לפי חוקי הגזירה. לדוגמה, <BR> | הכוונה היא לבצע את האינטגרל לפי חוקי הגזירה. לדוגמה, <BR> | ||
| − | <math>\int \left(e^x+\frac{1}{x} \right )dx=e^x+ln\left | x \right |+c</math>. | + | <math>\int \left(e^x+\frac{1}{x} \right )dx=e^x+\ln\left | x \right |+c</math>. |
=== דף אינטגרלים === | === דף אינטגרלים === | ||
| שורה 12: | שורה 12: | ||
=== השלמה לריבוע === | === השלמה לריבוע === | ||
| − | כאשר נקבל פונקציה רציונאלית שבמונה שלה יש מספר ובמכנה שלה פולינום ממעלה שנייה, ניתן להשלים את הפולינום לריבוע ולהיעזר ב-<math>arctan</math>. | + | כאשר נקבל פונקציה רציונאלית שבמונה שלה יש מספר ובמכנה שלה פולינום ממעלה שנייה, ניתן להשלים את הפולינום לריבוע ולהיעזר ב-<math>\arctan</math>. |
==== דוגמה ==== | ==== דוגמה ==== | ||
| שורה 20: | שורה 20: | ||
ניעזר בהשלמה לריבוע של המכנה. נקבל: | ניעזר בהשלמה לריבוע של המכנה. נקבל: | ||
| − | <math>\int\frac{1}{x^2+x+1\frac{1}{4}}dx=\int\frac{1}{\left (x+\frac{1}{2} \right )^2+1}dx=arctan\left (x+\frac{1}{2} \right )+c</math> | + | <math>\int\frac{1}{x^2+x+1\frac{1}{4}}dx=\int\frac{1}{\left (x+\frac{1}{2} \right )^2+1}dx=\arctan\left (x+\frac{1}{2} \right )+c</math> |
== אינטגרציה בחלקים == | == אינטגרציה בחלקים == | ||
| שורה 29: | שורה 29: | ||
=== דוגמה === | === דוגמה === | ||
| − | נחפש את <math>\int ln\ x \ dx</math>. | + | נחפש את <math>\int \ln\ x \ dx</math>. |
| − | לפי השיטה, נסמן <math>f'\left (x \right )=1</math>, <math>g(x)=ln\ x</math>. | + | לפי השיטה, נסמן <math>f'\left (x \right )=1</math>, <math>g(x)=\ln\ x</math>. |
לכן נקבל <math>f(x)=x</math>, <math>g'(x)=\frac{1}{x}</math>. | לכן נקבל <math>f(x)=x</math>, <math>g'(x)=\frac{1}{x}</math>. | ||
| שורה 37: | שורה 37: | ||
לפי נוסחת אינטגרציה בחלקים, נקבל: | לפי נוסחת אינטגרציה בחלקים, נקבל: | ||
| − | <math>\int ln\ x \ dx=x\cdot ln\ x-\int x\cdot \frac{1}{x}\ dx=x\cdot ln\ x-\int 1\ dx=x\cdot ln\ x-x+c</math>. | + | <math>\int \ln\ x \ dx=x\cdot \ln\ x-\int x\cdot \frac{1}{x}\ dx=x\cdot \ln\ x-\int 1\ dx=x\cdot \ln\ x-x+c</math>. |
=== הרחבה === | === הרחבה === | ||
| שורה 50: | שורה 50: | ||
=== דוגמה === | === דוגמה === | ||
| − | נחפש את <math>\int \frac{sin\left(2x \right )}{a+sin^2 x}dx</math> כאשר <math>a>0</math>. | + | נחפש את <math>\int \frac{\sin\left(2x \right )}{a+\sin^2 x}dx</math> כאשר <math>a>0</math>. |
| − | נבצע הצבה: <math>du=2\cdot sin\ x\cdot cos\ x\ dx=sin\left(2x \right )dx \ \Leftarrow u=sin^2 x</math>. מקבלים: | + | נבצע הצבה: <math>du=2\cdot \sin\ x\cdot \cos\ x\ dx=\sin\left(2x \right )dx \ \Leftarrow u=\sin^2 x</math>. מקבלים: |
| − | <math>\int \frac{sin\left(2x \right )}{a+sin^2 x}dx=\int \frac{1}{a+u}du=ln\left ( a+u \right )+c=ln(a+sin^2 x)+c</math> (נזכור כי <math>a+u>0</math>, לכן אין צורך בערך מוחלט). | + | <math>\int \frac{\sin\left(2x \right )}{a+\sin^2 x}dx=\int \frac{1}{a+u}du=\ln\left ( a+u \right )+c=\ln(a+\sin^2 x)+c</math> (נזכור כי <math>a+u>0</math>, לכן אין צורך בערך מוחלט). |
=== הרחבה === | === הרחבה === | ||
| שורה 62: | שורה 62: | ||
== ההצבה הטריגונומטרית האוניברסלית == | == ההצבה הטריגונומטרית האוניברסלית == | ||
| − | בהינתן פונקציה אשר משולבות בה פונקציות טריגונומטריות (ועדיף שהיא תהיה מנה של חיבור וכפל שלהן), אזי נציב <math>u=tan\left (\frac{x}{2}\right )</math>. | + | בהינתן פונקציה אשר משולבות בה פונקציות טריגונומטריות (ועדיף שהיא תהיה מנה של חיבור וכפל שלהן), אזי נציב <math>u=\tan\left (\frac{x}{2}\right )</math>. |
| − | נזכור כי <math>1+tan^2\alpha=\frac{1}{cos^2 \alpha}</math>, ונקבל <math>cos^2 \left ( \frac{x}{2} \right )=\frac{1}{1+tan^2\left ( \frac{x}{2} \right )}=\frac{1}{1+u^2}</math>. | + | נזכור כי <math>1+\tan^2\alpha=\frac{1}{\cos^2 \alpha}</math>, ונקבל <math>\cos^2 \left ( \frac{x}{2} \right )=\frac{1}{1+\tan^2\left ( \frac{x}{2} \right )}=\frac{1}{1+u^2}</math>. |
| − | נקבל בנוסף <math>cos\ x=2\cdot cos^2\left ( \frac{x}{2} \right )-1=2\cdot\frac{1}{1+u^2}-1=\frac{2-1-u^2}{1+u^2}=\frac{1-u^2}{1+u^2}</math>. | + | נקבל בנוסף <math>\cos\ x=2\cdot \cos^2\left ( \frac{x}{2} \right )-1=2\cdot\frac{1}{1+u^2}-1=\frac{2-1-u^2}{1+u^2}=\frac{1-u^2}{1+u^2}</math>. |
| − | לכן <math>sin\ x=\sqrt{ 1-cos^2 x }=\sqrt{1-\left (\frac{1-u^2}{1+u^2} \right )^2}=\sqrt{1-\frac{1-2u^2+u^4}{1+2u^2+u^4}}=\sqrt{\frac{1+2u^2+u^4-\left (1-2u^2+u^4 \right )}{\left ( 1+u^2 \right )^2}}=\sqrt{\frac{4u^2}{\left ( 1+u^2 \right )^2}}=\sqrt{\frac{\left ( 2u \right )^2}{\left ( 1+u^2 \right )^2}}=\frac{2u}{1+u^2}</math> | + | לכן <math>\sin\ x=\sqrt{ 1-\cos^2 x }=\sqrt{1-\left (\frac{1-u^2}{1+u^2} \right )^2}=\sqrt{1-\frac{1-2u^2+u^4}{1+2u^2+u^4}}=\sqrt{\frac{1+2u^2+u^4-\left (1-2u^2+u^4 \right )}{\left ( 1+u^2 \right )^2}}=\sqrt{\frac{4u^2}{\left ( 1+u^2 \right )^2}}=\sqrt{\frac{\left ( 2u \right )^2}{\left ( 1+u^2 \right )^2}}=\frac{2u}{1+u^2}</math> |
| − | כמו כן, <math>x=2\cdot arctan\ u</math>, ולכן <math>dx=\frac{2}{1+u^2} du</math>. | + | כמו כן, <math>x=2\cdot \arctan\ u</math>, ולכן <math>dx=\frac{2}{1+u^2} du</math>. |
=== דוגמה === | === דוגמה === | ||
| − | <math>\int\frac{1}{2+2\cdot sin\ x}dx</math> | + | <math>\int\frac{1}{2+2\cdot \sin\ x}dx</math> |
| − | ניעזר בהצבה הטריגונומטרית האוניברסלית. נציב <math>u=tan\left (\frac{x}{2}\right )</math>. נקבל: | + | ניעזר בהצבה הטריגונומטרית האוניברסלית. נציב <math>u=\tan\left (\frac{x}{2}\right )</math>. נקבל: |
| − | <math>\int\frac{1}{2+2\cdot sin\ x}dx=\int\frac{1}{2+2\cdot \frac{2u}{1+u^2}}\cdot \frac{2}{1+u^2}du=\int\frac{1+u^2}{2+2u^2+4u}\cdot\frac{2}{1+u^2}du=\int\frac{1}{u^2+2u+1}du=\int\frac{1}{\left (u+1\right )^2}du=-\frac{1}{u+1}+c=-\frac{1}{1+tan\left (\frac{x}{2}\right )}+c</math> | + | <math>\int\frac{1}{2+2\cdot \sin\ x}dx=\int\frac{1}{2+2\cdot \frac{2u}{1+u^2}}\cdot \frac{2}{1+u^2}du=\int\frac{1+u^2}{2+2u^2+4u}\cdot\frac{2}{1+u^2}du=\int\frac{1}{u^2+2u+1}du=\int\frac{1}{\left (u+1\right )^2}du=-\frac{1}{u+1}+c=-\frac{1}{1+\tan\left (\frac{x}{2}\right )}+c</math> |
=== הרחבה === | === הרחבה === | ||
| שורה 136: | שורה 136: | ||
קיימים מספר מצבים עבור פונקציות רציונאליות <math>f\left (x\right )=\frac{p(x)}{q(x)}</math> (כאשר <math>p(x),q(x)</math> פולינומים). להלן חמישה: | קיימים מספר מצבים עבור פונקציות רציונאליות <math>f\left (x\right )=\frac{p(x)}{q(x)}</math> (כאשר <math>p(x),q(x)</math> פולינומים). להלן חמישה: | ||
| − | === מצב ראשון <math>deg\ p=deg\ q-1</math> === | + | === מצב ראשון <math>\deg\ p=\deg\ q-1</math> === |
| − | במצב כזה, <math>deg\ q'=deg\ p</math>, לכן קיים קבוע <math>c</math> שעבורו <math>h=cp-q'</math> יהיה ממעלה יותר נמוכה, כלומר <math>deg\ h<\ deg\ q-1</math>. נקבל: | + | במצב כזה, <math>\deg\ q'=\deg\ p</math>, לכן קיים קבוע <math>c</math> שעבורו <math>h=cp-q'</math> יהיה ממעלה יותר נמוכה, כלומר <math>\deg\ h<\ \deg\ q-1</math>. נקבל: |
| − | <math>\int f=\int\frac{p}{q}=\int\frac{\ \frac{h+q'}{c}\ }{q}=\frac{1}{c}\cdot\int\frac{h}{q}+\frac{1}{c}\cdot ln|q|</math>. עוברים למצב הבא. | + | <math>\int f=\int\frac{p}{q}=\int\frac{\ \frac{h+q'}{c}\ }{q}=\frac{1}{c}\cdot\int\frac{h}{q}+\frac{1}{c}\cdot \ln|q|</math>. עוברים למצב הבא. |
| − | === מצב שני <math>deg\ p<deg\ q-1</math> === | + | === מצב שני <math>\deg\ p<\deg\ q-1</math> === |
מפרקים לשברים חלקיים כפי שמוסבר בקובץ [[מדיה:שברים חלקיים.pdf|הזה]]. | מפרקים לשברים חלקיים כפי שמוסבר בקובץ [[מדיה:שברים חלקיים.pdf|הזה]]. | ||
| − | === מצב שלישי <math>deg\ p\ge deg\ q</math> === | + | === מצב שלישי <math>\deg\ p\ge \deg\ q</math> === |
מבצעים חילוק פולינומים וחוזרים למצבים הקודמים. | מבצעים חילוק פולינומים וחוזרים למצבים הקודמים. | ||
גרסה מ־09:27, 18 ביולי 2014
בדף זה יוצגו מספר שיטות אינטגרציה הניתנות לשימוש. בסיום הדף מצורף קובץ המסכם את מה שנכתב כאן.
תוכן עניינים
אינטגרציה "רגילה"
הכוונה היא לבצע את האינטגרל לפי חוקי הגזירה. לדוגמה,
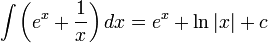 .
.
דף אינטגרלים
השלמה לריבוע
כאשר נקבל פונקציה רציונאלית שבמונה שלה יש מספר ובמכנה שלה פולינום ממעלה שנייה, ניתן להשלים את הפולינום לריבוע ולהיעזר ב-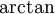 .
.
דוגמה
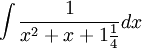
ניעזר בהשלמה לריבוע של המכנה. נקבל:
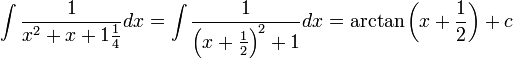
אינטגרציה בחלקים
לפי נוסחת הגזירה של מכפלת פונקציות (נוסחת לייבניץ), אנו מקבלים:
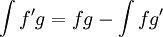 (ניתן לוודא על ידי גזירה).
(ניתן לוודא על ידי גזירה).
דוגמה
נחפש את 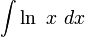 .
.
לפי השיטה, נסמן 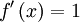 ,
, 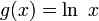 .
.
לכן נקבל 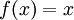 ,
, 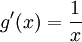 .
.
לפי נוסחת אינטגרציה בחלקים, נקבל:
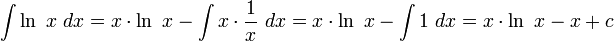 .
.
הרחבה
אינטגרציה בהצבה
לפי כלל השרשרת, אנו מקבלים:
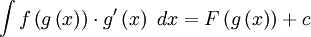 (ניתן לוודא על ידי גזירה).
(ניתן לוודא על ידי גזירה).
דוגמה
נחפש את 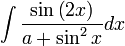 כאשר
כאשר 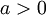 .
.
נבצע הצבה: 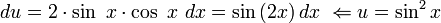 . מקבלים:
. מקבלים:
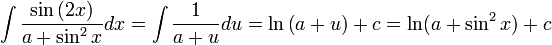 (נזכור כי
(נזכור כי 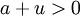 , לכן אין צורך בערך מוחלט).
, לכן אין צורך בערך מוחלט).
הרחבה
ההצבה הטריגונומטרית האוניברסלית
בהינתן פונקציה אשר משולבות בה פונקציות טריגונומטריות (ועדיף שהיא תהיה מנה של חיבור וכפל שלהן), אזי נציב 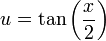 .
.
נזכור כי 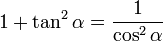 , ונקבל
, ונקבל 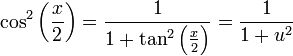 .
.
נקבל בנוסף 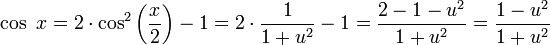 .
.
לכן 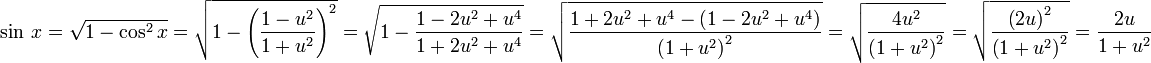
כמו כן, 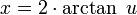 , ולכן
, ולכן 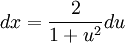 .
.
דוגמה
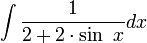
ניעזר בהצבה הטריגונומטרית האוניברסלית. נציב 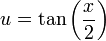 . נקבל:
. נקבל:
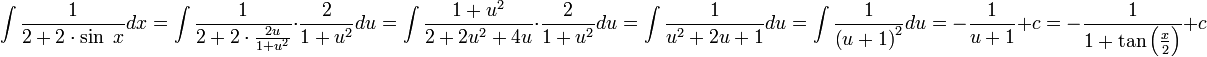
הרחבה
פירוק לשברים חלקיים
כאשר נקבל פונקציה רציונאלית שבמונה שלה פולינום ממעלה נמוכה מאשר במכנה שלה, נרצה לפרק את השבר לשברים חלקיים אשר סכומם הוא השבר המקורי, וקל לבצע אינטגרל לכל אחד מהם בנפרד. ננסה לפרק אותו לגורמים לינאריים ולגורמים ממעלה שנייה.
הצבות אוילר
הצבות אוילר מתייחסות למקרה של פונקציה "רציונאלית" אשר הרכיבים בה הם  ו-
ו-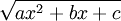 .
.
אוילר 1 - הפולינום פריק
נניח כי הפולינום 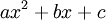 פריק (מעל הממשיים, כמובן). נסמן
פריק (מעל הממשיים, כמובן). נסמן 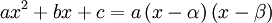 .
.
הצבת אוילר: נציב 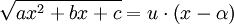 (אפשר גם את השורש השני). נביע את
(אפשר גם את השורש השני). נביע את  באמצעות
באמצעות 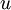 , ונוכל למצוא גם את
, ונוכל למצוא גם את  וגם את
וגם את 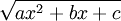 .
.
דוגמה
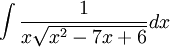
ניעזר בהצבת אוילר: נציב 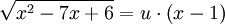 . לכן
. לכן 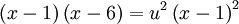 , כלומר
, כלומר 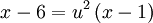 , ומכאן
, ומכאן 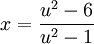 . לכן
. לכן 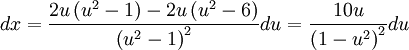 . בנוסף,
. בנוסף, 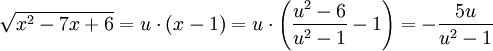
מקבלים:
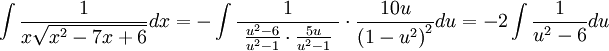 כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים.
כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים.
אוילר 2 - פולינום יותר כללי
ישנן שתי אפשרויות:
- בהינתן
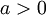 , נציב
, נציב 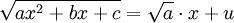 .
. - בהינתן
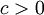 , נציב
, נציב 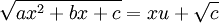 .
.
נביע את  באמצעות
באמצעות 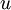 , ונוכל למצוא את
, ונוכל למצוא את 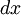 ואת
ואת 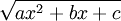 .
.
דוגמה
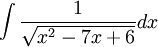
ניעזר בהצבת אוילר (האופציה הראשונה): נציב 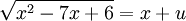 . נעלה בריבוע ונקבל
. נעלה בריבוע ונקבל 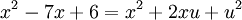 , כלומר
, כלומר 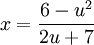 . לכן
. לכן 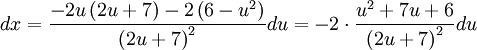 , וכן
, וכן 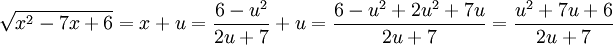 .
.
מקבלים:
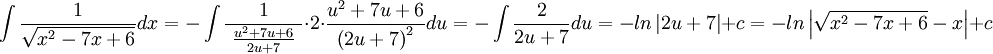
הרחבה
פונקציה רציונאלית
קיימים מספר מצבים עבור פונקציות רציונאליות 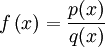 (כאשר
(כאשר 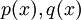 פולינומים). להלן חמישה:
פולינומים). להלן חמישה:
מצב ראשון 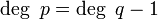
במצב כזה, 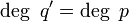 , לכן קיים קבוע
, לכן קיים קבוע 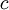 שעבורו
שעבורו 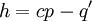 יהיה ממעלה יותר נמוכה, כלומר
יהיה ממעלה יותר נמוכה, כלומר 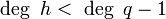 . נקבל:
. נקבל:
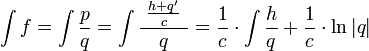 . עוברים למצב הבא.
. עוברים למצב הבא.
מצב שני 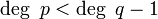
מפרקים לשברים חלקיים כפי שמוסבר בקובץ הזה.
מצב שלישי 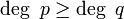
מבצעים חילוק פולינומים וחוזרים למצבים הקודמים.