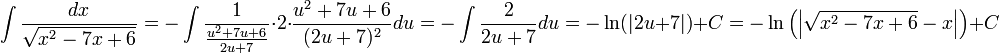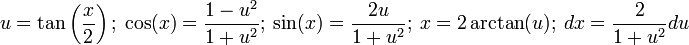הבדלים בין גרסאות בדף "שיטות אינטגרציה"
(←אינטגרציה "רגילה") |
Evyatar531 (שיחה | תרומות) מ (another way to express sin(x) as a result of the universal trigonometric substitution) |
||
| (33 גרסאות ביניים של 4 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| − | בדף זה יוצגו מספר שיטות אינטגרציה הניתנות לשימוש. | + | בדף זה יוצגו מספר שיטות אינטגרציה הניתנות לשימוש. בסיום הדף מצורף קובץ המסכם את מה שנכתב כאן. |
| − | == אינטגרציה | + | ==אינטגרציה מיידית== |
| + | אינטגרל מיידי הוא אינטגרל על פונקציה שאנחנו יודעים מי הקדומה שלה. | ||
| − | + | לדוגמא: <math>\int\left(e^x+\frac{1}{x}\right)dx=e^x+\ln(|x|)+C</math> | |
| − | <math>\int \left(e^x+\frac{1}{x} \right )dx=e^x+ln | + | |
| − | + | [[מדיה:אינטגרלים.pdf|דף אינטגרליים מיידיים]] | |
| − | + | ==אינטגרציה בחלקים== | |
| + | לפי נוסחת הגזירה של מכפלת פונקציות (נוסחת לייבניץ), אנו מקבלים: | ||
| − | = | + | <math>\int f'g=f\cdot g-\int fg'</math> (ניתן לוודא על ידי גזירה). |
| − | <math>\int\ | + | ===דוגמא=== |
| + | <math>\int\ln(x)dx</math> | ||
| − | + | לפי השיטה, נסמן <math>f'(x)=1\ ,\ g(x)=\ln(x)</math> . | |
| − | <math> | + | לכן נקבל <math>f(x)=x\ ,\ g'(x)=\frac{1}{x}</math> . |
| − | + | לפי נוסחת אינטגרציה בחלקים, נקבל: | |
| − | + | <math>\int\ln(x)dx=x\ln(x)-\int x\cdot\frac{1}{x}dx=x\ln(x)-\int 1\,dx=x\ln(x)-x+C</math> | |
| − | <math>\int | + | |
| − | |||
| − | + | [[אינטגרציה בחלקים|הרחבה]] | |
| − | + | ==אינטגרציה בהצבה== | |
| + | לפי כלל השרשרת, אנו מקבלים: | ||
| − | + | <math>\int f(g(x))\cdot g'(x)dx=F(g(x))+C</math> (ניתן לוודא על-ידי גזירה). | |
| − | + | ===דוגמא=== | |
| + | <math>\int\frac{\sin(2x)}{a+\sin^2(x)}dx</math> כאשר <math>a>0</math> . | ||
| − | <math>\ | + | נבצע הצבה<math>u=\sin^2(x)\</math> ולכן <math>du=2\sin(x)\cos(x)dx=\sin(2x)dx\</math> |
| − | + | מקבלים: | |
| − | + | <math>\int\frac{\sin(2x)}{a+\sin^2(x)}dx=\int\frac{du}{a+u}=\ln(a+u)+C=\ln\big(a+\sin^2(x)\big)+C</math> (נזכור כי <math>a+u>0</math> , לכן אין צורך בערך מוחלט). | |
| − | |||
| − | + | [[שיטת ההצבה|הרחבה]] | |
| − | + | ||
| − | == | + | ==פונקציה רציונאלית== |
| + | על מנת לחשב אינטגרל על פונקציה רציונאלית <math>f(x)=\frac{p(x)}{q(x)}</math> (כאשר <math>p(x),q(x)</math> פולינומים), עלינו לעקוב אחרי השלבים הבאים: | ||
| + | *אם דרגת המונה גדולה מדרגת המכנה, נבצע חילוק פולינומים. | ||
| + | *נבצע פירוק לשברים חלקיים. | ||
| + | *נחשב את האינטגרל של כל שבר חלקי. | ||
| − | + | ניתן לקרוא [[אלגוריתם לביצוע אינטגרל על פונקציה רציונאלית|כאן]] את האלגוריתם המלא. | |
| − | + | ==הצבות אוניברסאליות== | |
| + | '''הצבות אוניברסאליות''' הוא כינוי כללי להצבות המעבירות פונקציות ממשפחה מסוימת לצורה של [[אלגוריתם לביצוע אינטגרל על פונקציה רציונאלית|פונקציה רציונאלית]] אותה אנחנו יודעים לפתור. שימו לב שכיון ופתרון פונקציה רציונאלית דורש פירוק פולינומים, לעתים המעבר לפונקציה רציונאלית לא יקדם אותנו לקראת פתרון הבעיה. | ||
| − | + | הצבות אוניברסאליות ידועות ניתן למצוא בקובץ הבא: (עד אשר מישהו יקליד אותו אל תוך הויקי...) | |
| − | + | *[[מדיה:09Infi2Universal.pdf|הסבר על הצבות אוניברסאליות]] | |
| − | + | ==ההצבה הטריגונומטרית האוניברסלית== | |
| + | בהינתן פונקציה אשר משולבות בה פונקציות טריגונומטריות (ועדיף שהיא תהיה מנה של חיבור וכפל שלהן), אזי נציב <math>u=\tan\left(\frac{x}{2}\right)</math> . | ||
| − | == | + | נזכור כי <math>1+\tan^2(\alpha)=\frac{1}{\cos^2(\alpha)}</math> , ונקבל <math>\cos^2\left(\frac{x}{2}\right)=\frac{1}{1+\tan^2\left(\frac{x}{2}\right)}=\frac{1}{1+u^2}</math> . |
| − | + | נקבל בנוסף <math>\cos(x)=2\cos^2\left(\frac{x}{2}\right)-1=\frac{2}{1+u^2}-1=\frac{2-1-u^2}{1+u^2}=\frac{1-u^2}{1+u^2}</math> . | |
| − | + | לכן: | |
| − | + | <math>\sin(x)=\sqrt{1-\cos^2(x)}=\sqrt{1-\left(\frac{1-u^2}{1+u^2}\right)^2}=\sqrt{1-\frac{1-2u^2+u^4}{1+2u^2+u^4}}=</math> | |
| − | + | <math>\sqrt{\frac{1+2u^2+u^4-(1-2u^2+u^4)}{(1+u^2)^2}}=\sqrt{\frac{4u^2}{(1+u^2)^2}}=\sqrt{\frac{(2u)^2}{(1+u^2)^2}}=\frac{2u}{1+u^2}</math> | |
| − | + | ובדרך אחרת: | |
| − | === | + | <math>\tan(\frac{x}{2})=\frac{\sin(\frac{x}{2})}{\cos(\frac{x}{2})}=\frac{2 \cdot \sin(\frac{x}{2}) \cdot \cos(\frac{x}{2})}{2 \cos^2(\frac{x}{2})}=\frac{\sin(x)}{2 \cos^2(\frac{x}{2})}</math> |
| − | + | ולכן מתקיים | |
| − | + | <math>\sin(x)=\tan(\frac{x}{2})\cdot 2 \cos^2(\frac{x}{2})=\frac{2u}{1+u^2}</math> | |
| − | |||
| − | === | + | כמו כן, <math>x=2\arctan(u)\ \Rightarrow\ dx=\frac{2}{1+u^2}du</math> . |
| + | |||
| + | לסיכום, | ||
| + | <math>u=\tan\left(\frac{x}{2}\right);\ \cos(x)=\frac{1-u^2}{1+u^2};\ \sin(x)=\frac{2u}{1+u^2};\ x=2\arctan(u);\ dx=\frac{2}{1+u^2}du</math> | ||
| + | |||
| + | ===דוגמא=== | ||
| + | <math>\int\frac{dx}{2+2\sin(x)}</math> | ||
| + | |||
| + | נעזר בהצבה הטריגונומטרית האוניברסלית. נציב <math>u=\tan\left(\frac{x}{2}\right)</math> . נקבל: | ||
| + | |||
| + | <math>\int\frac{dx}{2+2\sin(x)}=\frac{1}{2}\int\frac{1}{1+\frac{2u}{1+u^2}}\cdot\frac{2}{1+u^2}du=\frac{1}{2}\int\frac{1+u^2}{u^2+2u+1}\cdot\frac{2}{1+u^2}du</math> | ||
| + | |||
| + | <math>=\int\frac{du}{(u+1)^2}=-\frac{1}{u+1}+C=-\frac{1}{1+\tan\left(\frac{x}{2}\right)}+C</math> | ||
| + | |||
[[מדיה:09Infi2Universal.pdf|הרחבה]] | [[מדיה:09Infi2Universal.pdf|הרחבה]] | ||
| + | |||
| + | ==הצבות אוילר== | ||
| + | הצבות אוילר מתייחסות למקרה של פונקציה "רציונאלית" אשר הרכיבים בה הם <math>x</math> ו- <math>\sqrt{ax^2+bx+c}</math> . | ||
| + | |||
| + | ===אוילר 1 - הפולינום פריק=== | ||
| + | נניח כי הפולינום <math>ax^2+bx+c</math> פריק (מעל הממשיים, כמובן). נסמן <math>ax^2+bx+c=a(x-\alpha)(x-\beta)</math> . | ||
| + | |||
| + | הצבת אוילר: נציב <math>\sqrt{ax^2+bx+c}=u(x-\alpha)</math> (אפשר גם את השורש השני). נביע את <math>x</math> באמצעות <math>u</math> , ונוכל למצוא גם את <math>x</math> וגם את <math>\sqrt{ax^2+bx+c}</math> . | ||
| + | |||
| + | ====דוגמא==== | ||
| + | <math>\int\frac{dx}{x\sqrt{x^2-7x+6}}</math> | ||
| + | |||
| + | |||
| + | נעזר בהצבת אוילר: נציב <math>\sqrt{x^2-7x+6}=u(x-1)</math> . | ||
| + | |||
| + | |||
| + | לכן <math>(x-1)(x-6)=u^2(x-1)^2</math> , כלומר <math>x-6=u^2(x-1)</math> , ומכאן <math>x=\frac{u^2-6}{u^2-1}</math> . | ||
| + | |||
| + | |||
| + | לכן <math>dx=\frac{2u(u^2-1)-2u(u^2-6)}{(u^2-1)^2}du=\frac{10u}{(1-u^2)^2}du</math> . | ||
| + | |||
| + | |||
| + | בנוסף, <math>\sqrt{x^2-7x+6}=u(x-1)=u\left(\frac{u^2-6}{u^2-1}-1\right)=-\frac{5u}{u^2-1}</math> | ||
| + | |||
| + | מקבלים: | ||
| + | |||
| + | <math>\int\frac{dx}{x\sqrt{x^2-7x+6}}=-\int\frac{1}{\frac{u^2-6}{u^2-1}\cdot\frac{5u}{u^2-1}}\cdot\frac{10u}{(1-u^2)^2}du=-2\int\frac{du}{u^2-6}</math> כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים. | ||
| + | |||
| + | ===אוילר 2 - פולינום יותר כללי=== | ||
| + | ישנן שתי אפשרויות: | ||
| + | # בהינתן <math>a>0</math> , נציב <math>\sqrt{ax^2+bx+c}=\sqrt{a}x+u</math> . | ||
| + | # בהינתן <math>c>0</math> , נציב <math>\sqrt{ax^2+bx+c}=xu+\sqrt c</math> . | ||
| + | |||
| + | נביע את <math>x</math> באמצעות <math>u</math> , ונוכל למצוא את <math>dx</math> ואת <math>\sqrt{ax^2+bx+c}</math> . | ||
| + | |||
| + | ====דוגמא==== | ||
| + | <math>\int\frac{dx}{\sqrt{x^2-7x+6}}</math> | ||
| + | |||
| + | ניעזר בהצבת אוילר (האופציה הראשונה): נציב <math>\sqrt{x^2-7x+6}=x+u</math> . | ||
| + | |||
| + | |||
| + | נעלה בריבוע ונקבל <math>x^2-7x+6=x^2+2xu+u^2</math> , כלומר <math>x=\frac{6-u^2}{2u+7}</math> . | ||
| + | |||
| + | |||
| + | לכן <math>dx=\frac{-2u(2u+7)-2(6-u^2)}{(2u+7)^2}du=-2\cdot\frac{u^2+7u+6}{(2u+7)^2}du</math> , | ||
| + | |||
| + | |||
| + | וכן <math>\sqrt{x^2-7x+6}=x+u=\frac{6-u^2}{2u+7}+u=\frac{6-u^2+2u^2+7u}{2u+7}=\frac{u^2+7u+6}{2u+7}</math> . | ||
| + | |||
| + | מקבלים: | ||
| + | |||
| + | <math>\int\frac{dx}{\sqrt{x^2-7x+6}}=-\int\frac{1}{\frac{u^2+7u+6}{2u+7}}\cdot2\cdot\frac{u^2+7u+6}{(2u+7)^2}du=-\int\frac{2}{2u+7}du=-\ln(|2u+7|)+C=-\ln\left(\left|\sqrt{x^2-7x+6}-x\right|\right)+C</math> | ||
| + | |||
| + | |||
| + | [[מדיה:09Infi2Universal.pdf|הרחבה]] | ||
| + | |||
| + | ==סיכום== | ||
| + | '''[[מדיה:אינטגרלים לא-מסוימים.pdf|דף מסכם]]''' | ||
גרסה אחרונה מ־13:52, 15 במרץ 2019
בדף זה יוצגו מספר שיטות אינטגרציה הניתנות לשימוש. בסיום הדף מצורף קובץ המסכם את מה שנכתב כאן.
תוכן עניינים
אינטגרציה מיידית
אינטגרל מיידי הוא אינטגרל על פונקציה שאנחנו יודעים מי הקדומה שלה.
לדוגמא: 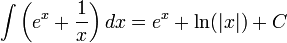
אינטגרציה בחלקים
לפי נוסחת הגזירה של מכפלת פונקציות (נוסחת לייבניץ), אנו מקבלים:
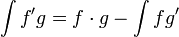 (ניתן לוודא על ידי גזירה).
(ניתן לוודא על ידי גזירה).
דוגמא
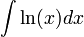
לפי השיטה, נסמן 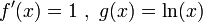 .
.
לכן נקבל 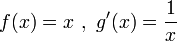 .
.
לפי נוסחת אינטגרציה בחלקים, נקבל:
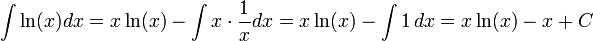
אינטגרציה בהצבה
לפי כלל השרשרת, אנו מקבלים:
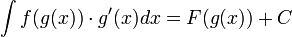 (ניתן לוודא על-ידי גזירה).
(ניתן לוודא על-ידי גזירה).
דוגמא
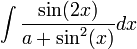 כאשר
כאשר 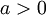 .
.
נבצע הצבהעיבוד הנוסחה נכשל (שגיאת לקסינג): u=\sin^2(x)\
ולכן עיבוד הנוסחה נכשל (שגיאת לקסינג): du=2\sin(x)\cos(x)dx=\sin(2x)dx\
מקבלים:
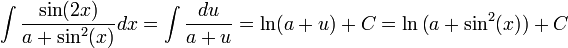 (נזכור כי
(נזכור כי 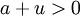 , לכן אין צורך בערך מוחלט).
, לכן אין צורך בערך מוחלט).
פונקציה רציונאלית
על מנת לחשב אינטגרל על פונקציה רציונאלית 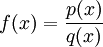 (כאשר
(כאשר 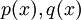 פולינומים), עלינו לעקוב אחרי השלבים הבאים:
פולינומים), עלינו לעקוב אחרי השלבים הבאים:
- אם דרגת המונה גדולה מדרגת המכנה, נבצע חילוק פולינומים.
- נבצע פירוק לשברים חלקיים.
- נחשב את האינטגרל של כל שבר חלקי.
ניתן לקרוא כאן את האלגוריתם המלא.
הצבות אוניברסאליות
הצבות אוניברסאליות הוא כינוי כללי להצבות המעבירות פונקציות ממשפחה מסוימת לצורה של פונקציה רציונאלית אותה אנחנו יודעים לפתור. שימו לב שכיון ופתרון פונקציה רציונאלית דורש פירוק פולינומים, לעתים המעבר לפונקציה רציונאלית לא יקדם אותנו לקראת פתרון הבעיה.
הצבות אוניברסאליות ידועות ניתן למצוא בקובץ הבא: (עד אשר מישהו יקליד אותו אל תוך הויקי...)
ההצבה הטריגונומטרית האוניברסלית
בהינתן פונקציה אשר משולבות בה פונקציות טריגונומטריות (ועדיף שהיא תהיה מנה של חיבור וכפל שלהן), אזי נציב 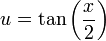 .
.
נזכור כי 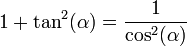 , ונקבל
, ונקבל 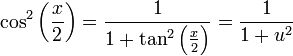 .
.
נקבל בנוסף 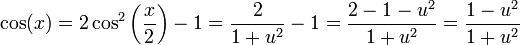 .
.
לכן:
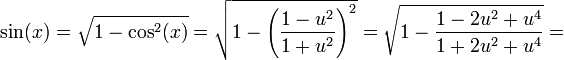
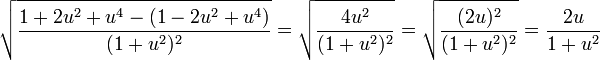
ובדרך אחרת:
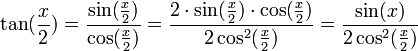
ולכן מתקיים
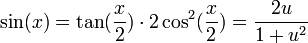
כמו כן, 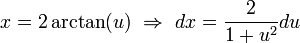 .
.
לסיכום,
דוגמא
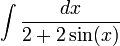
נעזר בהצבה הטריגונומטרית האוניברסלית. נציב 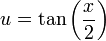 . נקבל:
. נקבל:
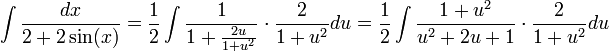
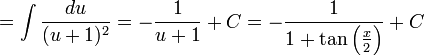
הצבות אוילר
הצבות אוילר מתייחסות למקרה של פונקציה "רציונאלית" אשר הרכיבים בה הם  ו-
ו- 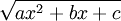 .
.
אוילר 1 - הפולינום פריק
נניח כי הפולינום 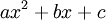 פריק (מעל הממשיים, כמובן). נסמן
פריק (מעל הממשיים, כמובן). נסמן 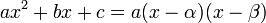 .
.
הצבת אוילר: נציב 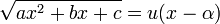 (אפשר גם את השורש השני). נביע את
(אפשר גם את השורש השני). נביע את  באמצעות
באמצעות 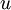 , ונוכל למצוא גם את
, ונוכל למצוא גם את  וגם את
וגם את 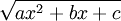 .
.
דוגמא
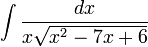
נעזר בהצבת אוילר: נציב 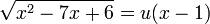 .
.
לכן 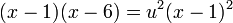 , כלומר
, כלומר 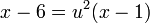 , ומכאן
, ומכאן 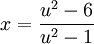 .
.
לכן 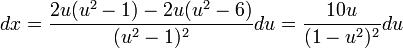 .
.
בנוסף, 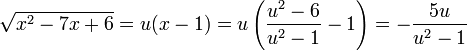
מקבלים:
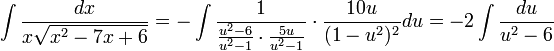 כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים.
כאשר האינטגרל האחרון ניתן לפתרון באמצעות פירוק לשברים חלקיים.
אוילר 2 - פולינום יותר כללי
ישנן שתי אפשרויות:
- בהינתן
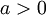 , נציב
, נציב 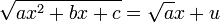 .
. - בהינתן
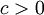 , נציב
, נציב 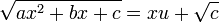 .
.
נביע את  באמצעות
באמצעות 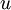 , ונוכל למצוא את
, ונוכל למצוא את 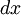 ואת
ואת 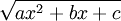 .
.
דוגמא
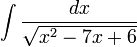
ניעזר בהצבת אוילר (האופציה הראשונה): נציב 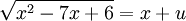 .
.
נעלה בריבוע ונקבל 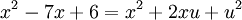 , כלומר
, כלומר 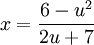 .
.
לכן 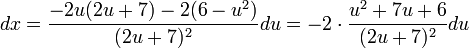 ,
,
וכן 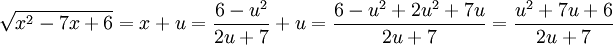 .
.
מקבלים: