שיטות אינטגרציה

בדף זה יוצגו מספר שיטות אינטגרציה הניתנות לשימוש.

אינטגרציה "רגילה"

הכוונה היא לבצע את האינטגרל לפי חוקי הגזירה. לדוגמה,
$\int \left(e^x+\frac{1}{x} \right )dx=e^x+ln\left | x \right |+c$.

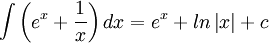השלמה לריבוע

כאשר נקבל פונקציה רציונאלית שבמונה שלה יש מספר ובמכנה שלה פולינום ממעלה שנייה, ניתן להשלים את הפולינום לריבוע ולהיעזר ב-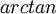$arctan$.

דוגמה

$\int\frac{1}{x^2+x+1\frac{1}{4}}dx$

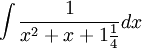
ניעזר בהשלמה לריבוע של המכנה. נקבל:

$\int\frac{1}{x^2+x+1\frac{1}{4}}dx=\int\frac{1}{\left (x+\frac{1}{2} \right )^2+1}dx=arctan\left (x+\frac{1}{2} \right )+c$

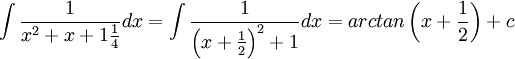
אינטגרציה בחלקים

לפי נוסחת הגזירה של מכפלת פונקציות (נוסחת לייבניץ), אנו מקבלים:
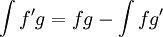$\int{f'g}=fg-\int{fg'}$ (ניתן לוודא על ידי גזירה).

דוגמה

נחפש את 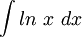$\int ln\ x \ dx$.

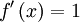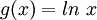לפי השיטה, נסמן $f'\left (x \right )=1$, $g(x)=ln\ x$.

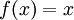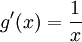לכן נקבל $f(x)=x$, $g'(x)=\frac{1}{x}$.

לפי נוסחת אינטגרציה בחלקים, נקבל:

$\int ln\ x \ dx=x\cdot ln\ x-\int x\cdot \frac{1}{x}\ dx=x\cdot ln\ x-\int 1\ dx=x\cdot ln\ x-x+c$.

הרחבה

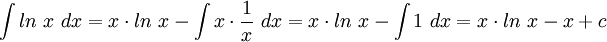הרחבה

אינטגרציה בהצבה

לפי כלל השרשרת, אנו מקבלים:
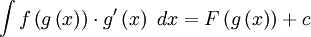$\int f\left (g\left(x \right ) \right )\cdot g'\left (x \right )\ dx=F\left (g\left(x \right ) \right )+c$ (ניתן לוודא על ידי גזירה).

דוגמה

נחפש את 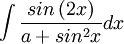$\int \frac{sin\left(2x \right )}{a+sin^2 x}dx$ כאשר $a>0$.

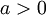נבצע הצבה: 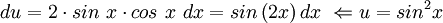$du=2\cdot sin\ x\cdot cos\ x\ dx=sin\left(2x \right )dx \ \Leftarrow u=sin^2 x$. מקבלים:

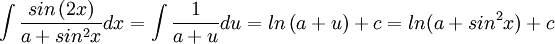$\int \frac{sin\left(2x \right )}{a+sin^2 x}dx=\int \frac{1}{a+u}du=ln\left ( a+u \right )+c=ln(a+sin^2 x)+c$ (נזכור כי 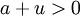$a+u>0$, לכן אין צורך בערך מוחלט).

הרחבה

הרחבה

ההצבה הטריגונומטרית האוניברסלית

בהינתן פונקציה אשר משולבות בה פונקציות טריגונומטריות (ועדיף שהיא תהיה מנה של חיבור וכפל שלהן), אזי נציב 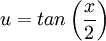$u=tan\left (\frac{x}{2}\right )$.

נזכור כי 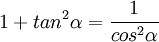$1+tan^2\alpha=\frac{1}{cos^2 \alpha}$, ונקבל $cos^2 \left ( \frac{x}{2} \right )=\frac{1}{1+tan^2\left ( \frac{x}{2} \right )}=\frac{1}{1+u^2}$.

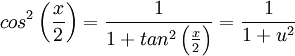נקבל בנוסף 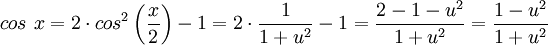$cos\ x=2\cdot cos^2\left ( \frac{x}{2} \right )-1=2\cdot\frac{1}{1+u^2}-1=\frac{2-1-u^2}{1+u^2}=\frac{1-u^2}{1+u^2}$.

לכן 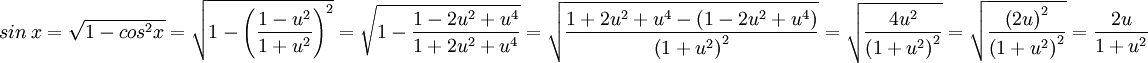$sin\ x=\sqrt{ 1-cos^2 x }=\sqrt{1-\left (\frac{1-u^2}{1+u^2} \right )^2}=\sqrt{1-\frac{1-2u^2+u^4}{1+2u^2+u^4}}=\sqrt{\frac{1+2u^2+u^4-\left (1-2u^2+u^4 \right )}{\left ( 1+u^2 \right )^2}}=\sqrt{\frac{4u^2}{\left ( 1+u^2 \right )^2}}=\sqrt{\frac{\left ( 2u \right )^2}{\left ( 1+u^2 \right )^2}}=\frac{2u}{1+u^2}$

כמו כן, 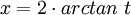$x=2\cdot arctan\ t$, ולכן $dx=\frac{2}{1+u^2} du$.

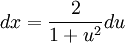דוגמה

$\int\frac{1}{2+2\cdot sin\ x}dx$

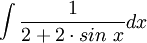
ניעזר בהצבה הטריגונומטרית האוניברסלית. נציב 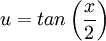$u=tan\left (\frac{x}{2}\right )$. נקבל:

$\int\frac{1}{2+2\cdot sin\ x}dx=\int\frac{1}{2+2\cdot \frac{2u}{1+u^2}}\cdot \frac{2}{1+u^2}du=\int\frac{1+u^2}{2+2u^2+4u}\cdot\frac{2}{1+u^2}du=\int\frac{1}{u^2+2u+1}du=\int\frac{1}{\left (u+1\right )^2}du=-\frac{1}{u+1}+c=-\frac{1}{1+tan\left (\frac{x}{2}\right )}+c$

הרחבה

הרחבה