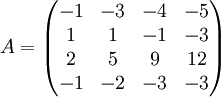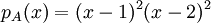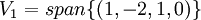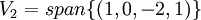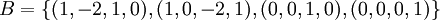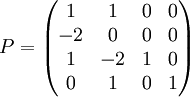שילוש מטריצה

הגדרה

מטריצה A נקראת ניתנת לשילוש אם קיימת מטריצה משולשית עליונה הדומה לה

משפט

מטריצה ריבועית ניתנת לשילוש אם ורק אם הפולינום האופייני שלה מתפרק לגורמים לינאריים

אלגוריתם לשילוש מטריצה

• ניקח את האיחוד של הבסיסים למרחבים העצמיים E ונשלים אותו לבסיס B

• נשים את וקטורי B בעמודות מטריצה P ונביט במטריצה $Q = P^{-1}AP$

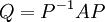
• נסמן 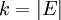$k=|E|$. נסמן ב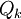$Q_k$ את המטריצה המתקבלת מ Q על ידי מחיקת k השורות הראשונות וk העמודות הראשונות.

• לפי אינדוקציה, ניתן לשלש את המטריצה 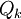$Q_k$ על ידי המטריצה $P_1$.

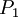• נסמן 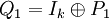$Q_1=I_k\oplus P_1$, כאשר 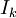$I_k$ הינה מטריצה היחידה מגודל k.

• סה"כ 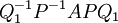$Q_1^{-1}P^{-1}APQ_1$ הינה מטריצה משולשית

דוגמאות

נשלש את המטריצה

$A=\begin{pmatrix}-1 & -3 & -4 & -5 \\ 1 & 1 & -1 & -3 \\ 2 & 5 & 9 & 12 \\ -1 & -2 & -3 & -3 \end{pmatrix}$

ראשית נמצא את הפולינום האופייני:

$p_A(x)=(x-1)^2(x-2)^2$

הוא מתפרק לגורמים לינאריים, לכן המטריצה ניתנת לשילוש. הע"ע הינם 1,2.

לאחר חישוב בסיסים למרחבים העצמיים אנו מקבלים:

$V_1=span\{(1,-2,1,0)\}$

$V_2=span\{(1,0,-2,1)\}$

נסמן $E = \{(1,-2,1,0),(1,0,-2,1)\}$

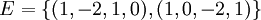
ונשלים אותו לבסיס

$B = \{(1,-2,1,0),(1,0,-2,1),(0,0,1,0),(0,0,0,1)\}$

נסמן

$P=\begin{pmatrix} 1 & 1 & 0 & 0 \\ -2 & 0 & 0 & 0 \\ 1 & -2 & 1 & 0\\ 0 & 1 & 0 & 1\end{pmatrix}$