הבדלים בין גרסאות בדף "תקציר שימושי מחשב, סמסטר ב תשעג, גיא בלשר"
(←קבלת מינימום) |
(←אלגוריתם אוקלידס) |
||
| שורה 318: | שורה 318: | ||
====אלגוריתם אוקלידס==== | ====אלגוריתם אוקלידס==== | ||
| + | |||
| + | אלגוריתם אוקלידס נועד למציאת מחלק משותף מקסימלי בין שני מספרים שלמים <math>m,n</math>. | ||
| + | |||
| + | '''האלגוריתם''' | ||
| + | |||
| + | נניח <math>m<n</math>. נגדיר: | ||
| + | <math>r_0=n</math> <BR> | ||
| + | <math>r_1=m</math><BR> | ||
| + | <math>r_0=q_1 r_1+r_2</math> כאשר <math>1\leq q_1 \leq r_0</math>, <math>0\leq r_2 <r_1</math><BR> | ||
| + | ובאינדוקציה <math>r_k=q_{k+1} r_{k+1}+r_{k+2}</math> <BR> | ||
| + | עד שנגיע ל־<math>r_N=0</math>. <BR> | ||
| + | בהכרח נעצור כי <math>r_{k+1}<r_k</math>. | ||
| + | |||
| + | לפי אלגוריתם זה, ה־gcd הינו <math>r_{N-1}</math>. | ||
| + | |||
| + | '''דוגמה''' | ||
| + | |||
| + | נבחר <math>r_0=30, r_1=12</math>. <BR> | ||
| + | <math>30=2\cdot 12+\underset{r_2}{\underbrace{6}}</math> <BR> | ||
| + | <math>12=2\cdot 6+\underset{r_3}{\underbrace{0}}</math><BR> | ||
| + | ולכן <math>gcd(30,12)=6</math> | ||
| + | |||
| + | '''הוכחת האלגוריתם''' | ||
| + | |||
| + | <math>r_{N-2}=q_{N-1} r_{N-1}+r_N=q_{N-1} r_{N-1}</math> <math>\Leftarrow</math> <math>r_{N-1}|r_{N-2}</math>. <BR> <BR> | ||
| + | <math>r_{N-3}=q_{N-2} r_{N-2}+r_{N-1}</math>. <BR> | ||
| + | <math>r_{N-1}|r_{N-2}</math> וגם <math>r_{N-1}|r_{N-1}</math> <math>\Leftarrow</math><math>r_{N-1}|r_{N-3}</math> <BR><BR> | ||
| + | <math>r_{N-4}=q_{N-3} r_{N-3}+r_{N-2}</math>. <BR> | ||
| + | <math>r_{N-1}|r_{N-2}</math> וגם <math>r_{N-1}|r_{N-3}</math> <math>\Leftarrow</math><math>r_{N-1}|r_{N-4}</math> <BR><BR <BR><BR> | ||
| + | באינדוקציה, נקבל <math>r_{N-1}|r_1</math> וגם <math>r_{N-1}|r_0</math>. | ||
| + | |||
| + | מדוע <math>r_{N-1}</math> הוא המחלק המשותף הגדול ביותר? נניח <math>r_k=gcd(m,n)</math>, אזי <math>r_{k-1}=q_{k} r_{k}+0</math>. | ||
| + | |||
| + | בהכרח נגיע למחלק המשותף המקסימלי מפני שבשלב ה־k־י, <math>r_{k-1}|gcd(m,n)</math> וגם <math>r_k|gcd(m,n)</math>, לכן <math>r_{k+1}|gcd(m,n)</math>. | ||
| + | |||
| + | '''תכנות''' | ||
| + | |||
| + | <div align="left"> | ||
| + | ;m=12 | ||
| + | ;n=30 | ||
| + | if n<m | ||
| + | ;r1=n | ||
| + | ;r0=m | ||
| + | else | ||
| + | ;r1=m | ||
| + | ;r0=n | ||
| + | end | ||
| + | while r1>0 | ||
| + | ;(r2=mod(r0,r1 | ||
| + | ;r0=r1 | ||
| + | ;r1=r2 | ||
| + | end | ||
| + | ;gcd=r0 | ||
| + | <div align="right"> | ||
| + | |||
| + | '''דוגמה''' | ||
| + | |||
| + | עבור <math>m=169, n=1482</math> | ||
| + | {| border="1" align="center" | ||
| + | ! <math>r_2</math> | ||
| + | ! <math>r_1</math> | ||
| + | ! <math>r_0</math> | ||
| + | |- | ||
| + | | | ||
| + | | 169 | ||
| + | | 1482 | ||
| + | |- | ||
| + | | 130 | ||
| + | | 130 | ||
| + | | 169 | ||
| + | |- | ||
| + | | 39 | ||
| + | | 39 | ||
| + | | 130 | ||
| + | |- | ||
| + | | 13 | ||
| + | | 13 | ||
| + | | 39 | ||
| + | |- | ||
| + | | 0 | ||
| + | | 0 | ||
| + | | 13 | ||
| + | |} | ||
| + | gcd(169,1482)=13 | ||
| + | |||
| + | |||
| + | עבור <math>m=441, n=42</math> | ||
| + | {| border="1" align="center" | ||
| + | ! <math>r_2</math> | ||
| + | ! <math>r_1</math> | ||
| + | ! <math>r_0</math> | ||
| + | |- | ||
| + | | | ||
| + | | 42 | ||
| + | | 441 | ||
| + | |- | ||
| + | | 21 | ||
| + | | 21 | ||
| + | | 42 | ||
| + | |- | ||
| + | | 0 | ||
| + | | 0 | ||
| + | | 21 | ||
| + | |} | ||
| + | gcd(42,441)=21 | ||
====פתרון מערכת משוואות - ניוטון-רפסון==== | ====פתרון מערכת משוואות - ניוטון-רפסון==== | ||
תהי <math>f(x)</math> פונקציה, צריך למצוא <math>x</math> כך ש־<math>f(x)=0</math>. | תהי <math>f(x)</math> פונקציה, צריך למצוא <math>x</math> כך ש־<math>f(x)=0</math>. | ||
גרסה מ־11:45, 19 ביוני 2013
תאריך עדכון אחרון: 19 ביוני 2013
תוכן עניינים
תוכנה 1: MATLAB
הערה: ב־MATLAB בסוף כך שורת הוראה יש להוסיף ; על מנת שלא תתבצע הדפסה, אך אם רוצים הדפסה אין להוסיף ; בסוף השורה.
עבודה בסיסית ב־MATLAB
משתנים
משתנה הוא סמל המסמן כמות, איבר של קבוצה, או ערך לוגי, העשויים להשתנות (מתוך ויקיפדיה).
השמה למשתנה - הכנסת ערך אליו. ב־MATLAB (דוגמות):
x=3
z=pi
w=4+5*i
פעולות בסיסיות עם משתנים (a,b מציינים מספרים):
| הפעולה | הסימן ב־MATLAB |
|---|---|
| חיבור | a+b |
| חיסור | a-b |
| כפל | a*b |
| חילוק | / |
| חזקה | a^b |
| לוגריתם טבעי (ln) | (log(a |
| שורש ריבועי | (sqrt(a |
| ערך שלם / רצפה | (floor(a |
| שארית חלוקה (רק עבור שלמים) | (mod(a,b |
להוספת הערה בסוף שורה כותבים את הסימן % ולאחריו את ההערה.
בחילוק שני מספרים שלמים, המנה היא (floor(x,y והשארית היא (mod(x,y.
משתנים קבועים: i,j - ה־i המרוכב, 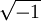 , pi - פאי.
, pi - פאי.
הדפסת ערך משתנה:
(disp(value
מטריצות
פעולות בסיסיות עם משתנים (A,B מציינים מטריצות):
| הפעולה | ההוראה ב־MATLAB |
|---|---|
הגדרת מטריצת אפסים בגודל 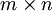
|
(A=zeros(m,n |
| איבר בשורה x ובעמודה y | (A(x,y |
| חיבור מטריצות | A+B |
| חיסור מטריצות | A-B |
| כפל במובן מטריצות | A*B |
| כפל איבר־איבר | A.*B |
| חילוק (כפל בהופכית) | A/B |
| חילוק איבר־איבר | A./B |
| מימדי מטריצה (וקטור) | (size(A |
| שחלוף (transpose) | 'A |
ועוד...
הערה 1: האינדקסים במטריצה מתחילים מ־1.
הערה 2: אם נעשתה פנייה לאיבר שאינו במערך והושם בו ערך, MATLAB ירחיב באופן אוטומטי את המערך, ובמקומות שנוספו יושמו אפסים.
מערכים: מטריצה מגודל nx1
פעולות בסיסיות עם מערכים (v מייצג וקטור, m,n,p מייצגים מספר כלשהו):
| הפעולה | ההוראה ב־MATLAB |
|---|---|
| אתחול (הצבת אפסים) | (v=zeros(n,1 |
| האיבר ה־n-י | (v(n |
| אורך הוקטור | (length(v |
| וקטור המכיל את המספרים הטבעיים עד n | v=1:n |
| וקטור המכיל את כל המספרים מ־m עד n בקפיצות p | v=m:p:n |
דוגמה: בכתיבה 1:5 יווצר הווקטור [5 4 3 2 1]. בכתיבה 1:2:5 יווצר הוקטור [5 3 1].
ניתן להגדיר וקטור גם באופן הבא: [w=[3 9 10 11 4 (במקום רווחים ניתן להשתמש בפסיקים). על מנת להגדיר מטריצה באופן דומה מוסיפים ; כדי לרדת שורה.
ניתן לקבל וקטור מאינדקסים מסוימים. למשל, עבור w שהוגדר,
[w(1:2:5)=w([1 3 5])=[3 10 4
פעולות בוליאניות
פעולות בוליאניות מחזירות 0 (שקר) או 1 (אמת). דוגמות (a,b מספרים):
| הפעולה | הסימון ב־MATLAB |
|---|---|
| האם שני ערכים שווים | a==b |
| קטן | ab |
| קטן שווה | a<=b |
| גדול שווה | a>=b |
| אינו שווה | =~ |
&& - וגם, || - או
תנאים
תנאי פשוט:
(תנאי) if
הוראות לביצוע
end
תנאי מורכב:
(תנאי) if
(הוראות לביצוע)
else
(הוראות לביצוע)
end
תנאי יותר מורכב:
(תנאי) if
(הוראות לביצוע)
elseif
(הוראות לביצוע)
else
(הוראות לביצוע)
end
לולאת for
לולאת for - ביצוע אותו רצף הוראות מספר ידוע מראש של פעמים.
תכנות:
(וקטור המכיל את ערכי i הדרושים)=for i
(הוראות לביצוע)
end
הערה: אמנם i הוא קבוע, אך ניתן להציב בו ערך. על מנת להחזירו להיות ה־i המרוכב, נכתוב את ההוראה clear i.
לולאת while
לולאת while - ביצוע אותו רצף הוראות מספר שאינו ידוע מראש של פעמים אך עם תנאי לעצירה.
תכנות:
(תנאי לעצירה, תנאי בוליאני) while
(הוראות לביצוע)
end
תרגילים
תרגיל 1 - עצרת
חשבו את 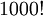 .
.
פתרון 1 - לולאת for:
;n=1 for i=2:1000 ;n=n*i end ;(disp(n
פתרון 2 - לולאת while:
;n=1 ;i=1 while i<=1000 ;n=n*i ;i=i+1 end ;(disp(n
תרגיל 2 - מספרים ראשוניים
צרו וקטור המכיל את כל המספרים הראשוניים מ־1 עד 1000
;כמה ראשוניים מצאנו % found=0
;וקטור עם המספרים הראשוניים % []=primes
for p=1:1000
;yesno=1
;k=2
while k<=sqrt(p) && yesno==1
if mod(p,k)==0
;yesno=0
end
;k=k+1
end
if yesno==1
;found=found+1
;primes(found)=p
end
end
תרגיל 3 - פירוק מספר שלם לגורמים ראשוניים
פרקו מספר שלם 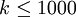 לגורמים ראשוניים (אפשר להשתמש בוקטור primes מהתרגיל הקודם).
לגורמים ראשוניים (אפשר להשתמש בוקטור primes מהתרגיל הקודם).
;k=252
while k>1
;i=2
while mod(k,primes(i))!~=0
;i=i+1
end
;((disp(primes(i
;(k=k/primes(i
end
יישומים מתמטיים
מחלק משותף גדול ביותר gcd
עבור 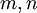 שלמים, המספר השלם הגדול ביותר המחלק גם את
שלמים, המספר השלם הגדול ביותר המחלק גם את 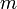 וגם את
וגם את  ייקרא המחלק המשותף הגדול ביותר ויסומן
ייקרא המחלק המשותף הגדול ביותר ויסומן 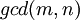 .
.
;m=12
;n=30
if n<m
;t=m
;m=n
;n=t
end
for i=1:m
if mod(m,i)==0 && mod(n,i)=0
;gcd=i
end
end
;(disp(gcd
קבלת מינימום
ישנן שלוש דרכים לקבל את המספר המינימלי מבין 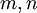 .
.
דרך ראשונה - ([min([m,n
דרך שנייה - תנאי
דרך שלישית - 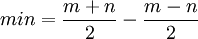
אלגוריתם אוקלידס
אלגוריתם אוקלידס נועד למציאת מחלק משותף מקסימלי בין שני מספרים שלמים 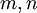 .
.
האלגוריתם
נניח 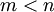 . נגדיר:
. נגדיר:
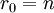
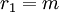
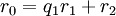 כאשר
כאשר 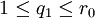 ,
, 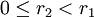
ובאינדוקציה 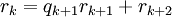
עד שנגיע ל־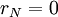 .
.
בהכרח נעצור כי 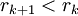 .
.
לפי אלגוריתם זה, ה־gcd הינו 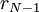 .
.
דוגמה
נבחר 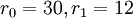 .
.
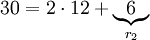
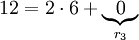
ולכן 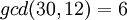
הוכחת האלגוריתם
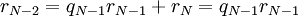
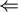
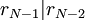 .
.
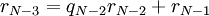 .
.
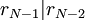 וגם
וגם 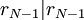
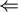
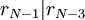
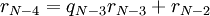 .
.
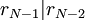 וגם
וגם 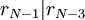
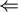
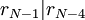
<BR
באינדוקציה, נקבל 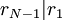 וגם
וגם 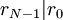 .
.
מדוע 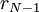 הוא המחלק המשותף הגדול ביותר? נניח
הוא המחלק המשותף הגדול ביותר? נניח 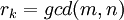 , אזי
, אזי 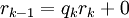 .
.
בהכרח נגיע למחלק המשותף המקסימלי מפני שבשלב ה־k־י, 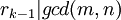 וגם
וגם 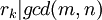 , לכן
, לכן 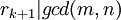 .
.
תכנות
;m=12 ;n=30 if n<m ;r1=n ;r0=m else ;r1=m ;r0=n end while r1>0 ;(r2=mod(r0,r1 ;r0=r1 ;r1=r2 end ;gcd=r0
דוגמה
עבור 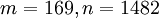
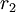
|
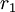
|
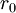
|
|---|---|---|
| 169 | 1482 | |
| 130 | 130 | 169 |
| 39 | 39 | 130 |
| 13 | 13 | 39 |
| 0 | 0 | 13 |
gcd(169,1482)=13
עבור 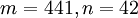
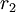
|
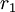
|
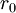
|
|---|---|---|
| 42 | 441 | |
| 21 | 21 | 42 |
| 0 | 0 | 21 |
gcd(42,441)=21
פתרון מערכת משוואות - ניוטון-רפסון
תהי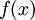 פונקציה, צריך למצוא
פונקציה, צריך למצוא  כך ש־
כך ש־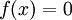 .
.