הבדלים בין גרסאות בדף "תרגול 14 תשעח"
(יצירת דף עם התוכן "=== תרגיל === הוכיחו כי <math>|P(\mathbb{N})|=|P(\mathbb{N})-\{\emptyset\}|</math> ==== פתרון ==== נגדיר פונקציה <math>f:P(\mathbb...") |
|||
| שורה 1: | שורה 1: | ||
| + | חזרה ל[[83-116, בדידה 1 להנדסה, מערכי תרגול|דף מערכי התרגול]]. | ||
| + | |||
| + | =עוצמות= | ||
| + | |||
| + | '''הגדרה.''' יהיו <math>A,B</math> שתי קבוצות. אזי: | ||
| + | *אם קיימת <math>f:A\to B </math> חח"ע ועל אז אומרים של-<math>A</math> ול-<math>B</math> '''יש אותה עוצמה'''. סימון <math>|A|=|B|</math>. | ||
| + | *אם קיימת <math>f:A\to B </math> חח"ע אז אומרים כי העוצמה של <math>A</math> קטנה או שווה לזו של <math>B</math>. סימון <math>|A|\leq|B|</math>. | ||
| + | * אם <math>|A|\leq|B|</math> וגם <math>|A|\not=|B|</math> אזי אומרים כי העוצמה של <math>A</math> קטנה ממש מהעוצמה של <math>B</math>. סימון <math>|A|<|B|</math>. | ||
| + | |||
| + | הערה: בעזרת אקסיומת הבחירה מוכיחים כי אם קיימת <math>f:A\to B </math> על אזי <math>|B|\leq |A|</math>. | ||
| + | |||
=== תרגיל === | === תרגיל === | ||
| − | הוכיחו כי <math>|P(\mathbb{N})|=|P(\mathbb{N})-\{\ | + | הוכיחו כי <math>|P(\mathbb{N})|=|P(\mathbb{N})-\{\varnothing\}|</math>. |
==== פתרון ==== | ==== פתרון ==== | ||
| − | נגדיר פונקציה <math>f:P(\mathbb{N})\to P(\mathbb{N})-\{\ | + | נגדיר פונקציה <math>f:P(\mathbb{N})\to P(\mathbb{N})-\{\varnothing\} </math> ע"י <math>\{n\}\mapsto \{n+1\},\varnothing \mapsto \{1\}</math> וכל <math>B</math> שאינה נקודון ואינה הקבוצה הריקה נשלח לעצמה. |
===תרגיל === | ===תרגיל === | ||
| − | הוכיחו כי <math>|A\times A| = |A^{\{1,2\}}|</math> | + | הוכיחו כי <math>|A\times A| = |A^{\{1,2\}}|</math>. |
פתרון: הפונקציה <math>F:A^{\{1,2\}}\to A\times A</math> המוגדרת <math>f\mapsto (f(1),f(2))</math> הפיכה. | פתרון: הפונקציה <math>F:A^{\{1,2\}}\to A\times A</math> המוגדרת <math>f\mapsto (f(1),f(2))</math> הפיכה. | ||
| − | ===משפט (קנטור- שרדר-ברנשטיין)=== | + | ===משפט (קנטור-שרדר-ברנשטיין)=== |
| − | אם <math>|B|\leq|A|</math> וגם <math>|A|\leq|B|</math> אז <math>|B|=|A|</math> | + | אם <math>|B|\leq|A|</math> וגם <math>|A|\leq|B|</math> אז <math>|B|=|A|</math>. |
| + | |||
| + | בהמשך נקצר לק.ש.ב. | ||
===תרגיל=== | ===תרגיל=== | ||
| − | הוכיחו: <math>|\mathbb{Q}\cap [0,1]|=\aleph_0</math> | + | הוכיחו: <math>|\mathbb{Q}\cap [0,1]|=\aleph_0</math>. |
====פתרון==== | ====פתרון==== | ||
| − | לפי ק.ש.ב. כי | + | לפי ק.ש.ב. כי הקבוצה מוכלת ברציונליים ומכילה <math>\aleph_0</math> שברים מהצורה <math>\frac{1}{n}</math>. |
| − | + | ||
===תרגיל=== | ===תרגיל=== | ||
| − | + | הוכיחו כי עוצמת כל הקבוצות הבאות שווה - כל קטעים מהצורה <math>[a,b],(a,b),[a,b),(a,b]</math> כאשר <math>a<b</math> ממשיים. | |
====פתרון==== | ====פתרון==== | ||
| שורה 29: | שורה 41: | ||
נראה שכולם שווי עוצמה לקטע <math>(0,1)</math>. | נראה שכולם שווי עוצמה לקטע <math>(0,1)</math>. | ||
| − | ראשית נגדיר <math>f:(0,1)\rightarrow (a,b)</math> ע"י | + | ראשית נגדיר <math>f:(0,1)\rightarrow (a,b)</math> ע"י <math>f(x)=a+(b-a)x</math> חח"ע ועל. השאר עם ק.ש.ב. |
| − | + | ||
| − | + | ||
| − | + | טענה: הקטע <math>(\frac{-\pi}{2},\frac{\pi}{2})</math> בעל עוצמה שווה ל-<math>\mathbb{R}</math>. | |
| + | הוכחת הטענה: הפונקציה <math>\tan:(\frac{-\pi}{2},\frac{\pi}{2})\to \mathbb{R}</math> הפיכה בתחום הזה ולכן חח"ע ועל. | ||
===תרגיל === | ===תרגיל === | ||
| − | תהא A קבוצה. | + | תהא <math>A</math> קבוצה. הוכיחו כי <math>|A|\leq |P(A)|</math>. |
| − | פתרון: נגדיר את הפונקציה <math>f:A|\to P(A)</math> ע"י <math>a \mapsto \{a\}</math> | + | פתרון: נגדיר את הפונקציה <math>f:A|\to P(A)</math> ע"י <math>a \mapsto \{a\}</math> והיא חח"ע. |
| − | תהא A קבוצה. | + | תהא <math>A</math> קבוצה. הוכיחו כי <math>|A|\neq |P(A)|</math>. |
| − | פתרון: נניח בשלילה כי <math>|A|= |P(A)|</math> אזי קיימת <math>f: A\to P(A)</math> הפיכה, בפרט על. נגדיר <math>X=\{a\in A: a\notin f(a)\}</math>. זוהי תת קבוצה של A ולכן, מכיוון ש f על, קיים <math>x\in A</math> כך ש <math>f(x)=X</math>. האם <math>x\in X</math>? אם לא, לפי הגדרת X נקבל כי <math>x\notin f(x)= | + | פתרון: נניח בשלילה כי <math>|A|= |P(A)|</math> אזי קיימת <math>f: A\to P(A)</math> הפיכה, בפרט על. נגדיר <math>X=\{a\in A: a\notin f(a)\}</math>. זוהי תת קבוצה של <math>A</math> ולכן, מכיוון ש-<math>f</math> על, קיים <math>x\in A</math> כך ש-<math>f(x)=X</math>. האם <math>x\in X</math>? אם לא, לפי הגדרת <math>X</math> נקבל כי <math>x\notin f(x)=X</math>, סתירה. אם כן אז <math>x\in X=f(x)</math> אבל לפי הגדרת <math>X</math> מתקיים <math>x\notin f(x)</math> סתירה. מש"ל. |
גרסה מ־22:39, 20 בינואר 2018
חזרה לדף מערכי התרגול.
תוכן עניינים
עוצמות
הגדרה. יהיו 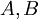 שתי קבוצות. אזי:
שתי קבוצות. אזי:
- אם קיימת
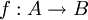 חח"ע ועל אז אומרים של-
חח"ע ועל אז אומרים של- ול-
ול- יש אותה עוצמה. סימון
יש אותה עוצמה. סימון 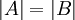 .
. - אם קיימת
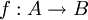 חח"ע אז אומרים כי העוצמה של
חח"ע אז אומרים כי העוצמה של  קטנה או שווה לזו של
קטנה או שווה לזו של  . סימון
. סימון 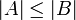 .
. - אם
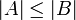 וגם
וגם 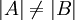 אזי אומרים כי העוצמה של
אזי אומרים כי העוצמה של  קטנה ממש מהעוצמה של
קטנה ממש מהעוצמה של  . סימון
. סימון 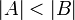 .
.
הערה: בעזרת אקסיומת הבחירה מוכיחים כי אם קיימת 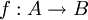 על אזי
על אזי 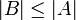 .
.
תרגיל
הוכיחו כי 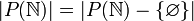 .
.
פתרון
נגדיר פונקציה 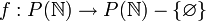 ע"י
ע"י 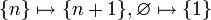 וכל
וכל  שאינה נקודון ואינה הקבוצה הריקה נשלח לעצמה.
שאינה נקודון ואינה הקבוצה הריקה נשלח לעצמה.
תרגיל
הוכיחו כי 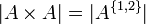 .
.
פתרון: הפונקציה 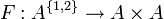 המוגדרת
המוגדרת 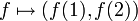 הפיכה.
הפיכה.
משפט (קנטור-שרדר-ברנשטיין)
אם 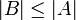 וגם
וגם 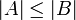 אז
אז 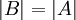 .
.
בהמשך נקצר לק.ש.ב.
תרגיל
הוכיחו: ![|\mathbb{Q}\cap [0,1]|=\aleph_0](/images/math/c/c/d/ccdd5439ef1126a8fbc14c6fa6003f37.png) .
.
פתרון
לפי ק.ש.ב. כי הקבוצה מוכלת ברציונליים ומכילה 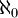 שברים מהצורה
שברים מהצורה  .
.
תרגיל
הוכיחו כי עוצמת כל הקבוצות הבאות שווה - כל קטעים מהצורה ![[a,b],(a,b),[a,b),(a,b]](/images/math/f/a/2/fa230f7985742fb91303cd7422bb5db4.png) כאשר
כאשר 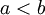 ממשיים.
ממשיים.
פתרון
נראה שכולם שווי עוצמה לקטע 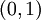 .
.
ראשית נגדיר 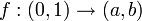 ע"י
ע"י 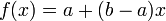 חח"ע ועל. השאר עם ק.ש.ב.
חח"ע ועל. השאר עם ק.ש.ב.
טענה: הקטע 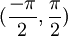 בעל עוצמה שווה ל-
בעל עוצמה שווה ל-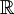 .
.
הוכחת הטענה: הפונקציה 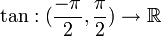 הפיכה בתחום הזה ולכן חח"ע ועל.
הפיכה בתחום הזה ולכן חח"ע ועל.
תרגיל
תהא  קבוצה. הוכיחו כי
קבוצה. הוכיחו כי 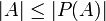 .
.
פתרון: נגדיר את הפונקציה 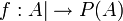 ע"י
ע"י 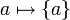 והיא חח"ע.
והיא חח"ע.
תהא  קבוצה. הוכיחו כי
קבוצה. הוכיחו כי 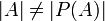 .
.
פתרון: נניח בשלילה כי 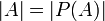 אזי קיימת
אזי קיימת 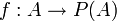 הפיכה, בפרט על. נגדיר
הפיכה, בפרט על. נגדיר 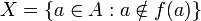 . זוהי תת קבוצה של
. זוהי תת קבוצה של  ולכן, מכיוון ש-
ולכן, מכיוון ש- על, קיים
על, קיים 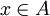 כך ש-
כך ש-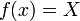 . האם
. האם 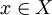 ? אם לא, לפי הגדרת
? אם לא, לפי הגדרת 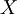 נקבל כי
נקבל כי 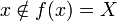 , סתירה. אם כן אז
, סתירה. אם כן אז 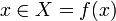 אבל לפי הגדרת
אבל לפי הגדרת 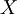 מתקיים
מתקיים 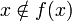 סתירה. מש"ל.
סתירה. מש"ל.