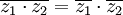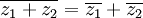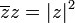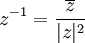הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/1"
(←משפט דמואבר) |
(←דירוג גאוס) |
||
| שורה 187: | שורה 187: | ||
===דירוג גאוס === | ===דירוג גאוס === | ||
| − | איבר '''מוביל/פותח/ציר''' הינו האיבר הראשון בשורה ששונה מאפס (משמאל לימין). מטריצה נקראת '''מדורגת''' אם מתחת לכל איבר מוביל שלה יש אפסים בלבד וכל איבר מוביל נמצא מימין לאיברים המובילים הקודמים. מטריצה נקראת '''מדורגת קנונית''' אם היא מדורגת, ובנוסף יש אפסים מעל לכל איבר מוביל והאיברים המובילים חייבים להיות שווים למספר אחד. | + | איבר '''מוביל/פותח/ציר''' הינו האיבר הראשון בשורה ששונה מאפס (משמאל לימין). מטריצה נקראת '''מדורגת''' אם מתחת לכל איבר מוביל שלה יש אפסים בלבד וכל איבר מוביל נמצא מימין לאיברים המובילים הקודמים. בנוסף, יש את הדרישה כי שורות אפסים (אם קיימות) נמצאות בסוף. מטריצה נקראת '''מדורגת קנונית''' אם היא מדורגת, ובנוסף יש אפסים '''מעל''' לכל איבר מוביל והאיברים המובילים חייבים להיות שווים למספר אחד. |
הערה: לכל מטריצה '''קיימת''' צורה קנונית '''יחידה'''. | הערה: לכל מטריצה '''קיימת''' צורה קנונית '''יחידה'''. | ||
כעת נלמד אלגוריתם המאפשר לנו לפתור מערכת משוואות לינארית באמצעות הצורה המטריצית שלה (בפרט, נדרג את המטריצה לצורתה הקנונית). תהליך זה נקרא '''[[מדיה: 10Linear1Gauss.pdf|אלגוריתם לדירוג גאוס]]'''. | כעת נלמד אלגוריתם המאפשר לנו לפתור מערכת משוואות לינארית באמצעות הצורה המטריצית שלה (בפרט, נדרג את המטריצה לצורתה הקנונית). תהליך זה נקרא '''[[מדיה: 10Linear1Gauss.pdf|אלגוריתם לדירוג גאוס]]'''. | ||
| − | |||
===תרגיל 1.5 סעיף ב'=== | ===תרגיל 1.5 סעיף ב'=== | ||
גרסה מ־15:09, 5 ביולי 2015
תוכן עניינים
שיעור ראשון
שדות
הגדרה: שדה.
תרגיל 1.3 סעיף ג'
יהי שדה 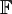 . הוכח שניתן לגזור מתכונות השדה את הטענה הבאה:
. הוכח שניתן לגזור מתכונות השדה את הטענה הבאה: 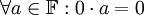 , כאשר 0 הינו הסימון לאיבר הנייטרלי החיבורי.
, כאשר 0 הינו הסימון לאיבר הנייטרלי החיבורי.
פתרון
ראשית נשים לב שלפי הנתונים ניתן להניח שאקסיומות השדה מתקיימות.
יהא 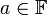 . צריך להוכיח כי
. צריך להוכיח כי 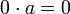
לפי תכונה (4) [ניטרליות 0 לחיבור] מתקיים ש 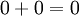
לכן 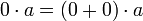
לפי תכונה (7) [פילוג] מתקיים בנוסף ש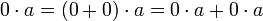 (השתמשנו בעצם בתכונה (7) לאחר שהפעלנו עליה את תכונה (2))
(השתמשנו בעצם בתכונה (7) לאחר שהפעלנו עליה את תכונה (2))
לפי תכונה (5) [קיום נגדי] לאיבר 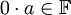 קיים איבר נגדי. נחבר אותו לשני צידי המשוואה לקבל
קיים איבר נגדי. נחבר אותו לשני צידי המשוואה לקבל 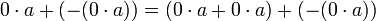
לפי תכונה (3) [קיבוציות] ניתן להחליף את סדר הסוגריים מימין ולקבל
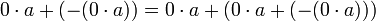
עוד לפי תכונה (5) [תכונת הנגדי] יחד עם תכונה (4) [נטרליות 0 לחיבור] מתקיים ש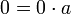 בדיוק כפי שרצינו להוכיח.
בדיוק כפי שרצינו להוכיח.
תרגיל 1.3 סעיף ו'
יהי שדה 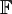 . הוכח שניתן לגזור מתכונות השדה את הטענה הבאה:
. הוכח שניתן לגזור מתכונות השדה את הטענה הבאה: 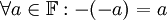 . (כלומר, הנגדי של הנגדי הוא האיבר עצמו)
. (כלומר, הנגדי של הנגדי הוא האיבר עצמו)
פתרון
יהא a בשדה צריך להוכיח כי 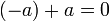 [זה הגדרת נגדי].
[זה הגדרת נגדי].
כיוון החיבור חילופי נקבל כי 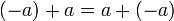 . כיוון ש
. כיוון ש 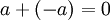 לפי הגדרת נגדי של a, סיימנו.
לפי הגדרת נגדי של a, סיימנו.
תרגיל 1.3 סעיף ז'
יהי שדה 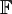 . הוכח שניתן לגזור מתכונות השדה את הטענה הבאה:
. הוכח שניתן לגזור מתכונות השדה את הטענה הבאה: 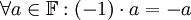 . (כלומר הנגדי של האיבר הנייטרלי הכפלי כפול a הינו הנגדי של a)
. (כלומר הנגדי של האיבר הנייטרלי הכפלי כפול a הינו הנגדי של a)
פתרון
מתוך תכונות (7),(5) וסעיף ג' שהוכחנו לעיל, 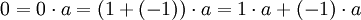
לפי תכונה (4) קיבלנו 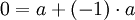
נוסיף לשני האגפים את הנגדי של a ונקבל 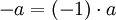 כפי שרצינו.
כפי שרצינו.
תרגיל 2.3 סעיף א'
יש להוכיח שקבוצת הטבעיים 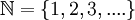 אינה שדה.
אינה שדה.
פתרון
אין איבר נייטרלי לחיבור: 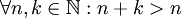 ואילו האיבר הנייטרלי היה צריך לקיים
ואילו האיבר הנייטרלי היה צריך לקיים 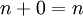 .
.
תרגיל 2.3 סעיף ג'
הגדרה: נגדיר את הקבוצה הבאה: 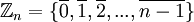 .
.
עובדה: עבור n=p ראשוני הקבוצה 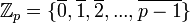 הינה שדה ביחס לחיבור וכפל מודלו p. הניטרלי לחיבור הוא 0 והנטרלי לכפל הוא 1. למשל
הינה שדה ביחס לחיבור וכפל מודלו p. הניטרלי לחיבור הוא 0 והנטרלי לכפל הוא 1. למשל 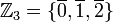
תרגיל: הוכיחו כי ש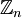 אינו שדה כאשר n מספר פריק (כלומר קיימים טבעיים כך ש n=mk)
ביחס לפעולות החיבור והכפל מודולו n.
אינו שדה כאשר n מספר פריק (כלומר קיימים טבעיים כך ש n=mk)
ביחס לפעולות החיבור והכפל מודולו n.
פתרון
לפי הנתונים קיימים 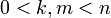 כך ש
כך ש 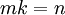 . לפיכך, לפי ההגדרה,
. לפיכך, לפי ההגדרה,
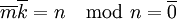 .
.
לו היה זה שדה, היו קיים הופכי ל m. אם היינו כופלים אותו בשני האגפים היינו מקבלים:
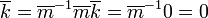
ולכן 0=k בסתירה להגדרת k.
תרגיל 2.6
הסבר מדוע 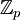 אינו תת שדה של
אינו תת שדה של 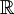
פתרון
תת שדה הינו תת קבוצה של איברים, תחת אותן פעולות כמו בשדה. לכן 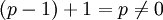 ולכן אין סגירות לחיבור וזה אינו תת שדה.
ולכן אין סגירות לחיבור וזה אינו תת שדה.
מרוכבים
נגדיר מרוכבים, נראה שרוב תכונות השדה הן טריוויאליות פרט לקיום ההופכי וגם זה ניתן להוכחה.
תרגיל 3.2
אם נשנה את פעולת כפל המרוכבים לפעולה הבאה: 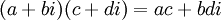 , האם קבוצת המרוכבים תשאר שדה?
, האם קבוצת המרוכבים תשאר שדה?
פתרון
לא. ניקח 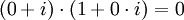 כלומר יש לנו איברים שונים מאפס שמכפלתם הינה אפס. בדומה לתרגיל קודם, אם נכפול בהופכיים שלהם נקבל 1=0 בסתירה.
כלומר יש לנו איברים שונים מאפס שמכפלתם הינה אפס. בדומה לתרגיל קודם, אם נכפול בהופכיים שלהם נקבל 1=0 בסתירה.
תרגיל 3.4
הצג את הביטוי הבא בצורה 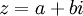 וציין מהם
וציין מהם 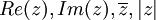 . הביטוי הינו:
. הביטוי הינו: 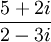
פתרון
נכפול בצמוד למכנה למעלה ולמטה 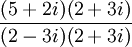 .
.
נעצור לרגע להבין את הפורמליות של מה שאנחנו עושים. הרי 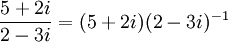 וכעת רשמנו
וכעת רשמנו ![(5+2i)(2+3i)[(2-3i)^{-1}(2+3i)^{-1}]](/images/math/6/9/7/697397e9967c04c9e9a05cd7787d074e.png)
לפיכך נקבל 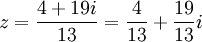
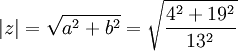
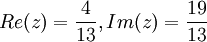
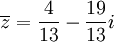
תכונות של מרוכבים
משפט דמואבר
ידוע שניתן להציג כל מספר מרוכב באופן יחיד בצורה 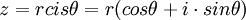 כאשר r הוא ממשי אי-שלילי (המציין את המרחב בראשית הצירים ושווה ל |z|) והזווית
כאשר r הוא ממשי אי-שלילי (המציין את המרחב בראשית הצירים ושווה ל |z|) והזווית 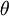 נמדדת נגד כיוון השעון מהקרן החיובית של ציר x.
נמדדת נגד כיוון השעון מהקרן החיובית של ציר x.
משפט דמואבר אומר ש 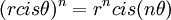
תרגיל 3.8 א'
חשב את 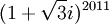
פתרון
דבר ראשון נעבור לצורה קוטבית 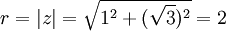
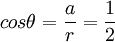
ולכן 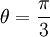
ביחד 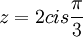 ולכן
ולכן 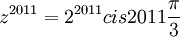 מכיוון שגם הסינוס וגם הקוסינוס הם ממחזור שני פאי, זה שווה ל
מכיוון שגם הסינוס וגם הקוסינוס הם ממחזור שני פאי, זה שווה ל
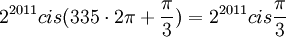
מערכות משוואות לינאריות
מערכות משוואות לינאריות בn משתנים עם m משוואות הינה מערכת מהצורה
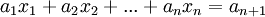
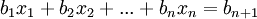
...
(סה"כ m משוואות)
ניתן להציג כל מערכת כזו באמצעות טבלת מספרים הנקראת מטריצה. לדוגמא:
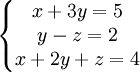
את המערכת הנ"ל נייצג באמצעות המטריצה
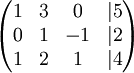
ניתן להבחין במספר פעולות שלא ישנו את פתרונות מערכת המשוואות:
- כפל שני אגפי המשוואה במספר שונה מאפס (שקול לכפל שורה במטריצה במספר שונה מאפס)
- חיבור שני אגפי משוואה אחת כפול קבוע, לשני אגפי משוואה שנייה (שקול לחיבור שורה אחת כפול קבוע במטריצה לשורה אחרת)
- החלפת סדר המשוואות (שקול להחלפת סדר השורות במטריצה)
דירוג גאוס
איבר מוביל/פותח/ציר הינו האיבר הראשון בשורה ששונה מאפס (משמאל לימין). מטריצה נקראת מדורגת אם מתחת לכל איבר מוביל שלה יש אפסים בלבד וכל איבר מוביל נמצא מימין לאיברים המובילים הקודמים. בנוסף, יש את הדרישה כי שורות אפסים (אם קיימות) נמצאות בסוף. מטריצה נקראת מדורגת קנונית אם היא מדורגת, ובנוסף יש אפסים מעל לכל איבר מוביל והאיברים המובילים חייבים להיות שווים למספר אחד.
הערה: לכל מטריצה קיימת צורה קנונית יחידה.
כעת נלמד אלגוריתם המאפשר לנו לפתור מערכת משוואות לינארית באמצעות הצורה המטריצית שלה (בפרט, נדרג את המטריצה לצורתה הקנונית). תהליך זה נקרא אלגוריתם לדירוג גאוס.
תרגיל 1.5 סעיף ב'
פתור את המערכת הבאה מעל 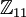 .
.
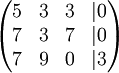
פתרון
נכפול את השורה הראשונה ב9 ואת השנייה והשלישית ב8. זכרו שכל הפעולות הן מודולו 11:
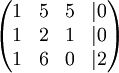
נחסר את השורה הראשונה מן השורות השנייה והשלישית.
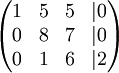
נכפול את השורה השנייה ב7
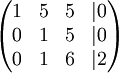
נחסר את השורה השנייה מהשלישית לקבל
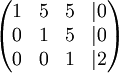
ולכן הפיתרון הינו: 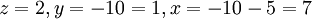
מספר פתרונות
- נביט בצורה המדורגת של המטריצה.
- משתנה אשר בעמודה שלו בצורה המדורגת יש איבר מוביל (איבר ראשון משמאל בשורה, ששונה מאפס), נקרא משתנה תלוי.
- שאר המשתנים נקראים משתנים חופשיים.
- אם בצורה המדורגת יש שורת סתירה, אזי אין פתרונות למערכת.
- אם אין שורת סתירה בצורה המדורגת, מספר הפתרונות של המערכת הוא מספר האיברים בשדה בחזקת מספר המשתנים החופשיים.
- בפרט, אם אין שורת סתירה ואין משתנים חופשיים אז יש פתרון יחיד.
- בפרט, אם אין שורת סתירה, יש משתנים חופשיים ויש אינסוף מספרים בשדה אז יש אינסוף פתרונות.
תרגיל
מצא לאילו ערכים של הפרמטרים a,t יש למערכת פתרון יחיד, אין פתרון, או אינסוף פתרונות. במקרה של אינסוף פתרונות מצא את הפתרון הכללי.
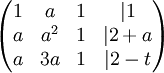
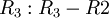
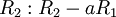
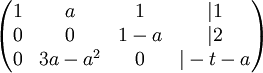
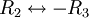
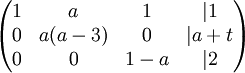
כעת נניח 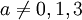 . נבצע פעולות שחוקיות רק תחת ההנחה הזו, ולאחר מכן לחזור לנקודה הזו בדיוק ונפתור את המקרים
. נבצע פעולות שחוקיות רק תחת ההנחה הזו, ולאחר מכן לחזור לנקודה הזו בדיוק ונפתור את המקרים 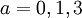 בצורה חוקית.
בצורה חוקית.
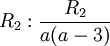
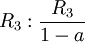
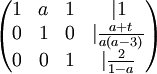
במקרה זה אין משתנים חופשיים ויש פתרון יחיד.
נחזור למקרים האחרים:
- נניח a=0 ונציב את הפרמטר הזו בנקודה בה עצרנו. נקבל:
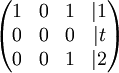
אנו מקבלים משוואה מהצורה 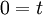 .
.
- אם
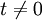 זו סתירה ולכן אין אף פתרון שיקיים את כל משוואות המערכת (כי משוואה זו לעולם לא תתקיים).
זו סתירה ולכן אין אף פתרון שיקיים את כל משוואות המערכת (כי משוואה זו לעולם לא תתקיים). - אם t=0 מקבלים משתנה חופשי, ואינסוף פתרונות: נציב במקום המשתנה החופשי פרמטר s ונקבל:
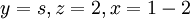 ולכן סה"כ הפתרון הכללי הוא מהצורה
ולכן סה"כ הפתרון הכללי הוא מהצורה 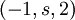
- אם
- נניח a=1:
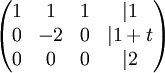
השורה האחרונה הינה שורת סתירה ולכן אין פתרונות במצב זה.
- נניח a=3:
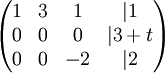
- אם
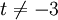 יש שורת סתירה ואין פתרון למערכת
יש שורת סתירה ואין פתרון למערכת - אם t=3 הפתרון הכללי הוא מהצורה
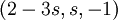
- אם