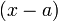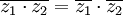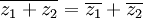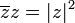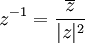הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/1"
(←מרוכבים) |
|||
| (109 גרסאות ביניים של 9 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול|חזרה למערכי התרגול]] | ||
| + | |||
=שיעור ראשון= | =שיעור ראשון= | ||
| − | ==שדות | + | |
| − | + | ==שדות (מה שנעשה בהרצאה אפשר לדלג)== | |
| − | + | הגדרה: [[שדה]]. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
===תרגיל 1.3 סעיף ג'=== | ===תרגיל 1.3 סעיף ג'=== | ||
| − | יהי שדה <math>\mathbb{F}</math>. | + | [בד"כ נעשה בהרצאה!] |
| + | |||
| + | יהי שדה <math>\mathbb{F}</math>. הוכיחו את הטענה הבאה: <math>\forall a\in\mathbb{F}:0\cdot a = 0</math>, כאשר <math>0</math> הינו הסימון לאיבר הנייטרלי החיבורי. | ||
====פתרון==== | ====פתרון==== | ||
| − | |||
| + | ראשית נשים לב שלפי הנתונים ניתן להניח שאקסיומות השדה מתקיימות. | ||
| − | + | יהא <math>a\in \mathbb{F} </math>. צריך להוכיח כי <math>0\cdot a = 0</math> | |
| − | + | לפי תכונה (4) [ניטרליות <math>0</math> לחיבור] מתקיים ש <math>0+0=0</math> | |
| − | + | לכן <math>0\cdot a = (0+0)\cdot a</math> | |
| − | לפי תכונה ( | + | לפי תכונה (7) [פילוג] מתקיים בנוסף ש<math>0\cdot a = (0+0)\cdot a = 0\cdot a + 0\cdot a</math> (השתמשנו בעצם בתכונה (7) לאחר שהפעלנו עליה את תכונה (2)) |
| − | לפי תכונה ( | + | לפי תכונה (5) [קיום נגדי] לאיבר <math>0\cdot a \in\mathbb{F}</math> קיים איבר נגדי. נחבר אותו לשני צידי המשוואה לקבל <math>0\cdot a + (-(0\cdot a)) = (0\cdot a + 0\cdot a) + (-(0\cdot a))</math> |
| + | 4444 | ||
| + | לפי תכונה (3) [קיבוציות] ניתן להחליף את סדר הסוגריים מימין ולקבל | ||
| + | <math>0\cdot a + (-(0\cdot a)) = 0\cdot a + (0\cdot a + (-(0\cdot a)))</math> | ||
| − | |||
| + | עוד לפי תכונה (5) [תכונת הנגדי] יחד עם תכונה (4) [נטרליות 0 לחיבור] מתקיים ש<math>0 = 0\cdot a</math> בדיוק כפי שרצינו להוכיח. | ||
| + | |||
| + | ===תרגיל=== | ||
| + | הוכיחו שבשדה ל0 אין הופכי. | ||
| + | |||
| + | ===פתרון=== | ||
| + | מכיוון ש0 כפול דבר שווה ל0. | ||
===תרגיל 1.3 סעיף ו'=== | ===תרגיל 1.3 סעיף ו'=== | ||
| − | יהי שדה <math>\mathbb{F}</math>. | + | יהי שדה <math>\mathbb{F}</math>. הוכיחו את הטענה הבאה: <math>\forall a\in\mathbb{F}:-(-a)=a</math>. (כלומר, הנגדי של הנגדי הוא האיבר עצמו) |
====פתרון==== | ====פתרון==== | ||
| − | + | יהא a בשדה צריך להוכיח כי <math>(-a)+a=0</math> [זה הגדרת נגדי]. | |
| + | כיוון החיבור חילופי נקבל כי <math>(-a)+a=a+(-a)</math>. כיוון ש <math>a+(-a)=0</math> לפי הגדרת נגדי של a, סיימנו. | ||
| − | + | ===תרגיל 1.3 סעיף ז'=== | |
| + | יהי שדה <math>\mathbb{F}</math>. הוכיחו את הטענה הבאה: <math>\forall a\in\mathbb{F}:(-1)\cdot a=-a</math>. (כלומר הנגדי של האיבר הנייטרלי הכפלי כפול a הינו הנגדי של a) | ||
| + | ====פתרון==== | ||
| + | <math>-a</math> זה סימון לנגדי של <math>a</math>. לכן מה שבעצם צריך להוכיח זה ש- <math>(-1)\cdot a</math> הוא הנגדי של <math>a</math>, לכן הם שווים (נגדי יש אחד). | ||
| − | + | מתוך תכונות (7),(5) וסעיף ג' שהוכחנו לעיל, <math>0=0\cdot a = (1+(-1))\cdot a = 1\cdot a + (-1)\cdot a</math> | |
| − | + | לפי תכונה (4) קיבלנו <math>0=a+(-1)\cdot a</math> | |
| − | + | לכן קיבלנו ש- <math>(-1)\cdot a</math> הוא הנגדי של <math>a</math> כפי שרצינו. | |
| + | ===תרגיל=== | ||
| + | הוכיחו שבשדה מתקיים כי <math>(-1)(-1)=1</math> | ||
| + | ===תרגיל === | ||
| + | בד"כ נעשה בהרצאה! | ||
| + | יהא <math>\mathbb{F}</math> שדה. הוכיחו כי אין לו מחלקי אפס. כלומר לא קיימים <math>a,b\in \mathbb{F}</math> שונים מאפס כך ש <math>ab=0</math> (באופן שקול: אם <math>ab=0</math> אז בהכרח אחד מהם שווה 0) | ||
| − | + | ====פתרון==== | |
| + | נניח <math>ab=0</math>. צ"ל שאחד מהם אפס. | ||
| + | אם <math>a=0</math> סיימנו | ||
| + | אחרת <math>a\neq 0 </math> ולכן קיים לו הופכי <math>a^{-1}</math>. נכפיל את ההופכי של a בשני האגפים ונקבל | ||
| + | <math>b=a^{-1}ab=a^{-1}0=0</math> וסיימנו. | ||
| − | + | ===תרגיל 2.3 סעיף א'=== | |
| − | ===תרגיל | + | [בד"כ נעשה בהרצאה!] |
| − | + | יש להוכיח שקבוצת הטבעיים <math>\mathbb{N}=\{1,2,3,....\}</math> אינה שדה. | |
====פתרון==== | ====פתרון==== | ||
| − | + | אין איבר נייטרלי לחיבור: <math>\forall n,k\in\mathbb{N}:n+k>n</math>, ואילו האיבר הנייטרלי היה צריך לקיים <math>n+0=n</math>. | |
| − | |||
| + | ===תרגיל=== | ||
| − | + | הוכיחו שבשה יש רק איבר אחד שנטרלי לכפל. (כלומר, איבר היחידה הוא יחיד) | |
| + | ===תרגיל=== | ||
| − | + | הוכיחו שבשדה לכל איבר יש הופכי יחיד. | |
| − | יש | + | |
| − | ==== | + | ===תרגיל=== |
| − | + | ||
| + | הוכיחו שבשדה מתקיים צמצום בכפל. כלומר, אם ab=ac כאשר a לא 0, אז b=c. | ||
===תרגיל 2.3 סעיף ג'=== | ===תרגיל 2.3 סעיף ג'=== | ||
| − | + | [בד"כ נעשה בהרצאה!] | |
| + | הגדרה: נגדיר את הקבוצה הבאה: <math>\mathbb{Z}_n=\{\overline{0},\overline{1},\overline{2},...,\overline{n-1}\}</math>. | ||
| + | |||
| + | עובדה: עבור n=p ראשוני הקבוצה <math>\mathbb{Z}_p=\{\overline{0},\overline{1},\overline{2},...,\overline{p-1}\}</math> הינה שדה ביחס לחיבור וכפל מודלו p. הניטרלי לחיבור הוא 0 והנטרלי לכפל הוא 1. למשל <math>\mathbb{Z}_3=\{\overline{0},\overline{1},\overline{2}\}</math> | ||
| − | + | תרגיל: הוכיחו כי ש<math>\mathbb{Z}_n</math> אינו שדה כאשר n מספר פריק (כלומר קיימים טבעיים כך ש n=mk) | |
| + | ביחס לפעולות החיבור והכפל מודולו n. | ||
====פתרון==== | ====פתרון==== | ||
| − | לפי הנתונים קיימים <math>k,m<n</math> כך ש <math>mk=n</math>. לפיכך, לפי ההגדרה, | + | לפי הנתונים קיימים <math>0<k,m<n</math> כך ש <math>mk=n</math>. לפיכך, לפי ההגדרה, |
<math>\overline{m}\overline{k}=n\mod{n} =\overline{0}</math>. | <math>\overline{m}\overline{k}=n\mod{n} =\overline{0}</math>. | ||
| − | + | כלומר יש מחלקי אפס. כיוון שבשדה אין מחלקי אפס נסיק כי <math>\mathbb{Z}_n</math> אינו שדה במקרה זה. | |
| − | + | ||
| − | + | ||
| − | <math>\ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
===תרגיל 2.6=== | ===תרגיל 2.6=== | ||
| שורה 113: | שורה 131: | ||
====פתרון==== | ====פתרון==== | ||
| − | לא. ניקח <math>(0+i)\cdot(1+0\cdot i)=0</math> כלומר יש לנו איברים שונים מאפס שמכפלתם הינה אפס. | + | לא. ניקח <math>(0+i)\cdot(1+0\cdot i)=0</math> כלומר יש לנו איברים שונים מאפס שמכפלתם הינה אפס. כלומר מחלקי אפס אבל בשדה אין מחלקי אפס! |
===תרגיל 3.4=== | ===תרגיל 3.4=== | ||
| שורה 139: | שורה 157: | ||
*<math>\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}</math> | *<math>\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}</math> | ||
| + | |||
| + | |||
| + | *<math>\overline{z}z=|z|^2</math> | ||
| שורה 144: | שורה 165: | ||
===משפט דמואבר=== | ===משפט דמואבר=== | ||
| − | ידוע שניתן להציג כל מספר מרוכב באופן יחיד בצורה <math>z=rcis\theta = r(cos\theta + i\cdot sin\theta)</math>. משפט דמואבר אומר ש <math>(rcis\theta)^n=r^ncis(n\theta)</math> | + | [אפשר לדלג] |
| + | |||
| + | ידוע שניתן להציג כל מספר מרוכב באופן יחיד בצורה <math>z=rcis\theta = r(cos\theta + i\cdot sin\theta)</math> כאשר r הוא ממשי אי-שלילי (המציין את המרחק מראשית הצירים ושווה ל |z|) והזווית <math>\theta</math> נמדדת נגד כיוון השעון מהקרן החיובית של ציר x. צורה זו נקראת הצורה הקוטבית של מספר מרוכב z. (ההצגה של המספר המרוכב z=a+bi, נקראת ההצגה הקרטזית שלו) | ||
| + | |||
| + | משפט דמואבר אומר ש <math>(rcis\theta)^n=r^ncis(n\theta)</math> | ||
===תרגיל 3.8 א'=== | ===תרגיל 3.8 א'=== | ||
| − | חשב את <math>(1+\sqrt{3}i)^2011</math> | + | חשב את <math>(1+\sqrt{3}i)^{2011}</math> |
===פתרון=== | ===פתרון=== | ||
| − | דבר ראשון נעבור לצורה קוטבית <math>r=|z|=\sqrt{1^2+(\sqrt{3})^2}=2</math> | + | דבר ראשון נעבור לצורה קוטבית. בהנתן מספר מרוכב z=a+bi המעבר לצורה הקוטבית שלו <math>z=r\cdot cis(\theta)</math> מתבצע על ידי |
| + | <math>r=|z|, cos\theta = \frac{a}{r}</math> | ||
| + | |||
| + | אצלנו בשאלה | ||
| + | |||
| + | |||
| + | <math>r=|z|=\sqrt{1^2+(\sqrt{3})^2}=2</math> | ||
| + | |||
| + | <math>cos\theta = \frac{a}{r}=\frac{1}{2}</math> | ||
| + | |||
| + | ולכן <math>\theta = \frac{\pi}{3}</math> | ||
ביחד <math>z=2cis\frac{\pi}{3}</math> ולכן <math>z^{2011}=2^{2011} cis 2011\frac{\pi}{3}</math> מכיוון שגם הסינוס וגם הקוסינוס הם ממחזור שני פאי, זה שווה ל | ביחד <math>z=2cis\frac{\pi}{3}</math> ולכן <math>z^{2011}=2^{2011} cis 2011\frac{\pi}{3}</math> מכיוון שגם הסינוס וגם הקוסינוס הם ממחזור שני פאי, זה שווה ל | ||
| − | <math> | + | <math>2^{2011}cis(335\cdot 2\pi+\frac{\pi}{3})=2^{2011}cis\frac{\pi}{3}</math> |
| + | |||
| + | === תרגיל === | ||
| + | פתרון את המשוואה <math>z^5=3+4i</math> | ||
| + | |||
| + | === תרגיל === | ||
| + | מצאו דרך פשוטה לסובב נקודה במישור <math>\left(a,b\right)</math> בזווית <math>\theta</math> (כלומר למצוא את הנקודה במישור המתקבלת לאחר הסיבוב) | ||
| + | |||
| + | פתרון: | ||
| + | |||
| + | נחשוב במרוכבים על האיבר <math>a+bi</math> ונכפיל אותו ב <math>cis(\theta)</math> | ||
| − | == | + | === תרגיל === |
| − | + | חשבו את הסכום <math>\cos(1)+\cdots +\cos(n)</math> | |
| − | + | פתרון: | |
| − | <math> | + | ניעזר במרוכבים: <math>\sum_{k=1}^{n}\cos(k)=\text{Re}\left(\sum_{k=1}^{n}\text{cis}(k)\right)=\text{Re}\left(\sum_{k=1}^{n}\text{cis}(1)^{k}\right)</math> |
| − | . | + | ===תרגיל (חשוב) === |
| + | '''לרוב נעשה בהרצאה''' - ולכן הצעה: הוכיחו שלפולינום <math>p(x)=1+2x+3x^2+4x^3+5x^4+6x^5</math> יש שורש ממשי (בלי להזכיר את המשפט מההרצאה, לוודא שהם זוכרים לבד). אחרי זה אפשר להזכיר, אם נדרש, את ההגדרה והמשפט, ולעבור למסקנה. | ||
| − | ( | + | הגדרה: פולינום עם מקדמים משדה <math>\mathbb{F}</math> ומשתנה x הוא <math>a_0+a_1x+a_2x^2+\cdots +a_nx^n</math> כאשר <math>a_i</math> קבועים מהשדה. |
| + | בהיתן פולינום <math>p(x)</math> ואיבר בשדה <math>a</math> נוכל להציב את a בפולינום לקבל איבר בשדה <math>p(a)=\sum_{i=0}^{n}a_ia^i</math>. | ||
| + | עוד נגדיר: a יקרא שורש של פולינום <math>p(x)</math> אם <math>p(a)=0</math> | ||
| + | יהא <math>p(x)</math> פולינום עם מקדמים ממשיים. הוכיחו שאם <math>z\in \mathbb{C}</math> שורש של פולינום <math>p(x)</math> אזי גם <math>\bar{z}</math> שורש של אותו פולינום. | ||
| − | + | הוכחה: בשימוש תכונות הצמוד. | |
| − | <math>\left | + | ==== ~מסקנה==== |
| − | x | + | הסיקו (קצת בנפנופי ידיים, העיקר התובנה) שכל פולינום ממשי ניתן לפירוק לגורמים מדרגה קטנה שווה 2. היעזרו במשפט היסודי של האלגברה: כל פולינום מרוכב מדרגה <math>n</math> ניתן לפירוק למכפלה של <math>n</math> גורמים בדיוק מהצורה <math>\left(x-a\right)</math> |
| − | + | ||
| − | + | ||
| − | + | ||
גרסה אחרונה מ־17:30, 5 ביולי 2021
תוכן עניינים
שיעור ראשון
שדות (מה שנעשה בהרצאה אפשר לדלג)
הגדרה: שדה.
תרגיל 1.3 סעיף ג'
[בד"כ נעשה בהרצאה!]
יהי שדה 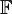 . הוכיחו את הטענה הבאה:
. הוכיחו את הטענה הבאה: 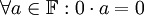 , כאשר
, כאשר 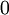 הינו הסימון לאיבר הנייטרלי החיבורי.
הינו הסימון לאיבר הנייטרלי החיבורי.
פתרון
ראשית נשים לב שלפי הנתונים ניתן להניח שאקסיומות השדה מתקיימות.
יהא 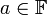 . צריך להוכיח כי
. צריך להוכיח כי 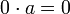
לפי תכונה (4) [ניטרליות 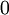 לחיבור] מתקיים ש
לחיבור] מתקיים ש 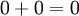
לכן 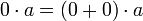
לפי תכונה (7) [פילוג] מתקיים בנוסף ש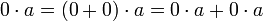 (השתמשנו בעצם בתכונה (7) לאחר שהפעלנו עליה את תכונה (2))
(השתמשנו בעצם בתכונה (7) לאחר שהפעלנו עליה את תכונה (2))
לפי תכונה (5) [קיום נגדי] לאיבר 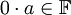 קיים איבר נגדי. נחבר אותו לשני צידי המשוואה לקבל
קיים איבר נגדי. נחבר אותו לשני צידי המשוואה לקבל 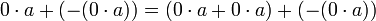
4444
לפי תכונה (3) [קיבוציות] ניתן להחליף את סדר הסוגריים מימין ולקבל
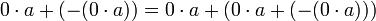
עוד לפי תכונה (5) [תכונת הנגדי] יחד עם תכונה (4) [נטרליות 0 לחיבור] מתקיים ש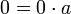 בדיוק כפי שרצינו להוכיח.
בדיוק כפי שרצינו להוכיח.
תרגיל
הוכיחו שבשדה ל0 אין הופכי.
פתרון
מכיוון ש0 כפול דבר שווה ל0.
תרגיל 1.3 סעיף ו'
יהי שדה 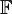 . הוכיחו את הטענה הבאה:
. הוכיחו את הטענה הבאה: 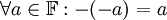 . (כלומר, הנגדי של הנגדי הוא האיבר עצמו)
. (כלומר, הנגדי של הנגדי הוא האיבר עצמו)
פתרון
יהא a בשדה צריך להוכיח כי 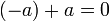 [זה הגדרת נגדי].
[זה הגדרת נגדי].
כיוון החיבור חילופי נקבל כי 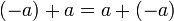 . כיוון ש
. כיוון ש 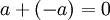 לפי הגדרת נגדי של a, סיימנו.
לפי הגדרת נגדי של a, סיימנו.
תרגיל 1.3 סעיף ז'
יהי שדה 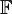 . הוכיחו את הטענה הבאה:
. הוכיחו את הטענה הבאה: 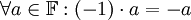 . (כלומר הנגדי של האיבר הנייטרלי הכפלי כפול a הינו הנגדי של a)
. (כלומר הנגדי של האיבר הנייטרלי הכפלי כפול a הינו הנגדי של a)
פתרון
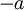 זה סימון לנגדי של
זה סימון לנגדי של 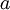 . לכן מה שבעצם צריך להוכיח זה ש-
. לכן מה שבעצם צריך להוכיח זה ש- 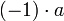 הוא הנגדי של
הוא הנגדי של 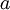 , לכן הם שווים (נגדי יש אחד).
, לכן הם שווים (נגדי יש אחד).
מתוך תכונות (7),(5) וסעיף ג' שהוכחנו לעיל, 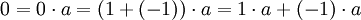
לפי תכונה (4) קיבלנו 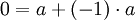
לכן קיבלנו ש- 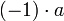 הוא הנגדי של
הוא הנגדי של 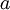 כפי שרצינו.
כפי שרצינו.
תרגיל
הוכיחו שבשדה מתקיים כי 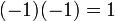
תרגיל
בד"כ נעשה בהרצאה!
יהא 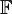 שדה. הוכיחו כי אין לו מחלקי אפס. כלומר לא קיימים
שדה. הוכיחו כי אין לו מחלקי אפס. כלומר לא קיימים 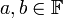 שונים מאפס כך ש
שונים מאפס כך ש 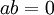 (באופן שקול: אם
(באופן שקול: אם 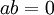 אז בהכרח אחד מהם שווה 0)
אז בהכרח אחד מהם שווה 0)
פתרון
נניח 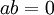 . צ"ל שאחד מהם אפס.
אם
. צ"ל שאחד מהם אפס.
אם 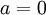 סיימנו
אחרת
סיימנו
אחרת 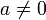 ולכן קיים לו הופכי
ולכן קיים לו הופכי 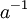 . נכפיל את ההופכי של a בשני האגפים ונקבל
. נכפיל את ההופכי של a בשני האגפים ונקבל
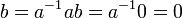 וסיימנו.
וסיימנו.
תרגיל 2.3 סעיף א'
[בד"כ נעשה בהרצאה!]
יש להוכיח שקבוצת הטבעיים 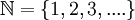 אינה שדה.
אינה שדה.
פתרון
אין איבר נייטרלי לחיבור: 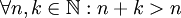 , ואילו האיבר הנייטרלי היה צריך לקיים
, ואילו האיבר הנייטרלי היה צריך לקיים 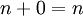 .
.
תרגיל
הוכיחו שבשה יש רק איבר אחד שנטרלי לכפל. (כלומר, איבר היחידה הוא יחיד)
תרגיל
הוכיחו שבשדה לכל איבר יש הופכי יחיד.
תרגיל
הוכיחו שבשדה מתקיים צמצום בכפל. כלומר, אם ab=ac כאשר a לא 0, אז b=c.
תרגיל 2.3 סעיף ג'
[בד"כ נעשה בהרצאה!]
הגדרה: נגדיר את הקבוצה הבאה: 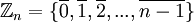 .
.
עובדה: עבור n=p ראשוני הקבוצה 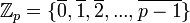 הינה שדה ביחס לחיבור וכפל מודלו p. הניטרלי לחיבור הוא 0 והנטרלי לכפל הוא 1. למשל
הינה שדה ביחס לחיבור וכפל מודלו p. הניטרלי לחיבור הוא 0 והנטרלי לכפל הוא 1. למשל 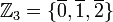
תרגיל: הוכיחו כי ש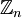 אינו שדה כאשר n מספר פריק (כלומר קיימים טבעיים כך ש n=mk)
ביחס לפעולות החיבור והכפל מודולו n.
אינו שדה כאשר n מספר פריק (כלומר קיימים טבעיים כך ש n=mk)
ביחס לפעולות החיבור והכפל מודולו n.
פתרון
לפי הנתונים קיימים 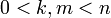 כך ש
כך ש 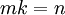 . לפיכך, לפי ההגדרה,
. לפיכך, לפי ההגדרה,
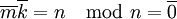 .
.
כלומר יש מחלקי אפס. כיוון שבשדה אין מחלקי אפס נסיק כי 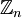 אינו שדה במקרה זה.
אינו שדה במקרה זה.
תרגיל 2.6
הסבר מדוע 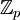 אינו תת שדה של
אינו תת שדה של 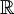
פתרון
תת שדה הינו תת קבוצה של איברים, תחת אותן פעולות כמו בשדה. לכן 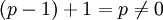 ולכן אין סגירות לחיבור וזה אינו תת שדה.
ולכן אין סגירות לחיבור וזה אינו תת שדה.
מרוכבים
נגדיר מרוכבים, נראה שרוב תכונות השדה הן טריוויאליות פרט לקיום ההופכי וגם זה ניתן להוכחה.
תרגיל 3.2
אם נשנה את פעולת כפל המרוכבים לפעולה הבאה: 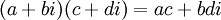 , האם קבוצת המרוכבים תשאר שדה?
, האם קבוצת המרוכבים תשאר שדה?
פתרון
לא. ניקח 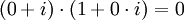 כלומר יש לנו איברים שונים מאפס שמכפלתם הינה אפס. כלומר מחלקי אפס אבל בשדה אין מחלקי אפס!
כלומר יש לנו איברים שונים מאפס שמכפלתם הינה אפס. כלומר מחלקי אפס אבל בשדה אין מחלקי אפס!
תרגיל 3.4
הצג את הביטוי הבא בצורה 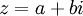 וציין מהם
וציין מהם 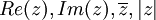 . הביטוי הינו:
. הביטוי הינו: 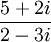
פתרון
נכפול בצמוד למכנה למעלה ולמטה 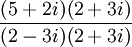 .
.
נעצור לרגע להבין את הפורמליות של מה שאנחנו עושים. הרי 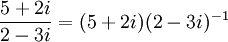 וכעת רשמנו
וכעת רשמנו ![(5+2i)(2+3i)[(2-3i)^{-1}(2+3i)^{-1}]](/images/math/6/9/7/697397e9967c04c9e9a05cd7787d074e.png)
לפיכך נקבל 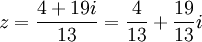
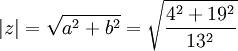
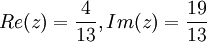
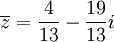
תכונות של מרוכבים
משפט דמואבר
[אפשר לדלג]
ידוע שניתן להציג כל מספר מרוכב באופן יחיד בצורה 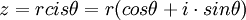 כאשר r הוא ממשי אי-שלילי (המציין את המרחק מראשית הצירים ושווה ל |z|) והזווית
כאשר r הוא ממשי אי-שלילי (המציין את המרחק מראשית הצירים ושווה ל |z|) והזווית 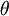 נמדדת נגד כיוון השעון מהקרן החיובית של ציר x. צורה זו נקראת הצורה הקוטבית של מספר מרוכב z. (ההצגה של המספר המרוכב z=a+bi, נקראת ההצגה הקרטזית שלו)
נמדדת נגד כיוון השעון מהקרן החיובית של ציר x. צורה זו נקראת הצורה הקוטבית של מספר מרוכב z. (ההצגה של המספר המרוכב z=a+bi, נקראת ההצגה הקרטזית שלו)
משפט דמואבר אומר ש 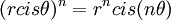
תרגיל 3.8 א'
חשב את 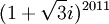
פתרון
דבר ראשון נעבור לצורה קוטבית. בהנתן מספר מרוכב z=a+bi המעבר לצורה הקוטבית שלו 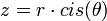 מתבצע על ידי
מתבצע על ידי
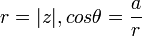
אצלנו בשאלה
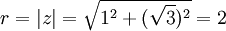
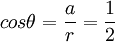
ולכן 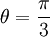
ביחד 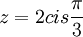 ולכן
ולכן 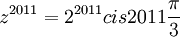 מכיוון שגם הסינוס וגם הקוסינוס הם ממחזור שני פאי, זה שווה ל
מכיוון שגם הסינוס וגם הקוסינוס הם ממחזור שני פאי, זה שווה ל
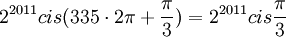
תרגיל
פתרון את המשוואה 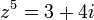
תרגיל
מצאו דרך פשוטה לסובב נקודה במישור 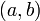 בזווית
בזווית 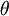 (כלומר למצוא את הנקודה במישור המתקבלת לאחר הסיבוב)
(כלומר למצוא את הנקודה במישור המתקבלת לאחר הסיבוב)
פתרון:
נחשוב במרוכבים על האיבר 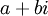 ונכפיל אותו ב
ונכפיל אותו ב 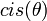
תרגיל
חשבו את הסכום 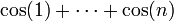
פתרון:
ניעזר במרוכבים: 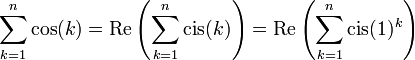
תרגיל (חשוב)
לרוב נעשה בהרצאה - ולכן הצעה: הוכיחו שלפולינום 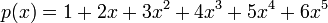 יש שורש ממשי (בלי להזכיר את המשפט מההרצאה, לוודא שהם זוכרים לבד). אחרי זה אפשר להזכיר, אם נדרש, את ההגדרה והמשפט, ולעבור למסקנה.
יש שורש ממשי (בלי להזכיר את המשפט מההרצאה, לוודא שהם זוכרים לבד). אחרי זה אפשר להזכיר, אם נדרש, את ההגדרה והמשפט, ולעבור למסקנה.
הגדרה: פולינום עם מקדמים משדה 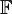 ומשתנה x הוא
ומשתנה x הוא 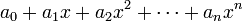 כאשר
כאשר 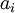 קבועים מהשדה.
בהיתן פולינום
קבועים מהשדה.
בהיתן פולינום 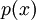 ואיבר בשדה
ואיבר בשדה 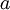 נוכל להציב את a בפולינום לקבל איבר בשדה
נוכל להציב את a בפולינום לקבל איבר בשדה 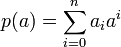 .
עוד נגדיר: a יקרא שורש של פולינום
.
עוד נגדיר: a יקרא שורש של פולינום 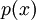 אם
אם 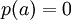
יהא 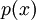 פולינום עם מקדמים ממשיים. הוכיחו שאם
פולינום עם מקדמים ממשיים. הוכיחו שאם 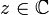 שורש של פולינום
שורש של פולינום 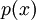 אזי גם
אזי גם 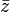 שורש של אותו פולינום.
שורש של אותו פולינום.
הוכחה: בשימוש תכונות הצמוד.
~מסקנה
הסיקו (קצת בנפנופי ידיים, העיקר התובנה) שכל פולינום ממשי ניתן לפירוק לגורמים מדרגה קטנה שווה 2. היעזרו במשפט היסודי של האלגברה: כל פולינום מרוכב מדרגה 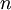 ניתן לפירוק למכפלה של
ניתן לפירוק למכפלה של 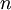 גורמים בדיוק מהצורה
גורמים בדיוק מהצורה