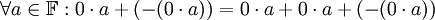88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/1

שיעור ראשון

שדות

הגדרה

קבוצה 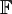$\mathbb{F}$ עם זוג פעולות בינאריות הנקראות כפל וחיבור 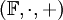$(\mathbb{F},\cdot,+)$ נקראת שדה אם מתקיימות התכונות הבאות:

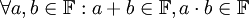1. סגירות- $\forall a,b\in\mathbb{F}:a+b\in\mathbb{F},a\cdot b\in\mathbb{F}$. (שימו לב שזה בסך הכל אומר שתוצאת הפעולות הבינאריות נשארת בשדה)
2. קומוטטיביות/חילופיות- $\forall a,b\in\mathbb{F}:a+b=b+a,a\cdot b = b\cdot a$
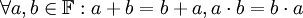
3. אסוציאטיביות- $\forall a,b,c\in\mathbb{F}:(a+b)+c=a+(b+c),(a\cdot b)\cdot c = a\cdot(b\cdot c)$
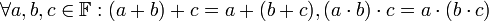
4. קיום איברים נייטרליים- קיימים איברים שנסמנם 1,0 המקיימים 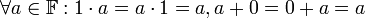$\forall a\in\mathbb{F}:1\cdot a = a \cdot 1 = a, a+0=0+a=a$. בנוסף מתקיים ש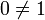$0\neq 1$
5. קיום איבר נגדי לחיבור- לכל איבר a קיים איבר שנסמנו 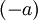$(-a)$ כך שמתקיים 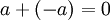$a+(-a)=0$. לצורך קיצור הכתיבה נסמן 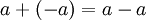$a+(-a)=a-a$ (פעולת החיסור היא פשוט חיבור לנגדי)
6. קיום איבר הופכי לכפל- לכל איבר a קיים איבר שנסמנו 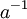$a^{-1}$ כך שמתקיים 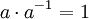$a\cdot a^{-1} = 1$. שיטה נפוצה לסימון פעולה זו הינה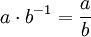 $a\cdot b^{-1}=\frac{a}{b}$
7. דיסטריביוטיביות/פילוג- 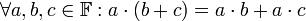$\forall a,b,c\in\mathbb{F}: a\cdot (b+c)=a\cdot b +a\cdot c$. שימו לב שזו התכונה היחידה המקשרת בין הכפל לבין החיבור

תרגיל

יהי שדה 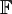$\mathbb{F}$. הוכח שניתן לגזור מתכונות השדה את הטענה הבאה: 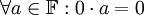$\forall a\in\mathbb{F}:0\cdot a = 0$, כאשר 0 הינו הסימון לאיבר הנייטרלי החיבורי.

פתרון

ראשית נשים לב שלפי הנתונים ניתן להניח שתכונות השדה מתקיימות.

לפי תכונה (4) מתקיים ש 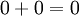$0+0=0$

לכן 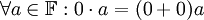$\forall a\in\mathbb{F}:0\cdot a = (0+0)a$

לפי תכונה (7) מתקיים בנוסף ש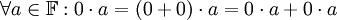$\forall a\in\mathbb{F}:0\cdot a = (0+0)\cdot a = 0\cdot a + 0\cdot a$ (השתמשנו בעצם בתכונה (7) לאחר שהפעלנו עליה את תכונה (2))

לפי תכונה (5) לאיבר 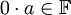$0\cdot a \in\mathbb{F}$ קיים איבר נגדי. נחבר אותו לשני צידי המשוואה לקבל $\forall a\in\mathbb{F}:0\cdot a + (-(0\cdot a)) = 0\cdot a + 0\cdot a + (-(0\cdot a))$