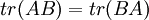הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/9"
אחיה בר-און (שיחה | תרומות) (←תרגיל חשוב!) |
|||
| (38 גרסאות ביניים של 6 משתמשים אינן מוצגות) | |||
| שורה 3: | שורה 3: | ||
==מטריצות מייצגות== | ==מטריצות מייצגות== | ||
| − | '''הגדרה.''' תהי <math>T:V\rightarrow W</math> העתקה לינארית, ויהיו <math>E,F</math> בסיסים ל<math>V,W</math> בהתאמה. נסמן <math>E=\{v_1,...,v_n\}</math>. אזי '''המטריצה המייצגת''' את T מבסיס E לבסיס F הינה המטריצה שעמודותיה הן הקואורדינטות לפי הבסיס F של התמונות של איברי הבסיס E מסמנים | + | '''הגדרה.''' תהי <math>T:V\rightarrow W</math> העתקה לינארית, ויהיו <math>E,F</math> בסיסים ל<math>V,W</math> בהתאמה. נסמן <math>E=\{v_1,...,v_n\}</math>. אזי '''המטריצה המייצגת''' את T מבסיס E לבסיס F הינה המטריצה שעמודותיה הן הקואורדינטות לפי הבסיס F של התמונות של איברי הבסיס E. מסמנים |
| שורה 16: | שורה 16: | ||
\end{pmatrix} </math> | \end{pmatrix} </math> | ||
| + | |||
| + | '''הערה''' : המטריצה <math>[T]^E_F</math> היא המטריצה היחידה המקיימת את הטענה הבאה | ||
לכל וקטור <math>v\in V</math> מתקיים ש <math>[T]^E_F[v]_E=[Tv]_F</math> | לכל וקטור <math>v\in V</math> מתקיים ש <math>[T]^E_F[v]_E=[Tv]_F</math> | ||
| − | '''הערה | + | '''הערה''': שימו לב שמטריצת מעבר <math>[I]_B^{B'}</math> היא מקרה פרטי של מטריצה מייצגת. היא מייצגת את העתקת הזהות (ומכאן הסימון) <math>I:V\to V</math> |
| + | כאשר <math>B,B'</math> שני בסיסים של המרחב. | ||
| − | ===אלגוריתם למציאת מטריצה המייצגת את | + | |
| + | |||
| + | |||
| + | === דוגמא === | ||
| + | דוגמא: <math>V=\mathbb{R}_{2}[x],\,W=\mathbb{R}^{2}</math>. | ||
| + | ויהיו | ||
| + | <math> | ||
| + | E=\{1,x,x^{2}\},F=\{\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{array}\right)\}</math> | ||
| + | בסיסים בהתאמה | ||
| + | |||
| + | נגדיר <math>T:V\to W</math> ה"ל בעזרת משפט ההגדרה | ||
| + | <math>T(a+bx+cx^{2})=\left(\begin{array}{c} | ||
| + | b+c\\ | ||
| + | a | ||
| + | \end{array}\right)</math> | ||
| + | . | ||
| + | |||
| + | מצא את <math>[T]_{F}^{E}</math> | ||
| + | |||
| + | |||
| + | '''פתרון:''' | ||
| + | <math>T(1)=\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{array}\right)=0\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)+(1)\cdot\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{array}\right)</math> | ||
| + | ולכן | ||
| + | <math>[T(1)]_{F}=\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | |||
| + | <math>T(x)=\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)=1\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)+0\cdot\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{array}\right)</math> | ||
| + | ולכן | ||
| + | <math>[T(x)]_{F}=\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | |||
| + | <math>T(x^{2})=\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)=1\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)+0\cdot\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | 1 | ||
| + | \end{array}\right)</math> | ||
| + | ולכן | ||
| + | <math>[T(x^{2})]_{F}=\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | |||
| + | ולכן, בסך הכל נקבל | ||
| + | <math>[T]_{F}^{E}=\left(\begin{array}{ccc} | ||
| + | 0 & 1 & 1\\ | ||
| + | 1 & 0 & 0 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | '''הערה:''' שימו לב, כפי שראינו בתרגיל זה, שאם ניקח את הוקטורים <math>Tv_1,...,Tv_n</math> ונשים אותם באופן נאיבי בעמודות מטריצה נקבל <math>[T]^E_S</math> (כאשר S הוא הבסיס הסטנדרטי) | ||
| + | |||
| + | === תרגיל (6.12)=== | ||
| + | |||
| + | תהי <math>T:\mathbb{R}^2\rightarrow \mathbb{R}^2</math> העתקה של שיקוף ביחס לציר x. מצא בסיס סדור B ל <math>\mathbb{R}^2</math> עבורו <math>[T]_B=\begin{pmatrix} -1 & 2 \\ 0 & 1 \end{pmatrix}</math> | ||
| + | |||
| + | '''פתרון.''' | ||
| + | |||
| + | בסיס סדור יכיל שני וקטורים <math>v_1=(a,b),v_2=(c,d)</math>. לפי הנתונים <math>T(a,b)=(a,-b)</math> וגם <math>T(c,d)=(c,-d)</math>. | ||
| + | |||
| + | עמודות המטריצה המייצגת הינן הקואורדינטות של התמונות של איברי הבסיס, לפי הבסיס. לכן | ||
| + | |||
| + | <math>(a,-b)=T(a,b)=(-1)\cdot (a,b) + 0 \cdot (c,d)</math> | ||
| + | |||
| + | <math>(c,-d)=T(c,d)=2\cdot (a,b) + 1 \cdot (c,d)</math> | ||
| + | |||
| + | ביחד קיבלנו 4 משוואות: | ||
| + | |||
| + | <math>a=-a \Rightarrow a=0</math> | ||
| + | |||
| + | <math>-b=-b</math> | ||
| + | |||
| + | <math>c=2a+c=c</math> | ||
| + | |||
| + | <math>-d = 2b+d \Rightarrow d=-b</math> | ||
| + | |||
| + | לכן, עלינו לבחור <math>b,c,d</math> שיקיימו את המשוואות לעיל '''וגם''' יתקיים שהוקטורים <math>(a,b),(c,d)</math> בת"ל. | ||
| + | |||
| + | לכן b אינו אפס, וגם c אינו אפס. d חייב להיות -b. | ||
| + | |||
| + | ניקח <math>(0,1),(1,-1)</math> ואכן תנאי השאלה מתקיימים. | ||
| + | |||
| + | === תרגיל === | ||
| + | יהיו <math>V_1, V_2, V_3</math> מרחבים וקטורים עם בסיסים <math>B_1, B_2, B_3</math>בהתאמה. | ||
| + | יהיו <math>T:V_1\to V_2 S:V_2\to V_3</math> שתי ה"ל אזי מתקיים | ||
| + | <math>[S\circ T]^{B_1}_{B_3}=[S]^{B_2}_{B_3}\cdot[T]^{B_1}_{B_2}</math> | ||
| + | |||
| + | '''הוכחה''' מ"ל כי לכל <math>v\in V_1 </math> מתקיים <math>[S]^{B_2}_{B_3}\cdot[T]^{B_1}_{B_2}[v]_{B_1} =[(S\circ T)(v)]_{B_3} </math> (כי המטריצה המייצגת היא היחידה המקיימת את התנאי הזה) | ||
| + | |||
| + | ואכן, לפי הגדרת מטריצה מייצגת נקבל כי | ||
| + | |||
| + | <math> | ||
| + | [S]^{B_2}_{B_3}\cdot[T]^{B_1}_{B_2}[v]_{B_1} = | ||
| + | |||
| + | [S]^{B_2}_{B_3}\cdot [Tv]_{B_2}= | ||
| + | [S(T(v))]_{B_3} = | ||
| + | |||
| + | [(S\circ T)(v)]_{B_3} </math> | ||
| + | |||
| + | ==== מסקנה ==== | ||
| + | יהי <math>V</math> מ"ו, יהיו <math>B,B'</math> שני בסיסים שלו. אזי מטריצת המעבר <math>[I]_B^{B'}</math> הפיכה ומתקיים <math>([I]_B^{B'})^{-1} =[I]_{B'}^{B} </math> (כלומר ההופכית היא מטריצת המעבר "בכיוון ההפוך") | ||
| + | |||
| + | הוכחה: ישירות מתרגיל הקודם, <math>[I]_B^{B'}\cdot [I]_{B'}^{B} =[I]_{B}^{B} =I </math> | ||
| + | |||
| + | ===תרגיל=== | ||
| + | יהי <math>V</math> מ"ו, <math>B,C</math> בסיסים, <math>T:V\to V</math> הע"ל. הוכיחו או הפריכו: <math>([T]_B^C)^{-1}=[T]_C^B</math>. | ||
| + | |||
| + | ====פתרון==== | ||
| + | ממש לא. ראשית, מי אמר שמטריצה שמייצגת העתקה בכלל הפיכה? ושנית, כדאי להבין מה כן נותן הכפל בין המטריצות הללו: לפי הגדרת ההרכבה נקבל: <math>[T]_B^C\cdot [T]_C^B=[T^2]_B</math>, ואכן: <math>[T]_B^C\cdot [T]_C^B[v]_B=[T]_B^C[Tv]_C=[T^2v]_B</math>. | ||
| + | |||
| + | === תרגיל === | ||
| + | <math>V=\mathbb{R}_{2}[x],\,W=\mathbb{R}^{2}</math>. ויהיו | ||
| + | <math>E=\{-1,2+x,3+x+x^{2}\},F=\{\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right),\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 1 | ||
| + | \end{array}\right)\}</math> | ||
| + | בסיסים בהתאמה | ||
| + | |||
| + | נגדיר <math>T:V\to W</math> | ||
| + | ה"ל באופן הבא (בעזרת משפט ההגדרה) | ||
| + | <math>T(a+bx+cx^{2})=\left(\begin{array}{c} | ||
| + | b+c\\ | ||
| + | a | ||
| + | \end{array}\right)</math> | ||
| + | . | ||
| + | מצא את <math>[T]_{F}^{E}</math> | ||
| + | |||
| + | |||
| + | '''פתרון:''' | ||
| + | <math>T(-1)=\left(\begin{array}{c} | ||
| + | 0\\ | ||
| + | -1 | ||
| + | \end{array}\right)=1\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)+(-1)\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 1 | ||
| + | \end{array}\right)</math> | ||
| + | ולכן | ||
| + | <math>[T(-1)]_{F}=\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | -1 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | |||
| + | <math>T(2+x)=\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 2 | ||
| + | \end{array}\right)=-1\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)+2\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 1 | ||
| + | \end{array}\right)</math> | ||
| + | ולכן | ||
| + | <math>[T(2+x)]_{F}=\left(\begin{array}{c} | ||
| + | -1\\ | ||
| + | 2 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | |||
| + | <math>T(3+x+x^{2})=\left(\begin{array}{c} | ||
| + | 2\\ | ||
| + | 3 | ||
| + | \end{array}\right)=-1\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 0 | ||
| + | \end{array}\right)+3\cdot\left(\begin{array}{c} | ||
| + | 1\\ | ||
| + | 1 | ||
| + | \end{array}\right)</math> | ||
| + | ולכן | ||
| + | <math>[T(3+x+x^{2})]_{F}=\left(\begin{array}{c} | ||
| + | -1\\ | ||
| + | 3 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | ולכן, בסופו של דבר, | ||
| + | <math>[T]_{F}^{E}=\left(\begin{array}{ccc} | ||
| + | 1 & -1 & -1\\ | ||
| + | -1 & 2 & 3 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | ==== דרך פתרון נוספת ==== | ||
| + | לא תמיד קל להביע וקטור כצ"ל של האחרים (בתרגיל הזה זה פשוט נתון..). הנה עוד דרך, נמצא את המטריצות <math>[I]_F^S,[T]_S^E</math>, כאשר <math>S</math> הוא בסיס סטנדרטי (שימו לב שיש פה שניים) ואז נכפול בניהם, ולפי הערה ממקודם נקבל <math> [I]_F^S \cdot [T]_S^E = [T]_F^E</math>. | ||
| + | |||
| + | המטריצה <math>[T]_S^E</math> קלה לחישוב כי חישוב של צ"ל לפי <math>S</math> זה קל | ||
| + | |||
| + | <math> | ||
| + | [T]_S^E = | ||
| + | \begin{pmatrix} | ||
| + | 0 & 1 & 2 \\ | ||
| + | -1 & 2 & 3 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | כעת בשביל לחשב את <math>[I]_F^S</math> יש לחשב את ההופכית של | ||
| + | <math>[I]_S^F = | ||
| + | \begin{pmatrix} | ||
| + | 1 & 1 \\ | ||
| + | 0 & 1 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | שהיא (זה מטריצה אלמנטרית ולכן קל להפוך..) | ||
| + | |||
| + | <math>[I]_F^S = | ||
| + | \begin{pmatrix} | ||
| + | 1 & -1 \\ | ||
| + | 0 & 1 | ||
| + | \end{pmatrix} | ||
| + | |||
| + | </math> | ||
| + | |||
| + | נכפיל את המטריצות ואכן נקבל | ||
| + | |||
| + | <math> | ||
| + | |||
| + | [T]_F^E= [I]_F^S [T]_S^E = | ||
| + | \begin{pmatrix} | ||
| + | 1 & -1 \\ | ||
| + | 0 & 1 | ||
| + | \end{pmatrix} | ||
| + | \cdot | ||
| + | \begin{pmatrix} | ||
| + | 0 & 1 & 2 \\ | ||
| + | -1 & 2 & 3 | ||
| + | \end{pmatrix} | ||
| + | |||
| + | |||
| + | = | ||
| + | |||
| + | \begin{pmatrix} | ||
| + | 1 & -1 & -1 \\ | ||
| + | -1 & 2 & 3 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | === תרגיל חשוב!=== | ||
| + | תהא <math>T:\mathbb{R}^{2\times2}\to\mathbb{R}^{2\times2}</math> המקיימת כי | ||
| + | <math>T\left(\begin{array}{cc} | ||
| + | 1 & 0\\ | ||
| + | 0 & 0 | ||
| + | \end{array}\right),T\left(\begin{array}{cc} | ||
| + | 0 & 1\\ | ||
| + | 0 & 0 | ||
| + | \end{array}\right),T\left(\begin{array}{cc} | ||
| + | 0 & 0\\ | ||
| + | 1 & 0 | ||
| + | \end{array}\right)\in\text{span}\left\{ \left(\begin{array}{cc} | ||
| + | 1 & 1\\ | ||
| + | 0 & 0 | ||
| + | \end{array}\right),\left(\begin{array}{cc} | ||
| + | 1 & 0\\ | ||
| + | 1 & 0 | ||
| + | \end{array}\right)\right\}</math> | ||
| + | ובנוסף נתונה מטריצה מייצגת שלה | ||
| + | <math>[T]_{C}^{B}=\left(\begin{array}{cccc} | ||
| + | 1 & 2 & 3 & 4\\ | ||
| + | 0 & 5 & 6 & 7\\ | ||
| + | 0 & 0 & 8 & x\\ | ||
| + | 0 & 0 & 4 & x | ||
| + | \end{array}\right)</math> | ||
| + | (עבור איזה שהן בסיסים <math>B,C</math>) מצאו את <math>x</math>. | ||
| + | |||
| + | *קבעו איזה איברים של השורה האחרונה של <math>[T^{10}]_{S}^{S}</math> הם בודאות ששוים לאפס .(כאשר S הוא הבסיס הסטנדרטי). | ||
| + | |||
| + | *הוכיחו שקיים בסיס <math>D</math> ל <math>\mathbb{R}^{2\times2}</math> כך המטריצה המייצגת מהצורה | ||
| + | <math>[T]_{D}^{D}=\left(\begin{array}{cccc} | ||
| + | 0 & * & * & *\\ | ||
| + | 0 & * & * & *\\ | ||
| + | 0 & * & * & *\\ | ||
| + | 0 & * & * & * | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | ויש בנוסף שורת אפסים | ||
| + | |||
| + | === תרגיל חשוב! === | ||
| + | יהא <math>V=\mathbb{R}_{2}[x]</math> ושני בסיסים <math>B=\left\{ 2+x,3-x+x^{2},-2+4x-x^{2}\right\} ,C=\left\{ 1+x+x^{2},2+2x,x+2x^{2}\right\}</math> שני בסיסים של <math>V</math>. בנוסף, נסמן <math>S=\left\{ 1,x,x^{2}\right\}</math> את הבסיס הסטנדרטי של <math>V</math>. | ||
| + | |||
| + | *מצאו את מטריצות המעבר <math>[I]_{C}^{B},[I]_{S}^{B},[I]_{C}^{S}</math> ומצאו את <math>[I]_{B}^{C}</math> | ||
| + | |||
| + | * נגדיר <math>T:V\to V</math> ע"י הכלל <math>T(p(x))=p(x+1)</math>. מצאו את המטריצה <math>[T]_{C}^{B},[T]_{C}^{C}</math>. | ||
| + | |||
| + | |||
| + | |||
| + | ** הוכיחו/הפריכו: קיימת <math>\hat{T}:\mathbb{R}_{2}[x]\to\mathbb{R}_{2}[x]</math> כך ש <math>[\hat{T}\circ T]_{C}^{B} =\left(\begin{array}{ccc} | ||
| + | 3 & 0 & 0\\ | ||
| + | 0 & 0 & 0\\ | ||
| + | 0 & 0 & 0 | ||
| + | \end{array}\right)</math> | ||
| + | וגם<math> | ||
| + | [T\circ\hat{T}]_{B}^{C} =\left(\begin{array}{ccc} | ||
| + | 0 & 0 & 0\\ | ||
| + | 0 & 0 & 0\\ | ||
| + | 0 & 0 & 0 | ||
| + | \end{array}\right) | ||
| + | </math> | ||
| + | **הוכיחו/הפריכו: קיימת <math>\hat{T}:\mathbb{R}_{2}[x]\to\mathbb{R}_{2}[x]</math> כך ש | ||
| + | <math>[\hat{T}\circ T]_{B}^{B} =\left(\begin{array}{ccc} | ||
| + | 1 & 0 & 0\\ | ||
| + | 0 & 2 & 0\\ | ||
| + | 0 & 0 & 0 | ||
| + | \end{array}\right)</math> | ||
| + | וגם | ||
| + | <math>[T\circ\hat{T}]_{S}^{C} =\left(\begin{array}{ccc} | ||
| + | 1 & 0 & 0\\ | ||
| + | 0 & 2 & 0\\ | ||
| + | 0 & 0 & 3 | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | ** מצאו לאילו ערכי <math>a</math> קיימת <math>\hat{T}:\mathbb{R}_{2}[x]\to\mathbb{R}_{2}[x]</math> כך ש | ||
| + | <math>[\hat{T}\circ T]_{C}^{B} =\left(\begin{array}{ccc} | ||
| + | 1 & 2 & 3\\ | ||
| + | 4 & 5 & 6\\ | ||
| + | 7 & 8 & a | ||
| + | \end{array}\right)</math> | ||
| + | |||
| + | ===אלגוריתם למציאת מטריצה המייצגת את ההעתקה בין בסיסים כלשהם=== | ||
| + | |||
| + | הנה אלגוריתם שמכליל את הדוגמא הקודמת. | ||
יהיו מ"ו V,W והעתקה T בינהם ובסיסים E,F בדיוק כמו בהגדרה לעיל. אזי: | יהיו מ"ו V,W והעתקה T בינהם ובסיסים E,F בדיוק כמו בהגדרה לעיל. אזי: | ||
| − | # מצא את | + | # מצא את מטריצת המעבר <math>[I]^F_S</math> (קל, לשים את הקואורדינטות לפי הבסיס הסטנדרטי של איברי F בעמודות) |
# הפוך אותה על מנת לקבל את <math>[I]^S_F</math> | # הפוך אותה על מנת לקבל את <math>[I]^S_F</math> | ||
# הפעל את ההעתקה T על איברי הבסיס E לקבל <math>Tv_1,...,Tv_n</math> | # הפעל את ההעתקה T על איברי הבסיס E לקבל <math>Tv_1,...,Tv_n</math> | ||
| שורה 32: | שורה 394: | ||
===אלגוריתם למציאת העתקה מפורשת לפי תמונות איברי הבסיס בלבד=== | ===אלגוריתם למציאת העתקה מפורשת לפי תמונות איברי הבסיס בלבד=== | ||
| − | תהי T העתקה לינארית הנתונה על ידי התמונות של איברי בסיס <math> | + | תהי T העתקה לינארית הנתונה על ידי התמונות של איברי בסיס <math>E=\{v_1,...,v_n\}</math>. רוצים למצוא את <math>Tv</math> עבור <math>v\in V</math> וקטור כלשהו. |
#נבצע את האלגוריתם לעיל על מנת למצוא את <math>[T]^E_S</math>. | #נבצע את האלגוריתם לעיל על מנת למצוא את <math>[T]^E_S</math>. | ||
#נכפול במטריצת המעבר על מנת לקבל <math>[T]=[T]^S_S=[T]^E_S[I]^S_E</math> | #נכפול במטריצת המעבר על מנת לקבל <math>[T]=[T]^S_S=[T]^E_S[I]^S_E</math> | ||
| − | #<math>[T][v]=[Tv]</math> מכיוון שכל | + | #<math>[T][v]=[Tv]</math> מכיוון שכל אלה בבסיס הסטנדרטי, נכפול בוקטור כללי מהמרחב על מנת למצוא לאן הוא נשלח במפורש. |
===דוגמא=== | ===דוגמא=== | ||
| − | '''תרגיל.''' יהיו <math>V=span\{v_1=(1,0,-1,1),v_2=(-2,1,2,0),v_3=(0,-1,0,1)\}</math> ו <math>W=\mathbb{R}_3[x]</math> מ"ו. תהי העתקה T מV | + | '''תרגיל.''' יהיו <math>V=span\{v_1=(1,0,-1,1),v_2=(-2,1,2,0),v_3=(0,-1,0,1)\}</math> ו <math>W=\mathbb{R}_3[x]</math> מ"ו. תהי העתקה T מV לW המקיימת <math>\forall i:Tv_i=w_i</math> כאשר |
<math>w_1=1+x</math> | <math>w_1=1+x</math> | ||
| שורה 50: | שורה 412: | ||
| − | + | ====פתרון==== | |
| − | דבר ראשון נמצא את המטריצה המייצגת | + | דבר ראשון נמצא את המטריצה המייצגת מ <math>B=\{v_1,v_2,v_3\}</math> לבסיס הסטדנרטי של הפולינומים S. נשים את התמונות בעמודות |
<math>[T]^B_S =\begin{pmatrix} | <math>[T]^B_S =\begin{pmatrix} | ||
| שורה 84: | שורה 446: | ||
</math> | </math> | ||
| − | כעת נמצא את מטריצת המעבר. שימו לב שאנו עוסקים במקרה מיוחד. המרחב שלנו אינו מרחב מוכר, ואנו צריכים למצוא לו בסיס סטנרטי על מנת לקחת את הקואורדינטות של איברי הבסיס הנתון לפי אותו בסיס סטנדרטי שנמציא. | + | כעת נמצא את מטריצת המעבר. שימו לב שאנו עוסקים במקרה מיוחד. המרחב שלנו אינו מרחב מוכר, ואנו צריכים למצוא לו בסיס סטנרטי על מנת לקחת את הקואורדינטות של איברי הבסיס הנתון לפי אותו בסיס סטנדרטי שנמציא. נדרג מטריצה ששורתיה עם הוקטורים הנ"ל. כיוון שמרחב השורות לא משתנה נקבל בסיס אחר יותר נח. |
| − | + | <math> | |
| + | \begin{pmatrix} | ||
| + | 1 & 0 & -1 &1 \\ | ||
| + | -2 & 1 & 2 & 0 \\ | ||
| + | 0 &-1 & 0 &1 | ||
| + | \end{pmatrix} | ||
| + | \to | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & -1 &1 \\ | ||
| + | 0 & 1 & 0 & 2 \\ | ||
| + | 0 &-1 & 0 &1 | ||
| + | \end{pmatrix} | ||
| + | \to | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & -1 &1 \\ | ||
| + | 0 & 1 & 0 & 2 \\ | ||
| + | 0 &0 & 0 &3 | ||
| + | \end{pmatrix} | ||
| + | \to | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & -1 &0 \\ | ||
| + | 0 & 1 & 0 & 0 \\ | ||
| + | 0 &0 & 0 &1 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | ולכן בסיס אלטרנטיבי למרחב שלנו הוא | ||
| + | <math>S_V=\{(-1,0,1,0),(0,1,0,0),(0,0,0,1)\}</math>. מדוע הוא סטנדרטי? קל מאד לראות שלכל וקטור במרחב <math>[(-x,y,x,z)]_{S_V}=(x,y,z)</math>. | ||
| שורה 188: | שורה 576: | ||
<math>T(-a,b,a,d)=b+d +(b+d)x + \frac{1}{3}(a+b+d)x^2+ \frac{1}{3}(a+b+d)x^3</math> | <math>T(-a,b,a,d)=b+d +(b+d)x + \frac{1}{3}(a+b+d)x^2+ \frac{1}{3}(a+b+d)x^3</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===מחלקת שקילות של מטריצות המייצגות העתקה=== | ===מחלקת שקילות של מטריצות המייצגות העתקה=== | ||
| − | + | טענה: יהא <math>V</math> מ"ו מימד סופי <math>B=\{v_1,\dots v_n\}</math> בסיס. תהא <math>A\in \mathbb{F}^{n\times n}</math> הפיכה. | |
| − | + | אזי קיים <math>B'</math> בסיס אחר כך ש <math>[I]^{B'}_B= A</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | (במילים: המטריצה A היא מטריצת מעבר מאיזה שהוא בסיס אחר לבסיס הנתון) | ||
| − | ''' | + | הוכחה: נגדיר <math>B'=\{v'_1,\dots v'_n\}</math> ע"י <math>v'_j=\sum_{i=1}^n A_{i,j}\cdot v_i </math>. |
| + | לפי הגדרה מתקיים כי <math>[I]^{B'}_B= A</math>. נותר להוכיח כי אכן <math>B'</math> בסיס. | ||
| + | כיוון ש <math>|B'|=n</math> אזי אם נוכיח כי <math>B'</math> בת"ל אזי הוא בסיס לפי השלישי חינם. | ||
| + | נוכיח כי <math>B'</math> בת"ל | ||
| − | + | נניח כי <math>\sum_{j=1}^n \alpha_j v'_j =0</math>. צ"ל כי <math>\forall i \; \alpha_i =0</math> | |
| − | + | <math>0=\sum_{j=1}^n \alpha_j v'_j =\sum_{j=1}^n \alpha_j \sum_{i=1}^n A_{i,j}\cdot v_i =\sum_{i=1}^n \big( \sum_{j=1}^n \alpha_j A_{i,j} \big) \cdot v_i </math> | |
| − | <math> | + | |
| − | + | כיוון ש <math>B</math> בת"ל נקבל כי לכל <math>i</math> מתקיים כי <math> \sum_{j=1}^n \alpha_j A_{i,j} =0</math> | |
| − | + | ||
| − | + | אבל זה בדיוק הקורדינאטה ה <math>i</math> - ית של הכפל <math>(\alpha_1,\dots \alpha_n)\cdot A </math> | |
| − | + | ולכן <math>(\alpha_1,\dots \alpha_n)\cdot A =(0,0,\dots ,0) </math> ע"י הכפלה מימין ב <math>A^{-1}</math> נקבל את הדרוש. | |
| − | + | בניה: | |
| − | + | על המטריצות הריבועיות <math>\mathbb{F}^{n\times n}</math> נגדיר יחס שקילות באופן הבא: | |
| − | + | <math>A\approx B</math> אם קיימת מטריצה הפיכה <math>P</math> כך ש <math>A=P^{-1}BP</math>. | |
| − | + | ||
| − | + | ||
| + | יחס זה נקרא "הצמדה". | ||
| − | + | הוכיחו כי זהו אכן יחס שקילות. | |
| − | + | '''טענה מרכזית''' | |
| − | + | יהא <math>V</math> מ"ו מימד סופי <math>n</math>. תהא <math>T:V\to V</math> ה"ל. | |
| + | ונשתמש בסימון <math>\approx</math> כיחס ההצמדה על המטריצות <math>\mathbb{F}^{n\times n}</math> שהגדרנו לעיל. | ||
| + | מתקיים כי | ||
| − | + | 1. <math>[T]_B \approx [T]_{B'}</math> עבור כל 2 בסיסים <math>B,B'</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ' | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | 2. אם <math>[T]_B \approx A</math> עבור <math>B </math> בסיס כל שהוא אזי קיים בסיס <math>B'</math> | |
| + | כך ש <math>[T]_{B'}=A</math> | ||
| + | במילים- המטריצה המייצגת של <math>T</math> יחידה עד כדי הצמדה. | ||
| − | + | כלומר אם נייצג את <math>T</math> ע"י 2 בסיסים נקבל מטריצות צמודות ומאידך גיסא אם יש מטריצה <math>A</math> הצמודה לאיזה שהוא מטריצה מייצגת של <math>T</math> אז גם המטריצה <math>A</math> מייצגת את <math>T</math> | |
| + | הוכחה: | ||
| − | + | 1. מתקיים בגלל השיוויון <math>[T]^B_B=[I]^{B'}_B[T]^{B'}_{B'}[I]^B_{B'}</math> ומתקיים כי <math>[I]^{B'}_B</math> הופכית של <math>[I]^B_{B'}</math> | |
| + | 2. נתון כי קיימת מטריצה הפיכה <math>P</math> כך ש <math>P^{-1}[T]_BP = A</math> מהטענה שהוכחנו לעיל קיים בסיס <math>B'</math> כך ש <math>[I]^{B'}_B= P</math> ואז <math>A=P^{-1}[T]_BP = [I]^B_{B'}[T]_B[I]^{B'}_B=[T]^{B'}_{B'}</math> | ||
| + | כלומר <math>A</math> אכן מייצגת את <math>T</math> לפי הבסיס <math>B'</math>. | ||
| − | |||
| − | <math> | + | הגדרה: |
| + | יהא <math>V</math> מ"ו מימד סופי <math>n</math>. תהא <math>T:V\to V</math> ה"ל. | ||
| + | אזי העקבה של <math>T</math> מוגדרת להיות | ||
| + | <math>trace(T)=trace([T]_B)</math> כאשר <math>B</math> בסיס כלשהוא. (או בקיצור <math>tr([T]_B)</math>) | ||
| − | + | הערה: ההגדרה לא תלויה בבחירת הבסיס. כלומר עבור 2 בסיסים <math>B,B'</math> | |
| + | מתקיים כי <math>trace([T]_{B'})=trace([T]_B)</math>. | ||
| + | למה? לפי הטענה המרכזית קיימת <math>P</math> הפיכה כך ש | ||
| + | <math>[T]_B=P^{-1}[T]_{B'}P</math> | ||
| + | ואז מתקיים <math>tr([T]_B)=tr(P^{-1}[T]_{B'}P)=tr(PP^{-1}[T]_{B'})=tr([T]_{B'})</math> | ||
| − | + | המעבר באמצע נובע מהעובדה כי לכל 2 מטריצות <math>A,B</math> מתקיים כי <math>tr(AB)=tr(BA)</math> | |
גרסה אחרונה מ־13:46, 11 באוגוסט 2020
תוכן עניינים
מטריצות מייצגות
הגדרה. תהי 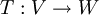 העתקה לינארית, ויהיו
העתקה לינארית, ויהיו 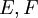 בסיסים ל
בסיסים ל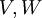 בהתאמה. נסמן
בהתאמה. נסמן 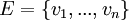 . אזי המטריצה המייצגת את T מבסיס E לבסיס F הינה המטריצה שעמודותיה הן הקואורדינטות לפי הבסיס F של התמונות של איברי הבסיס E. מסמנים
. אזי המטריצה המייצגת את T מבסיס E לבסיס F הינה המטריצה שעמודותיה הן הקואורדינטות לפי הבסיס F של התמונות של איברי הבסיס E. מסמנים
![[T]^E_F =\begin{pmatrix}
| & | & & | \\
\big[Tv_1]_F & [Tv_2]_F &\cdots &[Tv_n]_F \\
| & | & & | \\
\end{pmatrix}](/images/math/4/9/e/49e2f9dc3d8c41267aacd3680fa20858.png)
הערה : המטריצה ![[T]^E_F](/images/math/d/b/e/dbe7dc25144f974a7ba5c280de7854ba.png) היא המטריצה היחידה המקיימת את הטענה הבאה
היא המטריצה היחידה המקיימת את הטענה הבאה
לכל וקטור 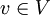 מתקיים ש
מתקיים ש ![[T]^E_F[v]_E=[Tv]_F](/images/math/8/f/e/8fe37ba3f4825212a8b25b6ea6cccb56.png)
הערה: שימו לב שמטריצת מעבר ![[I]_B^{B'}](/images/math/c/6/c/c6c3e3bb9bd1842dec9878a5848f742a.png) היא מקרה פרטי של מטריצה מייצגת. היא מייצגת את העתקת הזהות (ומכאן הסימון)
היא מקרה פרטי של מטריצה מייצגת. היא מייצגת את העתקת הזהות (ומכאן הסימון) 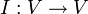 כאשר
כאשר 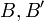 שני בסיסים של המרחב.
שני בסיסים של המרחב.
דוגמא
דוגמא: ![V=\mathbb{R}_{2}[x],\,W=\mathbb{R}^{2}](/images/math/2/c/1/2c10a1615373fc1ae565132222c34e7d.png) .
ויהיו
.
ויהיו
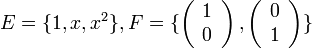 בסיסים בהתאמה
בסיסים בהתאמה
נגדיר 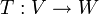 ה"ל בעזרת משפט ההגדרה
ה"ל בעזרת משפט ההגדרה
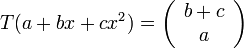 .
.
מצא את ![[T]_{F}^{E}](/images/math/0/4/8/04889bf5bccf0334ce2b7ea97d2f1e76.png)
פתרון:
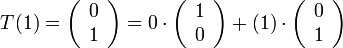 ולכן
ולכן
![[T(1)]_{F}=\left(\begin{array}{c}
0\\
1
\end{array}\right)](/images/math/0/2/6/026792376b975dcc1c3b8dab674d2660.png)
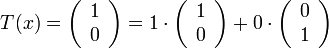 ולכן
ולכן
![[T(x)]_{F}=\left(\begin{array}{c}
1\\
0
\end{array}\right)](/images/math/5/e/7/5e7d29485b1655415c17457a320222b0.png)
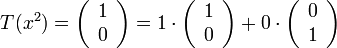 ולכן
ולכן
![[T(x^{2})]_{F}=\left(\begin{array}{c}
1\\
0
\end{array}\right)](/images/math/f/7/9/f79ce9932a5aeb98495a742a1bab335f.png)
ולכן, בסך הכל נקבל
![[T]_{F}^{E}=\left(\begin{array}{ccc}
0 & 1 & 1\\
1 & 0 & 0
\end{array}\right)](/images/math/9/7/1/9710f16c78c9e65aa547a385ec02e823.png)
הערה: שימו לב, כפי שראינו בתרגיל זה, שאם ניקח את הוקטורים 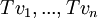 ונשים אותם באופן נאיבי בעמודות מטריצה נקבל
ונשים אותם באופן נאיבי בעמודות מטריצה נקבל ![[T]^E_S](/images/math/5/e/8/5e82090d1f89376b1881037a7b72f065.png) (כאשר S הוא הבסיס הסטנדרטי)
(כאשר S הוא הבסיס הסטנדרטי)
תרגיל (6.12)
תהי 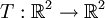 העתקה של שיקוף ביחס לציר x. מצא בסיס סדור B ל
העתקה של שיקוף ביחס לציר x. מצא בסיס סדור B ל 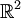 עבורו
עבורו ![[T]_B=\begin{pmatrix} -1 & 2 \\ 0 & 1 \end{pmatrix}](/images/math/2/4/e/24edf4a4c11bcd1304d0bb4c97551cbe.png)
פתרון.
בסיס סדור יכיל שני וקטורים 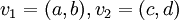 . לפי הנתונים
. לפי הנתונים 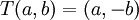 וגם
וגם 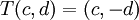 .
.
עמודות המטריצה המייצגת הינן הקואורדינטות של התמונות של איברי הבסיס, לפי הבסיס. לכן
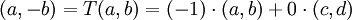
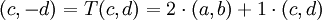
ביחד קיבלנו 4 משוואות:
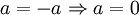
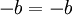
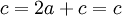
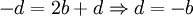
לכן, עלינו לבחור 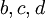 שיקיימו את המשוואות לעיל וגם יתקיים שהוקטורים
שיקיימו את המשוואות לעיל וגם יתקיים שהוקטורים 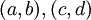 בת"ל.
בת"ל.
לכן b אינו אפס, וגם c אינו אפס. d חייב להיות -b.
ניקח 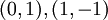 ואכן תנאי השאלה מתקיימים.
ואכן תנאי השאלה מתקיימים.
תרגיל
יהיו 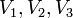 מרחבים וקטורים עם בסיסים
מרחבים וקטורים עם בסיסים 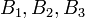 בהתאמה.
יהיו
בהתאמה.
יהיו 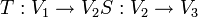 שתי ה"ל אזי מתקיים
שתי ה"ל אזי מתקיים
![[S\circ T]^{B_1}_{B_3}=[S]^{B_2}_{B_3}\cdot[T]^{B_1}_{B_2}](/images/math/c/f/1/cf1267ae1ce5d707a96a2a206e71de53.png)
הוכחה מ"ל כי לכל 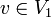 מתקיים
מתקיים ![[S]^{B_2}_{B_3}\cdot[T]^{B_1}_{B_2}[v]_{B_1} =[(S\circ T)(v)]_{B_3}](/images/math/3/b/5/3b5176d197adc4a820d8095229e8af26.png) (כי המטריצה המייצגת היא היחידה המקיימת את התנאי הזה)
(כי המטריצה המייצגת היא היחידה המקיימת את התנאי הזה)
ואכן, לפי הגדרת מטריצה מייצגת נקבל כי
![[S]^{B_2}_{B_3}\cdot[T]^{B_1}_{B_2}[v]_{B_1} =
[S]^{B_2}_{B_3}\cdot [Tv]_{B_2}=
[S(T(v))]_{B_3} =
[(S\circ T)(v)]_{B_3}](/images/math/5/9/8/598b80d885abaf02297185587762539a.png)
מסקנה
יהי  מ"ו, יהיו
מ"ו, יהיו 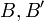 שני בסיסים שלו. אזי מטריצת המעבר
שני בסיסים שלו. אזי מטריצת המעבר ![[I]_B^{B'}](/images/math/c/6/c/c6c3e3bb9bd1842dec9878a5848f742a.png) הפיכה ומתקיים
הפיכה ומתקיים ![([I]_B^{B'})^{-1} =[I]_{B'}^{B}](/images/math/9/6/8/968e6d43293ed99ff8e1e6cad8576216.png) (כלומר ההופכית היא מטריצת המעבר "בכיוון ההפוך")
(כלומר ההופכית היא מטריצת המעבר "בכיוון ההפוך")
הוכחה: ישירות מתרגיל הקודם, ![[I]_B^{B'}\cdot [I]_{B'}^{B} =[I]_{B}^{B} =I](/images/math/e/2/4/e24d7bd8b37056ed574440499b1da68b.png)
תרגיל
יהי  מ"ו,
מ"ו, 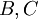 בסיסים,
בסיסים, 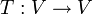 הע"ל. הוכיחו או הפריכו:
הע"ל. הוכיחו או הפריכו: ![([T]_B^C)^{-1}=[T]_C^B](/images/math/1/0/9/1094cc598deb7a0ff1bfe4d763006e09.png) .
.
פתרון
ממש לא. ראשית, מי אמר שמטריצה שמייצגת העתקה בכלל הפיכה? ושנית, כדאי להבין מה כן נותן הכפל בין המטריצות הללו: לפי הגדרת ההרכבה נקבל: ![[T]_B^C\cdot [T]_C^B=[T^2]_B](/images/math/a/4/6/a465e0cf9a14abc70cfa8f9d6e2e9aa7.png) , ואכן:
, ואכן: ![[T]_B^C\cdot [T]_C^B[v]_B=[T]_B^C[Tv]_C=[T^2v]_B](/images/math/7/7/3/773178f748c840ded6ceb1ba53c6de3e.png) .
.
תרגיל
![V=\mathbb{R}_{2}[x],\,W=\mathbb{R}^{2}](/images/math/2/c/1/2c10a1615373fc1ae565132222c34e7d.png) . ויהיו
. ויהיו
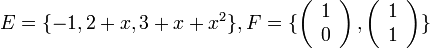 בסיסים בהתאמה
בסיסים בהתאמה
נגדיר 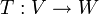 ה"ל באופן הבא (בעזרת משפט ההגדרה)
ה"ל באופן הבא (בעזרת משפט ההגדרה)
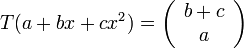 .
מצא את
.
מצא את ![[T]_{F}^{E}](/images/math/0/4/8/04889bf5bccf0334ce2b7ea97d2f1e76.png)
פתרון:
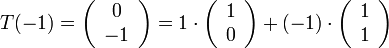 ולכן
ולכן
![[T(-1)]_{F}=\left(\begin{array}{c}
1\\
-1
\end{array}\right)](/images/math/7/3/e/73e4e38739da87c3261f27075db75339.png)
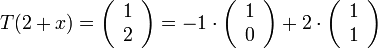 ולכן
ולכן
![[T(2+x)]_{F}=\left(\begin{array}{c}
-1\\
2
\end{array}\right)](/images/math/5/d/4/5d4296674431867541b55443bb004382.png)
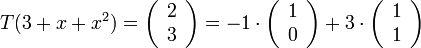 ולכן
ולכן
![[T(3+x+x^{2})]_{F}=\left(\begin{array}{c}
-1\\
3
\end{array}\right)](/images/math/1/e/e/1ee3ae5f767da29c81a8572324d5abc5.png)
ולכן, בסופו של דבר,
![[T]_{F}^{E}=\left(\begin{array}{ccc}
1 & -1 & -1\\
-1 & 2 & 3
\end{array}\right)](/images/math/0/f/3/0f34742d116711f11d35a4e29f1904a8.png)
דרך פתרון נוספת
לא תמיד קל להביע וקטור כצ"ל של האחרים (בתרגיל הזה זה פשוט נתון..). הנה עוד דרך, נמצא את המטריצות ![[I]_F^S,[T]_S^E](/images/math/6/6/5/665d6d18838f4c766c89726e413c9b7d.png) , כאשר
, כאשר 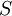 הוא בסיס סטנדרטי (שימו לב שיש פה שניים) ואז נכפול בניהם, ולפי הערה ממקודם נקבל
הוא בסיס סטנדרטי (שימו לב שיש פה שניים) ואז נכפול בניהם, ולפי הערה ממקודם נקבל ![[I]_F^S \cdot [T]_S^E = [T]_F^E](/images/math/e/8/2/e825d94eb6461def71cdc0cc8806629e.png) .
.
המטריצה ![[T]_S^E](/images/math/5/e/8/5e82090d1f89376b1881037a7b72f065.png) קלה לחישוב כי חישוב של צ"ל לפי
קלה לחישוב כי חישוב של צ"ל לפי 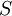 זה קל
זה קל
![[T]_S^E =
\begin{pmatrix}
0 & 1 & 2 \\
-1 & 2 & 3
\end{pmatrix}](/images/math/e/2/3/e23785267ceb75e6c67107d6eb48bb0d.png)
כעת בשביל לחשב את ![[I]_F^S](/images/math/f/f/4/ff48ee9930528f63e9a01fa9b5313b11.png) יש לחשב את ההופכית של
יש לחשב את ההופכית של
![[I]_S^F =
\begin{pmatrix}
1 & 1 \\
0 & 1
\end{pmatrix}](/images/math/f/4/d/f4dfaa0a9ffe416b54015aa500763e88.png)
שהיא (זה מטריצה אלמנטרית ולכן קל להפוך..)
![[I]_F^S =
\begin{pmatrix}
1 & -1 \\
0 & 1
\end{pmatrix}](/images/math/6/d/4/6d4c423fe95b5aaea838a7f68e6fbd66.png)
נכפיל את המטריצות ואכן נקבל
![[T]_F^E= [I]_F^S [T]_S^E =
\begin{pmatrix}
1 & -1 \\
0 & 1
\end{pmatrix}
\cdot
\begin{pmatrix}
0 & 1 & 2 \\
-1 & 2 & 3
\end{pmatrix}
=
\begin{pmatrix}
1 & -1 & -1 \\
-1 & 2 & 3
\end{pmatrix}](/images/math/8/6/9/869098689937d7df4617d7e2b3d81dc1.png)
תרגיל חשוב!
תהא 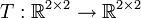 המקיימת כי
המקיימת כי
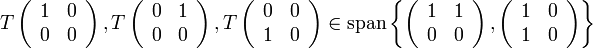 ובנוסף נתונה מטריצה מייצגת שלה
ובנוסף נתונה מטריצה מייצגת שלה
![[T]_{C}^{B}=\left(\begin{array}{cccc}
1 & 2 & 3 & 4\\
0 & 5 & 6 & 7\\
0 & 0 & 8 & x\\
0 & 0 & 4 & x
\end{array}\right)](/images/math/b/f/d/bfda22fc679d5394bceeb53525513fdc.png) (עבור איזה שהן בסיסים
(עבור איזה שהן בסיסים 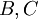 ) מצאו את
) מצאו את  .
.
- קבעו איזה איברים של השורה האחרונה של
![[T^{10}]_{S}^{S}](/images/math/f/d/7/fd7ffacc02c1107685bde6bcd1938927.png) הם בודאות ששוים לאפס .(כאשר S הוא הבסיס הסטנדרטי).
הם בודאות ששוים לאפס .(כאשר S הוא הבסיס הסטנדרטי).
- הוכיחו שקיים בסיס
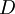 ל
ל 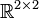 כך המטריצה המייצגת מהצורה
כך המטריצה המייצגת מהצורה
![[T]_{D}^{D}=\left(\begin{array}{cccc}
0 & * & * & *\\
0 & * & * & *\\
0 & * & * & *\\
0 & * & * & *
\end{array}\right)](/images/math/0/e/2/0e2787a7fda9ae2e66dbea8a6735cdea.png)
ויש בנוסף שורת אפסים
תרגיל חשוב!
יהא ![V=\mathbb{R}_{2}[x]](/images/math/f/7/3/f73cc35842c78e71bd2b26bb136b5c6a.png) ושני בסיסים
ושני בסיסים 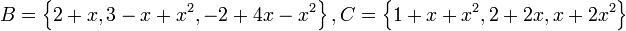 שני בסיסים של
שני בסיסים של  . בנוסף, נסמן
. בנוסף, נסמן 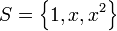 את הבסיס הסטנדרטי של
את הבסיס הסטנדרטי של  .
.
- מצאו את מטריצות המעבר
![[I]_{C}^{B},[I]_{S}^{B},[I]_{C}^{S}](/images/math/8/0/7/8071b5263183a65adc30b1431158e20b.png) ומצאו את
ומצאו את ![[I]_{B}^{C}](/images/math/f/d/7/fd7f519aca0e09b5c548913f7ba6918b.png)
- נגדיר
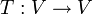 ע"י הכלל
ע"י הכלל 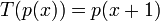 . מצאו את המטריצה
. מצאו את המטריצה ![[T]_{C}^{B},[T]_{C}^{C}](/images/math/f/6/3/f630bdbb9d716d29962a53ffe44c1747.png) .
.
- הוכיחו/הפריכו: קיימת
![\hat{T}:\mathbb{R}_{2}[x]\to\mathbb{R}_{2}[x]](/images/math/4/7/b/47be5dfe9a37bacf9baf8b4a0b07907b.png) כך ש
כך ש ![[\hat{T}\circ T]_{C}^{B} =\left(\begin{array}{ccc}
3 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{array}\right)](/images/math/7/b/d/7bd909902570496b61e90ddcd4286040.png)
- הוכיחו/הפריכו: קיימת
וגם![[T\circ\hat{T}]_{B}^{C} =\left(\begin{array}{ccc}
0 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{array}\right)](/images/math/9/7/8/978743bab6315e676d811718bba1666a.png)
- הוכיחו/הפריכו: קיימת
![\hat{T}:\mathbb{R}_{2}[x]\to\mathbb{R}_{2}[x]](/images/math/4/7/b/47be5dfe9a37bacf9baf8b4a0b07907b.png) כך ש
כך ש
- הוכיחו/הפריכו: קיימת
![[\hat{T}\circ T]_{B}^{B} =\left(\begin{array}{ccc}
1 & 0 & 0\\
0 & 2 & 0\\
0 & 0 & 0
\end{array}\right)](/images/math/3/9/5/39566d9c91db9b5cdcb780f931a99fbe.png) וגם
וגם
![[T\circ\hat{T}]_{S}^{C} =\left(\begin{array}{ccc}
1 & 0 & 0\\
0 & 2 & 0\\
0 & 0 & 3
\end{array}\right)](/images/math/0/c/2/0c2982949277e697efebbcef6a568d66.png)
- מצאו לאילו ערכי
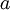 קיימת
קיימת ![\hat{T}:\mathbb{R}_{2}[x]\to\mathbb{R}_{2}[x]](/images/math/4/7/b/47be5dfe9a37bacf9baf8b4a0b07907b.png) כך ש
כך ש
- מצאו לאילו ערכי
![[\hat{T}\circ T]_{C}^{B} =\left(\begin{array}{ccc}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & a
\end{array}\right)](/images/math/8/9/f/89f3733ad1526fbc6919562848689cdf.png)
אלגוריתם למציאת מטריצה המייצגת את ההעתקה בין בסיסים כלשהם
הנה אלגוריתם שמכליל את הדוגמא הקודמת.
יהיו מ"ו V,W והעתקה T בינהם ובסיסים E,F בדיוק כמו בהגדרה לעיל. אזי:
- מצא את מטריצת המעבר
![[I]^F_S](/images/math/9/c/8/9c891851116631d866f8316d8559a34b.png) (קל, לשים את הקואורדינטות לפי הבסיס הסטנדרטי של איברי F בעמודות)
(קל, לשים את הקואורדינטות לפי הבסיס הסטנדרטי של איברי F בעמודות) - הפוך אותה על מנת לקבל את
![[I]^S_F](/images/math/f/f/4/ff48ee9930528f63e9a01fa9b5313b11.png)
- הפעל את ההעתקה T על איברי הבסיס E לקבל
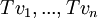
- שים את הקואורדינטות לפי הבסיס הסטנדרטי של התמונות משלב שלוש בעמודות מטריצה
![[T]^E_S](/images/math/5/e/8/5e82090d1f89376b1881037a7b72f065.png)
- כפול מטריצות על מנת לקבל
![[T]^E_F=[I]^S_F[T]^E_S](/images/math/c/a/8/ca8b2beac728b6465d3317ff79c2481c.png)
אלגוריתם למציאת העתקה מפורשת לפי תמונות איברי הבסיס בלבד
תהי T העתקה לינארית הנתונה על ידי התמונות של איברי בסיס 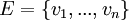 . רוצים למצוא את
. רוצים למצוא את 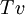 עבור
עבור 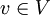 וקטור כלשהו.
וקטור כלשהו.
- נבצע את האלגוריתם לעיל על מנת למצוא את
![[T]^E_S](/images/math/5/e/8/5e82090d1f89376b1881037a7b72f065.png) .
. - נכפול במטריצת המעבר על מנת לקבל
![[T]=[T]^S_S=[T]^E_S[I]^S_E](/images/math/e/b/d/ebd654853fc72adac9cb4d06e9a6aae8.png)
![[T][v]=[Tv]](/images/math/c/6/8/c6805daa449e0209f6b1562c08ab372e.png) מכיוון שכל אלה בבסיס הסטנדרטי, נכפול בוקטור כללי מהמרחב על מנת למצוא לאן הוא נשלח במפורש.
מכיוון שכל אלה בבסיס הסטנדרטי, נכפול בוקטור כללי מהמרחב על מנת למצוא לאן הוא נשלח במפורש.
דוגמא
תרגיל. יהיו 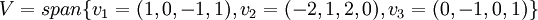 ו
ו ![W=\mathbb{R}_3[x]](/images/math/5/b/1/5b11543f95562afb073d8a5929444659.png) מ"ו. תהי העתקה T מV לW המקיימת
מ"ו. תהי העתקה T מV לW המקיימת 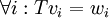 כאשר
כאשר
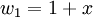
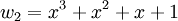
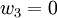
מצא את ההעתקה T במפורש.
פתרון
דבר ראשון נמצא את המטריצה המייצגת מ 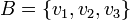 לבסיס הסטדנרטי של הפולינומים S. נשים את התמונות בעמודות
לבסיס הסטדנרטי של הפולינומים S. נשים את התמונות בעמודות
![[T]^B_S =\begin{pmatrix}
| & | & | \\
\big[Tv_1]_S & [Tv_2]_S &[Tv_3]_S \\
| & | & | \\
\end{pmatrix}=
\begin{pmatrix}
| & | & | \\
\big[w_1]_S & [w_2]_S &[w_3]_S \\
| & | & | \\
\end{pmatrix}=
\begin{pmatrix}
1 & 1 & 0 \\
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 1 & 0 \\
\end{pmatrix}](/images/math/0/d/b/0db50229316c406d6a327d5aba23b90c.png)
כעת נמצא את מטריצת המעבר. שימו לב שאנו עוסקים במקרה מיוחד. המרחב שלנו אינו מרחב מוכר, ואנו צריכים למצוא לו בסיס סטנרטי על מנת לקחת את הקואורדינטות של איברי הבסיס הנתון לפי אותו בסיס סטנדרטי שנמציא. נדרג מטריצה ששורתיה עם הוקטורים הנ"ל. כיוון שמרחב השורות לא משתנה נקבל בסיס אחר יותר נח.
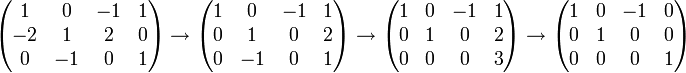 ולכן בסיס אלטרנטיבי למרחב שלנו הוא
ולכן בסיס אלטרנטיבי למרחב שלנו הוא
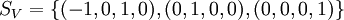 . מדוע הוא סטנדרטי? קל מאד לראות שלכל וקטור במרחב
. מדוע הוא סטנדרטי? קל מאד לראות שלכל וקטור במרחב ![[(-x,y,x,z)]_{S_V}=(x,y,z)](/images/math/c/3/5/c35dc589e5e1d221507334cd71bcd01e.png) .
.
כעת נמצא מטריצת מעבר ![[I]^B_{S_V}=
\begin{pmatrix}
-1 & 2 & 0 \\
0 & 1 & -1 \\
1 & 0 & 1 \\
\end{pmatrix}](/images/math/8/6/3/86386eefb26172c1476f51fd45e139ae.png)
נהפוכו על מנת לקבל:
![[I]^{S_V}_B=([I]^B_{S_V})^{-1}=\frac{1}{3}
\begin{pmatrix}
-1 & 2 & 2 \\
1 & 1 & 1 \\
1 & -2 & 1 \\
\end{pmatrix}](/images/math/a/3/7/a37ba815baeee670c1edfe917551ff4d.png)
ביחד אנו מקבלים
![[T]^{S_V}_S=[T]^{B}_S\cdot [I]^{S_V}_B=
\begin{pmatrix}
1 & 1 & 0 \\
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 1 & 0 \\
\end{pmatrix}
\cdot
\frac{1}{3}
\begin{pmatrix}
-1 & 2 & 2 \\
1 & 1 & 1 \\
1 & -2 & 1 \\
\end{pmatrix}
=
\frac{1}{3}
\begin{pmatrix}
0 & 3 & 3 \\
0 & 3 & 3 \\
1 & 1 & 1 \\
1 & 1 & 1 \\
\end{pmatrix}](/images/math/7/e/8/7e8a83f93d7510d4014b78c9daa4c7b6.png)
לכן, ![[T(-x,y,x,z)]_S=[T]^{S_V}_S[(-x,y,x,z)]_{S_V}=
\frac{1}{3}
\begin{pmatrix}
0 & 3 & 3 \\
0 & 3 & 3 \\
1 & 1 & 1 \\
1 & 1 & 1 \\
\end{pmatrix}
\cdot
\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix}
=
\begin{pmatrix}
y+z \\
y+z \\
\frac{1}{3}(x+y+z) \\
\frac{1}{3}(x+y+z) \\
\end{pmatrix}](/images/math/a/1/b/a1b0bcd045e4931e7df39e6ed5b7ec27.png)
ולכן בסופו של דבר:
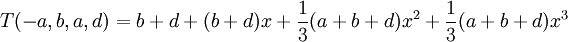
מחלקת שקילות של מטריצות המייצגות העתקה
טענה: יהא  מ"ו מימד סופי
מ"ו מימד סופי 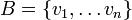 בסיס. תהא
בסיס. תהא 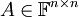 הפיכה.
אזי קיים
הפיכה.
אזי קיים 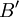 בסיס אחר כך ש
בסיס אחר כך ש ![[I]^{B'}_B= A](/images/math/c/f/5/cf5e8a854e8db8413a57ef254fc77f58.png)
(במילים: המטריצה A היא מטריצת מעבר מאיזה שהוא בסיס אחר לבסיס הנתון)
הוכחה: נגדיר 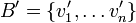 ע"י
ע"י 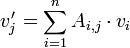 .
לפי הגדרה מתקיים כי
.
לפי הגדרה מתקיים כי ![[I]^{B'}_B= A](/images/math/c/f/5/cf5e8a854e8db8413a57ef254fc77f58.png) . נותר להוכיח כי אכן
. נותר להוכיח כי אכן 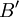 בסיס.
כיוון ש
בסיס.
כיוון ש 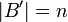 אזי אם נוכיח כי
אזי אם נוכיח כי 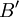 בת"ל אזי הוא בסיס לפי השלישי חינם.
בת"ל אזי הוא בסיס לפי השלישי חינם.
נוכיח כי 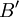 בת"ל
בת"ל
נניח כי 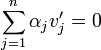 . צ"ל כי
. צ"ל כי 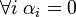
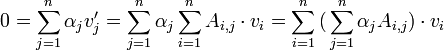
כיוון ש  בת"ל נקבל כי לכל
בת"ל נקבל כי לכל 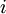 מתקיים כי
מתקיים כי 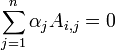
אבל זה בדיוק הקורדינאטה ה 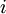 - ית של הכפל
- ית של הכפל 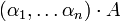
ולכן 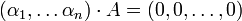 ע"י הכפלה מימין ב
ע"י הכפלה מימין ב 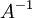 נקבל את הדרוש.
נקבל את הדרוש.
בניה:
על המטריצות הריבועיות 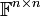 נגדיר יחס שקילות באופן הבא:
נגדיר יחס שקילות באופן הבא:
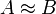 אם קיימת מטריצה הפיכה
אם קיימת מטריצה הפיכה 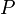 כך ש
כך ש 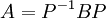 .
.
יחס זה נקרא "הצמדה".
הוכיחו כי זהו אכן יחס שקילות.
טענה מרכזית
יהא  מ"ו מימד סופי
מ"ו מימד סופי  . תהא
. תהא 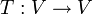 ה"ל.
ונשתמש בסימון
ה"ל.
ונשתמש בסימון 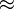 כיחס ההצמדה על המטריצות
כיחס ההצמדה על המטריצות 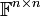 שהגדרנו לעיל.
שהגדרנו לעיל.
מתקיים כי
1. ![[T]_B \approx [T]_{B'}](/images/math/b/6/5/b65ba9a915d5c0b7077a4f46ab6f811a.png) עבור כל 2 בסיסים
עבור כל 2 בסיסים 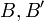
2. אם ![[T]_B \approx A](/images/math/7/3/1/73102b0f623357e4af4e0bf504edee59.png) עבור
עבור  בסיס כל שהוא אזי קיים בסיס
בסיס כל שהוא אזי קיים בסיס 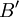 כך ש
כך ש ![[T]_{B'}=A](/images/math/5/7/0/57064392845c1be67058772deff13722.png)
במילים- המטריצה המייצגת של 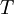 יחידה עד כדי הצמדה.
יחידה עד כדי הצמדה.
כלומר אם נייצג את 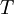 ע"י 2 בסיסים נקבל מטריצות צמודות ומאידך גיסא אם יש מטריצה
ע"י 2 בסיסים נקבל מטריצות צמודות ומאידך גיסא אם יש מטריצה  הצמודה לאיזה שהוא מטריצה מייצגת של
הצמודה לאיזה שהוא מטריצה מייצגת של 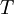 אז גם המטריצה
אז גם המטריצה  מייצגת את
מייצגת את 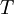
הוכחה:
1. מתקיים בגלל השיוויון ![[T]^B_B=[I]^{B'}_B[T]^{B'}_{B'}[I]^B_{B'}](/images/math/9/e/f/9ef20fbba0ecb14eb5ddd62411d36e37.png) ומתקיים כי
ומתקיים כי ![[I]^{B'}_B](/images/math/c/6/c/c6c3e3bb9bd1842dec9878a5848f742a.png) הופכית של
הופכית של ![[I]^B_{B'}](/images/math/2/c/2/2c29f373c050e153d75ce612a733d64b.png)
2. נתון כי קיימת מטריצה הפיכה 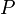 כך ש
כך ש ![P^{-1}[T]_BP = A](/images/math/1/f/4/1f4044667dd29a355f6a2a82875a44eb.png) מהטענה שהוכחנו לעיל קיים בסיס
מהטענה שהוכחנו לעיל קיים בסיס 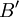 כך ש
כך ש ![[I]^{B'}_B= P](/images/math/b/b/a/bba491b2b8321f7d7019e7eddf6fa1ac.png) ואז
ואז ![A=P^{-1}[T]_BP = [I]^B_{B'}[T]_B[I]^{B'}_B=[T]^{B'}_{B'}](/images/math/e/1/6/e16315faa3e28cb5121a4860d1c5e787.png) כלומר
כלומר  אכן מייצגת את
אכן מייצגת את 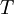 לפי הבסיס
לפי הבסיס 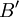 .
.
הגדרה:
יהא  מ"ו מימד סופי
מ"ו מימד סופי  . תהא
. תהא 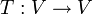 ה"ל.
ה"ל.
אזי העקבה של 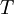 מוגדרת להיות
מוגדרת להיות
![trace(T)=trace([T]_B)](/images/math/8/3/1/831668e2c10e8c3e0641d7587ff1618e.png) כאשר
כאשר  בסיס כלשהוא. (או בקיצור
בסיס כלשהוא. (או בקיצור ![tr([T]_B)](/images/math/2/8/6/2867c4e9909e73597f7ed277c1953f2f.png) )
)
הערה: ההגדרה לא תלויה בבחירת הבסיס. כלומר עבור 2 בסיסים 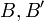 מתקיים כי
מתקיים כי ![trace([T]_{B'})=trace([T]_B)](/images/math/3/9/e/39e418a55121d85512c6665e681375b4.png) .
.
למה? לפי הטענה המרכזית קיימת 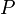 הפיכה כך ש
הפיכה כך ש
![[T]_B=P^{-1}[T]_{B'}P](/images/math/e/7/9/e793027e4063a4ff3c222022cde2b97b.png) ואז מתקיים
ואז מתקיים ![tr([T]_B)=tr(P^{-1}[T]_{B'}P)=tr(PP^{-1}[T]_{B'})=tr([T]_{B'})](/images/math/d/c/e/dcec33eec02d801f6f1236c05fc528b5.png)
המעבר באמצע נובע מהעובדה כי לכל 2 מטריצות 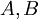 מתקיים כי
מתקיים כי