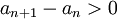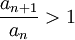הבדלים בין גרסאות בדף "88-132 סמסטר א' תשעא"
(←הודעות) |
(←הודעות) |
||
| שורה 7: | שורה 7: | ||
==הודעות== | ==הודעות== | ||
| + | |||
| + | ===דוגמאות לתרגילים על סדרות קושי=== | ||
| + | [[דוגמאות להוכחת התכנסות באמצעות קריטריון קושי| דוגמאות.]] | ||
===תיקון בנושא נקודות הצטברות לתלמידים של ארז שיינר=== | ===תיקון בנושא נקודות הצטברות לתלמידים של ארז שיינר=== | ||
גרסה מ־12:36, 8 בנובמבר 2010
תוכן עניינים
קישורים
הודעות
דוגמאות לתרגילים על סדרות קושי
תיקון בנושא נקודות הצטברות לתלמידים של ארז שיינר
בכיתה השמטתי חלק מההגדרה, הנה ההגדרה המדוייקת:
תהי 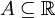 , ותהי
, ותהי 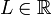 . נקודה L נקראת נקודת הצטברות של A אם לכל קבוצה פתוחה שמכילה את L (נסמן אותה ב
. נקודה L נקראת נקודת הצטברות של A אם לכל קבוצה פתוחה שמכילה את L (נסמן אותה ב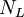 ) מתקיים
) מתקיים 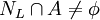 וגם
וגם 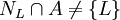 . במילים אחרות, קיימת נקודה
. במילים אחרות, קיימת נקודה 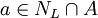 כך ש
כך ש 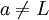 .
.
אני חושב אבל שיותר פשוט להבין את ההגדרה הבאה ללא קבוצות פתוחות (אלו הגדרות שקולות):
תהי 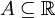 , ותהי
, ותהי 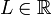 . נקודה L נקראת נקודת הצטברות של A אם לכל
. נקודה L נקראת נקודת הצטברות של A אם לכל 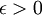 קיים
קיים 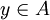 כך ש
כך ש 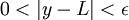 .
.
הגדרה: קבוצה סגורה הינה קבוצה המכילה את כל נקודות ההצטברות שלה.
תיקון לתרגיל 5
שימו לב לתיקון בתרגיל 5 שאלה 4 --ארז שיינר 13:58, 8 בנובמבר 2010 (IST)
בוחן לתלמידים של פרופ' זלצמן
בתאריך 22/11/01 יתקיים בוחן על חשבון ההרצאה של אינפי לשתי הקבוצות של פרופ' זלצמן.
החומר לבוחן הוא כל מה שנלמד בתרגול ובהרצאה עד לשבוע הבוחן (לא כולל יום ראשון בשבוע של הבוחן), סגנון הבוחן דומה לתרגיל (התרגיל בכיתה ותרגילי הבית)
דגשים:
- יש לדעת לצטט במדוייק את כל ההגדרות והמשפטים שנלמדו, תהיה שאלה של ציטוט הגדרות ומשפטים.
- יש לעבור על שיעורי הבית (ראה הודעה קודמת) תהיה שאלה מתוך שיעורי הבית (מן הסתם מהשאלות הפחות טריוויאליות).
- פתרון הבוחן צריך להעשות על ידי הוכחות מתמטיות בלבד. טיעוניים של 'בערך' לא יקבלו ניקוד כלל.
- ניתן להסתכל בבוחן משנה שעברה. המבנה אינו חייב להיות זהה, אבל זה תרגול טוב. פתרון יפורסם בהמשך
- מטרת הבוחן, מלבד הציון, הינה להציב מולכם מראה של מצבכם הנוכחי. גם אם לא תצליחו בבוחן, אל תתייאשו - יש זמן לתקן עד המבחן.
בהצלחה.
קריאת פתרונות התרגילים באתר
קריאת פתרונות התרגילים המפורסמים באתר הינה בגדר חובה לכל תלמידי הקורס ללא תלות בציון תרגילי הבית שהוגשו. לעיתים קרובות טעויות מהותיות מתפספסות בבדיקה ואחרי כן טעויות אלה מוצאות את דרכן אל עבר דפי המבחן. אם נדמה לך שפתרת תרגיל מסוים בדרך מהירה יותר מאשר זו הרשומה באתר, דאג להבין גם את הדרך בפתרון שלנו.
כמובן שאם מצאתם טעות בפתרון המפורסם באתר, עליכם להודיע על כך במהרה על מנת שנוכל לתקנו.
הגדרת limsup ,liminf
תהי סדרה 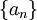 .
.
נגדיר סדרה 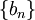 באופן הבא:
באופן הבא: 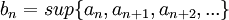 ,
,
אזי 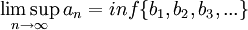
נגדיר סדרה 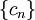 באופן הבא:
באופן הבא:  ,
,
אזי 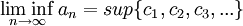
במילים, אנחנו מחפשים את החסמים העליונים והתחתונים של הסדרה, שנשמרים לאורך הסדרה ולא נקבעים על ידי מספר סופי של איברים, לכן אנו מסתכלים על החסם של קבוצת חסמי הסדרה אחרי השמטת n איברים הראשונים.
סדרות מונוטוניות
על מנת להוכיח שסדרה היא מונוטונית עולה, מספיק להוכיח את אחד התנאים הבאים (לכל n):
שני התנאים גוררים את אי השיוויון 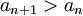
גבול של סדרה
תהי סדרת מספרים ממשיים 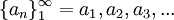 , (כך ש
, (כך ש 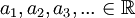 ).
).
לדוגמא:
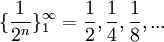
גבול של סדרה הוא נקודה ממשית אליה איברי הסדרה מתקרבים. לסדרה שלא מתקרבת לנקודה ספציפית אין גבול, למשל: 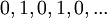 (לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדוייק:
(לסדרה זו אין גבול). נגדיר את מושג הגבול באופן מדוייק:
הגדרת הגבול
תהי 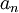 סדרה של מספרים ממשיים. אזי מספר ממשי
סדרה של מספרים ממשיים. אזי מספר ממשי 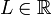 נקרא גבול הסדרה
נקרא גבול הסדרה 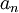 אם לכל
אם לכל 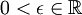 קיים
קיים 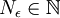 כך שלכל
כך שלכל 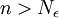 מתקיים
מתקיים 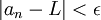 .
.
הסבר ההגדרה
נתרגם את זה למילים. למדנו ש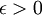 מודד אורך, מספר טבעי
מודד אורך, מספר טבעי 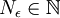 מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האיברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
מסמל מקום בסדרה, וערך מוחלט של הפרש מודד מרחק בין שני האיברים. בנוסף למדנו על המשפט הלוגי 'לכל סיר יש מכסה שמתאים לו'. עכשיו נרשום את הגדרת הגבול במילים:
נקודה L על ציר המספרים הממשיים היא גבול הסדרה 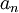
אם לכל אורך (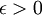 ) [סיר]
) [סיר]
קיים מקום בסדרה (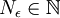 ) [מכסה]
) [מכסה]
כך שהחל ממנו והלאה (לכל 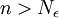 ) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך
) מתקיים שהמרחק בין איברי הסדרה לבין הנקודה L קטן מהאורך 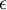 (
(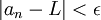 ) [מתאים לו]
) [מתאים לו]
הגדרות
חובה לדעת את ההגדרות באופן מדוייק במהלך כל השנה. הגדרות כמו חסם מלעיל, חסם עליון, שדה שלם וכדומה. אתם גם עשויים להבחן על הגדרות אלו.
ידיעה של ההגדרות מקלה פי כמה על הבנת ההוכחות והמושגים החדשים שנלמדים בקורס, שכן מושגים, משפטים והוכחות נשענים על החומר שקדם להם.
הגשת תרגילים
הגשת תרגילים תתבצע כך:
- דפים משודכים עם שדכן בצד ימין למעלה. (ללא ניילוניות!).
- על העמוד הראשי יש לציין: שם המגיש, תעודת זהות, שם המתרגל.
- את התרגיל יש להגיש כל שבוע למתרגל בעת השיעור (החל משבוע הבא - בו תגישו את התרגיל הראשון).
- אין להשאיר תרגילים בתא המתרגל (אלא לפי אישור מפורש במקרים חריגים).
ידע נדרש
ברוכים הבאים לקורס אינפי !!!!1
על מנת להצליח בקורס, אתם נדרשים (בין היתר) לדעת היטב את הנושאים הבאים:
- טריגונומטריה (קוסינוסים, סינוסים וכדומה, מתי הפונקציות הטריגונומטריות מתאפסות, מתי מגיעות למקס/מינ, נוסחאות טריגונומטריות, רדיאנים...)
- לוגים
- אינדוקציה