הבדלים בין גרסאות בדף "88-133 אינפי 2 תשעב סמסטר ב/פתרון מועד א"

גרסה מ־15:08, 19 ביולי 2012

תוכן עניינים

1 1
2 2
- 2.1 א
- 2.2 ב
- 2.3 ג
3 3
- 3.1 א
- 3.2 ב
4 4

1

שאלת הוכחה מההרצאה

2

חשבו את האינטגרלים הבאים:

א

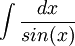
$\int\frac{dx}{sin(x)}$

פתרון:

נבצע הצבה אוניברסאלית 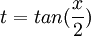$t=tan(\frac{x}{2})$ לקבל

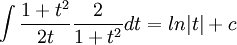
$\int\frac{1+t^2}{2t}\frac{2}{1+t^2}dt=ln|t|+c$

ב

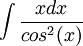
$\int\frac{xdx}{cos^2(x)}$

נבצע אינטגרציה בחלקים לקבל

$\int\frac{xdx}{cos^2(x)}=xtan(x)-\int tan(x) = xtan(x)-ln|cos(x)|+c$

ג

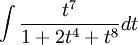
$\int\frac{t^7}{1+2t^4+t^8}dt$

ניתן לבצע את האלגוריתם לביצוע אינטגרל על פונקציה רציונאלית

או ההצבה 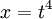$x=t^4$ באופן הבא:

$\int \frac{t^7}{1+2t^4+t^8}dt=\int\frac{x}{4(1+2x+x^2)}dx=\frac{1}{8}\int\frac{2x+2-2}{(1+x)^2}dx=\frac{1}{8}ln[(1+x)^2]+\frac{1}{4}\frac{1}{1+x}+c$

3

א

קבעו האם האינטגרל הבא מתכנס או מתבדר:

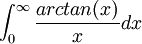
$\int_0^\infty\frac{arctan(x)}{x}dx$

פתרון: כיוון ש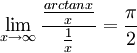 $\lim_{x\rightarrow\infty}\frac{\frac{arctanx}{x}}{\frac{1}{x}}=\frac{\pi}{2}$

וכיוון ש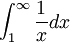 $\int_1^\infty\frac{1}{x}dx$ מתבדר

שני האינטגרלים חברים ומתבדרים יחדיו.

ב

הוכיחו שאם 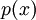$p(x)$ פולינום שאינו שווה זהותית לאפס, אזי האינטגרל 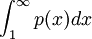$\int_1^\infty p(x)dx$ מתבדר.

פתרון:

אם הפולינום אינו זהותית אפס, האינטגרל הלא מסויים שלו 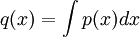$q(x)=\int p(x)dx$ בעל מעלה גדולה או שווה לאחד. ולכן

$\int_1^\infty p(x)dx=\lim_{b\rightarrow\infty}\int_1^b p(x)dx=\lim_{b\rightarrow\infty}[q(b)-q(1)]=\infty$

האחרון מתבדר כיוון שהמעלה של q גדולה או שווה לאחד.

4

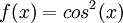מצאו את טור מקלורין של הפונקציה $f(x)=cos^2(x)$ וקבעו את רדיוס ההתכנסות של הטור.

פתרון:

@@ שורה 60: / שורה 60: @@
 האחרון מתבדר כיוון שהמעלה של q גדולה או שווה לאחד.
+==4==
+מצאו את טור מקלורין של הפונקציה <math>f(x)=cos^2(x)</math> וקבעו את רדיוס ההתכנסות של הטור.
+'''פתרון''':

הבדלים בין גרסאות בדף "88-133 אינפי 2 תשעב סמסטר ב/פתרון מועד א"

גרסה מ־15:08, 19 ביולי 2012

תוכן עניינים

1

2

א

ב

ג

3

א

ב

4

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים