הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 0"
מתוך Math-Wiki
(←טבלאות אמת) |
(←טבלאות אמת) |
||
| שורה 16: | שורה 16: | ||
==טבלאות אמת== | ==טבלאות אמת== | ||
| − | הוכח באמצעות טבלאות אמת שניתן להציג את הקשרים 'גרירה' ו'וגם' באמצעות 'או' ושלילה בלבד | + | *הוכח באמצעות טבלאות אמת שניתן להציג את הקשרים 'גרירה' ו'וגם' באמצעות 'או' ושלילה בלבד |
| + | הוכח אחד או יותר מבין טאוטולוגיות הבאות (נציג בהזדמנות זאת את המושג טאוטולוגיה) | ||
| + | * <math>\ \neg\neg A \equiv A</math> | ||
| + | * <math>\ (A\rightarrow B) \equiv ((\neg A) \vee B)</math>. | ||
| + | * <math>\ (A \leftrightarrow B) \equiv ((A \wedge B)\vee((\neg A)\wedge (\neg B)</math>. | ||
| + | * <math>\ (A \leftrightarrow B) \equiv (A \rightarrow B) \wedge (B \rightarrow A)</math>. | ||
| + | * <math>\ (A \rightarrow B) \equiv ((\neg B) \rightarrow (\neg A))</math>. | ||
גרסה מ־09:56, 8 ביולי 2012
סיכום הנושא המלא נמצא בדף 88-101 חשיבה מתמטית.
קשרים, כמתים, הצרנה
ראשית, נכיר את הקשרים הלוגיים (וגם, או, שלילה, גורר), הכמתים (לכל, קיים) ואת מושג ההצרנה.
תרגיל: הגדרה: איחוד של שתי קבוצות A וB הוא קבוצת האיברים שנמצאים לפחות באחת הקבוצות. החיתוך הוא קבוצת האיברים שנמצאים בשתי הקבוצות.
- הצרן תנאי השקול לכך ש-a שייך לאיחוד של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a אינו שייך לאיחוד של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a שייך לחיתוך של הקבוצות A וB
- הצרן תנאי השקול לכך ש-a אינו שייך לחיתוך של הקבוצות A וB
הגדרה: קבוצה A מוכלת בקבוצה B אם בB נמצאים כל האיברים מA (למשל הטבעיים מוכלים בשלמים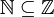 
, והשלמים מוכלים בממשיים 
).
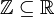- הצרן תנאי השקול לכך ש-C מוכלת בחיתוך של A וB
- הצרן תנאי השקול לכך ש-C אינה מוכלת באיחוד של A וB
טבלאות אמת
- הוכח באמצעות טבלאות אמת שניתן להציג את הקשרים 'גרירה' ו'וגם' באמצעות 'או' ושלילה בלבד
הוכח אחד או יותר מבין טאוטולוגיות הבאות (נציג בהזדמנות זאת את המושג טאוטולוגיה)
-
-
. -
. -
. -
.
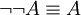
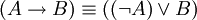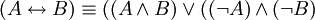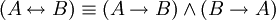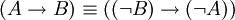