הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 11"
אחיה בר-און (שיחה | תרומות) (←תרגיל) |
(עריכה) |
||
| שורה 2: | שורה 2: | ||
= הגדרות בסיסיות = | = הגדרות בסיסיות = | ||
| − | '''הגדרה''' | + | '''הגדרה''': '''גרף''' <math>G</math> מעל קבוצה <math>V</math> הוא זוג סדור <math>G=(V,E)</math> כאשר math>E \subseteq V\times V</math> - כלומר קבוצה המכילה זוגות סדורים מאיברי <math>V</math>. |
| − | + | ||
| − | + | הקבוצה <math>V</math> היא קבוצת ה'''קדקודים''' של הגרף, והקבוצה <math>E</math> היא קבוצת הקשתות/צלעות של הגרף. | |
| − | + | ||
| + | '''הגדרה''': הסדר של גרף <math>G=(V,E)</math> הוא <math>|V|</math>. גרף יקרא סופי אם הסדר שלו סופי, וקבוצת הקשתות <math>E</math> סופית. | ||
| − | + | '''הגדרה''': גרף <math>G</math> ייקרא '''לא מכוון''' אם היחס <math>E</math> הוא סימטרי, כלומר אין משמעות לכיוון הצלע. אחרת הגרף ייקרא מכוון. בגרף לא מכוון, אין משמעות לכיוון הצלע, ולכן לעתים מסמנים <math>(u,v)</math> בתור <math>\{u,v\}</math>. | |
| + | '''דוגמא''': <math>V=\{1,2,3\}, E=\Big\{\{1,2\},\{2,3\},\{1,3\}\Big\}</math> מייצג משולש. הסדר שלו הוא 3, כמספר הצלעות במשולש, ובפרט הוא סופי. | ||
| − | ''' | + | '''הערה''': שימו לב שמהניסוח לעיל נובע- |
| + | # בגרף יכולה להיות קשת מקדקוד אל עצמו (לולאה). זה שקול ל- <math>\exists (v,v) \in E</math>. | ||
| + | #צלע בין שני קדקודים יכולה להופיע אך ורק פעם אחת (כי <math>E</math> קבוצה). בפועל, יש גרפים שבהם מופיעה יותר מצלע אחת בין שני קדקודים (למשל שתי לולאות סביב נקודה). נסו לחשוב איך להגדיר את זה פורמלית. | ||
| + | '''הבהרה: אנחנו נעסוק בגרפים סופיים, לא מכוונים, בלי צלעות כפולות ובלי לולאות'''. | ||
| − | + | '''הגדרה''' יהיה <math>G=(V,E)</math>. נאמר כי <math>v,w\in V</math> '''שכנים''' אם <math>(v,w)\in E</math>. במקרה זה נאמר כי הצלע <math>\{v,w\}\in E</math> חלה ב <math>w</math> (או חלה ב <math>v</math>) | |
| + | את קבוצת השכנים של <math>u</math> מסמנים <math>\Gamma(u)=\{v\in V \; :\; \{v,u\}\in E\}</math>. | ||
| − | ''' | + | ה'''דרגה''' של <math>u</math>, המסומנת <math>\text{degree}(u)</math>, היא מספר הצלעות החלות ב <math>u</math>, כלומר <math>|\Gamma(u)|</math>. |
| − | |||
| − | + | '''דוגמא:''' במשולש, כל 2 קדקודים שכנים. כל קדקוד מדרגה 2: השכנים של כל קדקוד הם שני הקדקודים האחרים. | |
| − | |||
| + | ==משפט (לחיצת הידיים)== | ||
| + | יהי <math>G=(V,E)</math> גרף לא מכוון. אזי <math>\sum_{v\in V}\text{degree}(v)=2|E|</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== תרגיל === | === תרגיל === | ||
| − | + | נאמר כי גרף <math>G=(V,E)</math> הוא '''<math>k</math>-רגולרי''' אם כל הדרגה של כל קדקוד שווה ל-<math>k</math>. | |
| − | הוכח כי לא קיים גרף k-רגולרי מסדר n | + | הוכח כי אם <math>k,n</math> אי-זוגיים, לא קיים גרף <math>k</math>-רגולרי מסדר <math>n</math>. |
הוכחה: | הוכחה: | ||
| − | + | לפי משפט לחיצת הידיים <math>2|E|=\sum_{v\in V}\text{degree}(v)=n\cdot k</math>. אבל מכפלה של מספרים אי זוגיים היא אי-זוגית, ולכן <math>k</math> זוגי או <math>n</math> זוגי. | |
| − | |||
| + | ==הגדרות נוספות== | ||
| − | = | + | יהי <math>G=(V,E)</math> גרף לא מכוון. סדרת קדקודים (סדורה) <math>(v_0,v_1,\dots,v_n)</math> נקראת '''מסלול''' אם <math>\forall i : \{v_i,v_{i+1}\}\in E</math> וגם כל הצלעות שונות - כלומר לכל <math>i\neq j</math> מתקיים <math>(v_i,v_{i+1}) \neq (v_j,v_{j+1})</math>. |
| − | + | מסלול יקרא '''פשוט''' אם כל הקדקודים <math>(v_0,v_1,\dots,v_n)</math> שונים זה מזה, פרט אולי ל <math>v_0=v_n</math>, ובמקרה זה המסלול נקרא '''מעגל'''. אורך המסלול <math>(v_0,v_1,\dots,v_n)</math> הוא <math>n</math>, והנקודות <math>v_0</math> ו-<math>v_n</math> נקראות '''נקודות ההתחלה והסיום''' של המסלול. | |
| − | <math> | + | |
| − | + | '''הגדרה''': המרחק בין <math>v,u\in V</math> הוא המסלול עם אורך מינימלי בין <math>v,u\in V</math>. אם אין מסלול בין הנקודות, אומרים שהמרחק הוא אינסוף. מסמנים את המרחק <math>d(u,v)</math>, ואם יש צורך להדגיש את הגרפים אז מסמנים <math>d_G(u,v)</math>. | |
| − | + | ה'''קוטר''' של גרף <math>G=(V,E)</math> מוגדר כמרחק המקסימאלי בין זוגות קדקודים - כלומר <math>\text{diam}(G)=\max_{u,v\in V}{d(v,u)}</math> | |
| − | + | ===בניה=== | |
| + | עבור גרף לא מכוון <math>G=(V,E)</math> נגדיר יחס שקילות <math>\to </math> על <math>V</math>, כך: לכל <math> v,u\in V</math> מתקיים <math> v\to u</math> אמ"מ קיים מסלול מ<math>v</math> ל-<math>u</math> (כלומר <math>u \to v \iff d(v,u)<\infty </math>). | ||
| − | + | '''תרגיל''': הוכח כי זהו יחס שקילות. | |
| − | ''' | + | '''פתרון''': |
| + | # ''רפלקסיבי'' - לכל קדקוד, המסלול <math>(v)</math> עושה את העבודה. | ||
| + | # ''סימטרי'' - אם <math> v\to u</math>, אז יש מסלול <math> (v_0,\dots,v_n)</math> בין <math>v</math> ל-<math>u</math>. נביט במסלול ההפוך - <math> (v_n, v_{n-1}\dots ,v_1,v_0)</math> - זהו מסלול בין <math>u</math> ל-<math>v</math>, ולכן <math>u \to v</math>. | ||
| + | # ''טרנזיטיבי'' - אם <math> v\to u</math> וגם <math> u\to t</math>, אז יש מסלולים <math> (v_1,\dots,v_n)</math> ו-<math> (v_1',\dots,v_n')</math>. היות ש-<math> v_n=v=v_1'</math>, נביט במסלול <math> (v_1,\dots,v_n=v_1',\dots,v_n')</math> - זהו מסלול המעיד על כך ש-<math> v\to t</math>. | ||
| − | + | '''הגדרה''' מחלקות השקילות של יחס זה נקראים רכיבי קשירות. | |
| − | + | '''דוגמא''': ציור חביב לפי דעת המתרגל. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ''' | + | |
| − | =תרגילים= | + | =תרגילים נוספים= |
| − | + | '''תרגיל''': יהי גרף לא מכוון <math>G=(V,E)</math> בעל <math>3\leq n</math> קדקודים. | |
| − | יהי גרף לא מכוון <math>G=(V,E)</math> בעל <math>3\leq n</math> | + | |
אם בגרף <math>n\leq m </math> צלעות אזי בגרף יש מעגל. | אם בגרף <math>n\leq m </math> צלעות אזי בגרף יש מעגל. | ||
| − | + | '''פתרון''': באינדוקציה. | |
| − | עבור <math>n=3</math> אזי יש מדובר במשולש (לא יכול להיות יותר מ -4 צלעות ב-3 | + | עבור <math>n=3</math> אזי יש מדובר במשולש (לא יכול להיות יותר מ -4 צלעות ב-3 קדקודים) ואכן מתקיים כי יש מעגל. |
נניח כי הטכנה נכונה עבור <math>n</math> ונוכיח עבור <math>n+1</math>. | נניח כי הטכנה נכונה עבור <math>n</math> ונוכיח עבור <math>n+1</math>. | ||
| − | יהי יהי גרף לא מכוון <math>G=(V,E)</math> בעל <math>3< n+1</math> | + | יהי יהי גרף לא מכוון <math>G=(V,E)</math> בעל <math>3< n+1</math> קדקודים ו- <math>n+1\leq m </math> צלעות. |
| − | אפשרות 1: קיים <math>v\in V</math> מדרגה 1. נוריד את | + | אפשרות 1: קיים <math>v\in V</math> מדרגה 1. נוריד את הקדקוד הזה (ואת כל הצלעות שחלות בו) ונקבל גרף חדש עם <math>n</math> קדקודים ו<math>n\leq m-1 </math> צלעות. לפי הנחת האינדוקציה קיים בו מעגל. מעגל זה קיים גם בגרף בו התחלנו. |
| − | אפשרות 2: לכל | + | אפשרות 2: לכל קדקוד יש דרגה גדולה שווה 2. נבחר <math>v_0\in V</math> ונצא ממנו לאחד משכניו. מפה נמשיך למסלול רנדומאלי כך שאם הולכים מ <math>v\to u</math> הצעד הבא לא יהיה <math>u\to v</math> (זה אפשרי כי כל קדקוד יש לפחות 2 שכנים אז אם נכנסים אליו משכן א ניתן לצאת משכן ב). כיוון שיש מספר סופי של קדקודים נקבל חזרה על קדקוד בשלב כלשהו. בפעם הראשונה שנקבל חזרה קיבלנו מעגל! |
| − | |||
| − | |||
| − | + | '''תרגיל''': יהי <math>G</math> גרף פשוט (ללא לולאות וללא צלעות מקבילות) מסדר <math>1<n</math>. הוכח שקיימים 2 קדקודים בעל אותה דרגה. | |
| − | נבנה פונקציה <math>f:V\to \{0,1,\dots n-1\} </math> המוגדרת <math>v\mapsto deg(v)</math>. | + | '''פתרון:''' נבנה פונקציה <math>f:V\to \{0,1,\dots n-1\} </math> המוגדרת <math>v\mapsto deg(v)</math>. |
| − | אם קיים | + | אם קיים קדקוד מדרגה n-1 אזי הוא מחובר לכולם ולכן אין קדקוד מדרגה אפס. במקרה זה נוכל להגדיר |
<math>f:V\to \{1,\dots n-1\} </math>. | <math>f:V\to \{1,\dots n-1\} </math>. | ||
| − | אם אין | + | אם אין קדקוד כזה אז נוכל להגדיר <math>f:V\to \{0,1,\dots n-2\} </math>. |
בשני המקרים קיבלנו כי <math>|dom(f)|=|V|=n, |Im(f)|=n-1</math> ולכן <math>f</math> אינה חח"ע. | בשני המקרים קיבלנו כי <math>|dom(f)|=|V|=n, |Im(f)|=n-1</math> ולכן <math>f</math> אינה חח"ע. | ||
כלומר קיימים <math>v_1\neq v_2</math> כך ש <math>f(v_1)=f(v_2)</math> כלומר בעלי דרגה שווה | כלומר קיימים <math>v_1\neq v_2</math> כך ש <math>f(v_1)=f(v_2)</math> כלומר בעלי דרגה שווה | ||
| − | |||
| − | |||
| − | + | '''תרגיל''': יהיה <math>G=(V,E)</math> גרף פשוט עם 100 קדקודים כך שדרגת כל קדקוד לפחות 50. הוכח כי <math>G</math> קשיר. | |
| − | + | ||
| − | == | + | '''פתרון''': יהיו <math>v,u\in V</math> צריך להוכיח כי <math>[v]=[u]</math> (כך נסמן את רכיב הקשירות). |
| + | נניח כי הם שונים אזי ב<math>|[v]|,|[u]|\geq 50</math> והם זרים. לכן <math>[v]=[u]=50</math> אבל ברכיב קשירות שיש בו 50 קדקודים דרגת כל קדקוד קטנה שווה ל 49. סתירה | ||
| − | |||
| − | + | '''תרגיל''': יהי גרף לא מכוון <math>G=(V,E)</math>. הוכח כי אם <math>\forall v\in V : \text{degree}(v)\geq 2</math> אז בגרף יש מעגל. | |
| − | + | ||
| − | + | ||
| + | '''פתרון''': בגרף יש יותר מ 2 קדקודים (אחרת לא יהיה להם 2 שכנים). | ||
| + | לפי משפט לחיצת הידיים מתקיים <math>2|E|= \sum_{v\in V}\text{degree}(v)\geq \sum_{v\in V}2 =2|V|</math> | ||
| + | ולכן מספר הצלעות גדול שווה ממספר הקדקודים. לפי משפט קודם קיים מעגל בגרף. | ||
| − | |||
| − | יהי גרף לא מכוון <math>G=(V,E)</math> ללא מעגלים עם <math>|V|\geq 2</math>. הוכח כי קיימים <math>v_1,v_2\in V</math> כך שדרגתם לכל היותר 1. | + | '''תרגיל''': יהי גרף לא מכוון <math>G=(V,E)</math> ללא מעגלים עם <math>|V|\geq 2</math>. הוכח כי קיימים <math>v_1,v_2\in V</math> כך שדרגתם לכל היותר 1. |
| − | + | '''פתרון''': לפי תרגיל קודם קיים <math>v\in V</math> כך שדרגתו לכל היותר 1 (אחרת לכל הקדקודים יש דרגה לפחות 2 ואז יש מעגל לפי תרגיל קודם. סתירה!). | |
| − | נמשיך באינדוקציה על <math>n</math> מספר | + | נמשיך באינדוקציה על <math>n</math> מספר הקדקודים בגרף. |
אם <math>n=2</math> אזי או שהגרף הוא 2 נקודות לא צלעות או 2 נקודות המחוברות בצלע. בכל מקרה 2 הנקודות של הגרף הם מדרגה קטנה שווה ל-1. | אם <math>n=2</math> אזי או שהגרף הוא 2 נקודות לא צלעות או 2 נקודות המחוברות בצלע. בכל מקרה 2 הנקודות של הגרף הם מדרגה קטנה שווה ל-1. | ||
| שורה 133: | שורה 117: | ||
כעת נניח כי הטענה נכונה עבור <math>n\geq 2</math>. נוכיח את הטענה עבור <math>n+1</math>. | כעת נניח כי הטענה נכונה עבור <math>n\geq 2</math>. נוכיח את הטענה עבור <math>n+1</math>. | ||
| − | נבחר את | + | נבחר את הקדקוד <math>v\in V</math> שדרגתו לכל היותר 1. נוריד אותו ואת הצלע שחלה בו אזי נקבל גרף עם <math>n</math> קדקודים. לפי הנחת האינדוקציה יש בו 2 קדקודים<math>v_1,v_2</math> בעלי דרגה 1 לכל היותר. כעת נשוב לגרף המקורי (הכולל את <math>v</math> שהשמטנו). |
אם <math>v</math> שכן של <math>v_1</math> אזי <math>v,v_2</math> בעלי דרגה לכל היותר 1. | אם <math>v</math> שכן של <math>v_1</math> אזי <math>v,v_2</math> בעלי דרגה לכל היותר 1. | ||
| שורה 143: | שורה 127: | ||
אם <math>v</math> לא שכן של <math>v_1,v_2</math> אזי <math>v,v_1,v_2</math> בעלי דרגה לכל היותר 1. | אם <math>v</math> לא שכן של <math>v_1,v_2</math> אזי <math>v,v_1,v_2</math> בעלי דרגה לכל היותר 1. | ||
| − | בכל מקרה קיבלנו כי קיימים 2 | + | בכל מקרה קיבלנו כי קיימים 2 קדקודים בעלי דרגה 1 לכל היותר!. |
גרסה מ־19:05, 11 באוגוסט 2015
תוכן עניינים
הגדרות בסיסיות
הגדרה: גרף 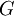 מעל קבוצה
מעל קבוצה  הוא זוג סדור
הוא זוג סדור 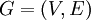 כאשר math>E \subseteq V\times V</math> - כלומר קבוצה המכילה זוגות סדורים מאיברי
כאשר math>E \subseteq V\times V</math> - כלומר קבוצה המכילה זוגות סדורים מאיברי  .
.
הקבוצה  היא קבוצת הקדקודים של הגרף, והקבוצה
היא קבוצת הקדקודים של הגרף, והקבוצה 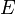 היא קבוצת הקשתות/צלעות של הגרף.
היא קבוצת הקשתות/צלעות של הגרף.
הגדרה: הסדר של גרף 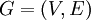 הוא
הוא 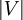 . גרף יקרא סופי אם הסדר שלו סופי, וקבוצת הקשתות
. גרף יקרא סופי אם הסדר שלו סופי, וקבוצת הקשתות 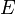 סופית.
סופית.
הגדרה: גרף 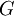 ייקרא לא מכוון אם היחס
ייקרא לא מכוון אם היחס 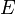 הוא סימטרי, כלומר אין משמעות לכיוון הצלע. אחרת הגרף ייקרא מכוון. בגרף לא מכוון, אין משמעות לכיוון הצלע, ולכן לעתים מסמנים
הוא סימטרי, כלומר אין משמעות לכיוון הצלע. אחרת הגרף ייקרא מכוון. בגרף לא מכוון, אין משמעות לכיוון הצלע, ולכן לעתים מסמנים 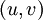 בתור
בתור 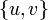 .
.
דוגמא: 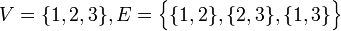 מייצג משולש. הסדר שלו הוא 3, כמספר הצלעות במשולש, ובפרט הוא סופי.
מייצג משולש. הסדר שלו הוא 3, כמספר הצלעות במשולש, ובפרט הוא סופי.
הערה: שימו לב שמהניסוח לעיל נובע-
- בגרף יכולה להיות קשת מקדקוד אל עצמו (לולאה). זה שקול ל-
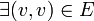 .
. - צלע בין שני קדקודים יכולה להופיע אך ורק פעם אחת (כי
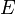 קבוצה). בפועל, יש גרפים שבהם מופיעה יותר מצלע אחת בין שני קדקודים (למשל שתי לולאות סביב נקודה). נסו לחשוב איך להגדיר את זה פורמלית.
קבוצה). בפועל, יש גרפים שבהם מופיעה יותר מצלע אחת בין שני קדקודים (למשל שתי לולאות סביב נקודה). נסו לחשוב איך להגדיר את זה פורמלית.
הבהרה: אנחנו נעסוק בגרפים סופיים, לא מכוונים, בלי צלעות כפולות ובלי לולאות.
הגדרה יהיה 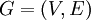 . נאמר כי
. נאמר כי 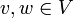 שכנים אם
שכנים אם 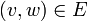 . במקרה זה נאמר כי הצלע
. במקרה זה נאמר כי הצלע 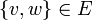 חלה ב
חלה ב 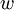 (או חלה ב
(או חלה ב 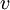 )
)
את קבוצת השכנים של 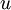 מסמנים
מסמנים 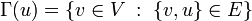 .
.
הדרגה של 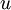 , המסומנת
, המסומנת 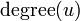 , היא מספר הצלעות החלות ב
, היא מספר הצלעות החלות ב 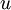 , כלומר
, כלומר 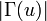 .
.
דוגמא: במשולש, כל 2 קדקודים שכנים. כל קדקוד מדרגה 2: השכנים של כל קדקוד הם שני הקדקודים האחרים.
משפט (לחיצת הידיים)
יהי 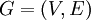 גרף לא מכוון. אזי
גרף לא מכוון. אזי 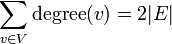 .
.
תרגיל
נאמר כי גרף 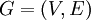 הוא
הוא 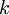 -רגולרי אם כל הדרגה של כל קדקוד שווה ל-
-רגולרי אם כל הדרגה של כל קדקוד שווה ל-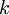 .
.
הוכח כי אם 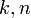 אי-זוגיים, לא קיים גרף
אי-זוגיים, לא קיים גרף 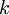 -רגולרי מסדר
-רגולרי מסדר  .
.
הוכחה:
לפי משפט לחיצת הידיים 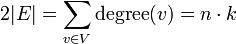 . אבל מכפלה של מספרים אי זוגיים היא אי-זוגית, ולכן
. אבל מכפלה של מספרים אי זוגיים היא אי-זוגית, ולכן 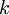 זוגי או
זוגי או  זוגי.
זוגי.
הגדרות נוספות
יהי 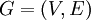 גרף לא מכוון. סדרת קדקודים (סדורה)
גרף לא מכוון. סדרת קדקודים (סדורה) 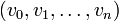 נקראת מסלול אם
נקראת מסלול אם 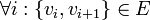 וגם כל הצלעות שונות - כלומר לכל
וגם כל הצלעות שונות - כלומר לכל 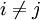 מתקיים
מתקיים 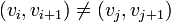 .
.
מסלול יקרא פשוט אם כל הקדקודים 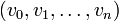 שונים זה מזה, פרט אולי ל
שונים זה מזה, פרט אולי ל 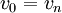 , ובמקרה זה המסלול נקרא מעגל. אורך המסלול
, ובמקרה זה המסלול נקרא מעגל. אורך המסלול 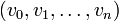 הוא
הוא  , והנקודות
, והנקודות 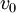 ו-
ו-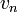 נקראות נקודות ההתחלה והסיום של המסלול.
נקראות נקודות ההתחלה והסיום של המסלול.
הגדרה: המרחק בין 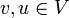 הוא המסלול עם אורך מינימלי בין
הוא המסלול עם אורך מינימלי בין 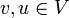 . אם אין מסלול בין הנקודות, אומרים שהמרחק הוא אינסוף. מסמנים את המרחק
. אם אין מסלול בין הנקודות, אומרים שהמרחק הוא אינסוף. מסמנים את המרחק 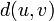 , ואם יש צורך להדגיש את הגרפים אז מסמנים
, ואם יש צורך להדגיש את הגרפים אז מסמנים 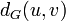 .
.
הקוטר של גרף 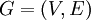 מוגדר כמרחק המקסימאלי בין זוגות קדקודים - כלומר
מוגדר כמרחק המקסימאלי בין זוגות קדקודים - כלומר 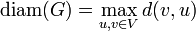
בניה
עבור גרף לא מכוון 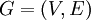 נגדיר יחס שקילות
נגדיר יחס שקילות 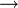 על
על  , כך: לכל
, כך: לכל 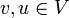 מתקיים
מתקיים 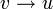 אמ"מ קיים מסלול מ
אמ"מ קיים מסלול מ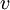 ל-
ל-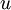 (כלומר
(כלומר  ).
).
תרגיל: הוכח כי זהו יחס שקילות.
פתרון:
- רפלקסיבי - לכל קדקוד, המסלול
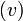 עושה את העבודה.
עושה את העבודה. - סימטרי - אם
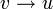 , אז יש מסלול
, אז יש מסלול 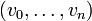 בין
בין 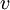 ל-
ל-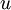 . נביט במסלול ההפוך -
. נביט במסלול ההפוך - 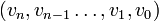 - זהו מסלול בין
- זהו מסלול בין 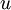 ל-
ל-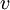 , ולכן
, ולכן 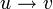 .
. - טרנזיטיבי - אם
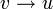 וגם
וגם 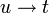 , אז יש מסלולים
, אז יש מסלולים 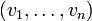 ו-
ו-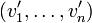 . היות ש-
. היות ש-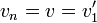 , נביט במסלול
, נביט במסלול 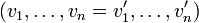 - זהו מסלול המעיד על כך ש-
- זהו מסלול המעיד על כך ש-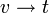 .
.
הגדרה מחלקות השקילות של יחס זה נקראים רכיבי קשירות.
דוגמא: ציור חביב לפי דעת המתרגל.
תרגילים נוספים
תרגיל: יהי גרף לא מכוון 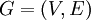 בעל
בעל 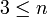 קדקודים.
אם בגרף
קדקודים.
אם בגרף 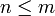 צלעות אזי בגרף יש מעגל.
צלעות אזי בגרף יש מעגל.
פתרון: באינדוקציה.
עבור 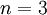 אזי יש מדובר במשולש (לא יכול להיות יותר מ -4 צלעות ב-3 קדקודים) ואכן מתקיים כי יש מעגל.
אזי יש מדובר במשולש (לא יכול להיות יותר מ -4 צלעות ב-3 קדקודים) ואכן מתקיים כי יש מעגל.
נניח כי הטכנה נכונה עבור  ונוכיח עבור
ונוכיח עבור 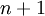 .
יהי יהי גרף לא מכוון
.
יהי יהי גרף לא מכוון 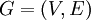 בעל
בעל 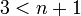 קדקודים ו-
קדקודים ו- 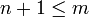 צלעות.
צלעות.
אפשרות 1: קיים 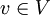 מדרגה 1. נוריד את הקדקוד הזה (ואת כל הצלעות שחלות בו) ונקבל גרף חדש עם
מדרגה 1. נוריד את הקדקוד הזה (ואת כל הצלעות שחלות בו) ונקבל גרף חדש עם  קדקודים ו
קדקודים ו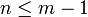 צלעות. לפי הנחת האינדוקציה קיים בו מעגל. מעגל זה קיים גם בגרף בו התחלנו.
צלעות. לפי הנחת האינדוקציה קיים בו מעגל. מעגל זה קיים גם בגרף בו התחלנו.
אפשרות 2: לכל קדקוד יש דרגה גדולה שווה 2. נבחר 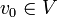 ונצא ממנו לאחד משכניו. מפה נמשיך למסלול רנדומאלי כך שאם הולכים מ
ונצא ממנו לאחד משכניו. מפה נמשיך למסלול רנדומאלי כך שאם הולכים מ 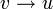 הצעד הבא לא יהיה
הצעד הבא לא יהיה 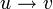 (זה אפשרי כי כל קדקוד יש לפחות 2 שכנים אז אם נכנסים אליו משכן א ניתן לצאת משכן ב). כיוון שיש מספר סופי של קדקודים נקבל חזרה על קדקוד בשלב כלשהו. בפעם הראשונה שנקבל חזרה קיבלנו מעגל!
(זה אפשרי כי כל קדקוד יש לפחות 2 שכנים אז אם נכנסים אליו משכן א ניתן לצאת משכן ב). כיוון שיש מספר סופי של קדקודים נקבל חזרה על קדקוד בשלב כלשהו. בפעם הראשונה שנקבל חזרה קיבלנו מעגל!
תרגיל: יהי 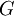 גרף פשוט (ללא לולאות וללא צלעות מקבילות) מסדר
גרף פשוט (ללא לולאות וללא צלעות מקבילות) מסדר 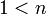 . הוכח שקיימים 2 קדקודים בעל אותה דרגה.
. הוכח שקיימים 2 קדקודים בעל אותה דרגה.
פתרון: נבנה פונקציה 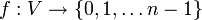 המוגדרת
המוגדרת 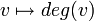 .
.
אם קיים קדקוד מדרגה n-1 אזי הוא מחובר לכולם ולכן אין קדקוד מדרגה אפס. במקרה זה נוכל להגדיר
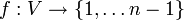 .
.
אם אין קדקוד כזה אז נוכל להגדיר 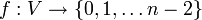 .
.
בשני המקרים קיבלנו כי 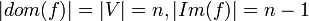 ולכן
ולכן  אינה חח"ע.
כלומר קיימים
אינה חח"ע.
כלומר קיימים 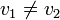 כך ש
כך ש 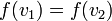 כלומר בעלי דרגה שווה
כלומר בעלי דרגה שווה
תרגיל: יהיה 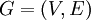 גרף פשוט עם 100 קדקודים כך שדרגת כל קדקוד לפחות 50. הוכח כי
גרף פשוט עם 100 קדקודים כך שדרגת כל קדקוד לפחות 50. הוכח כי 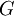 קשיר.
קשיר.
פתרון: יהיו 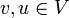 צריך להוכיח כי
צריך להוכיח כי ![[v]=[u]](/images/math/3/f/4/3f4e87b0feec5d1f15affa43926a02ce.png) (כך נסמן את רכיב הקשירות).
נניח כי הם שונים אזי ב
(כך נסמן את רכיב הקשירות).
נניח כי הם שונים אזי ב![|[v]|,|[u]|\geq 50](/images/math/e/d/1/ed1db6c064d6ea97ec9b899763a8f469.png) והם זרים. לכן
והם זרים. לכן ![[v]=[u]=50](/images/math/2/0/1/201ad8bc80e6600ee4eb670aae5435c2.png) אבל ברכיב קשירות שיש בו 50 קדקודים דרגת כל קדקוד קטנה שווה ל 49. סתירה
אבל ברכיב קשירות שיש בו 50 קדקודים דרגת כל קדקוד קטנה שווה ל 49. סתירה
תרגיל: יהי גרף לא מכוון 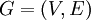 . הוכח כי אם
. הוכח כי אם 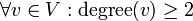 אז בגרף יש מעגל.
אז בגרף יש מעגל.
פתרון: בגרף יש יותר מ 2 קדקודים (אחרת לא יהיה להם 2 שכנים).
לפי משפט לחיצת הידיים מתקיים 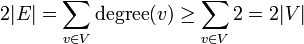 ולכן מספר הצלעות גדול שווה ממספר הקדקודים. לפי משפט קודם קיים מעגל בגרף.
ולכן מספר הצלעות גדול שווה ממספר הקדקודים. לפי משפט קודם קיים מעגל בגרף.
תרגיל: יהי גרף לא מכוון 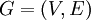 ללא מעגלים עם
ללא מעגלים עם 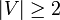 . הוכח כי קיימים
. הוכח כי קיימים 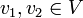 כך שדרגתם לכל היותר 1.
כך שדרגתם לכל היותר 1.
פתרון: לפי תרגיל קודם קיים 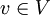 כך שדרגתו לכל היותר 1 (אחרת לכל הקדקודים יש דרגה לפחות 2 ואז יש מעגל לפי תרגיל קודם. סתירה!).
כך שדרגתו לכל היותר 1 (אחרת לכל הקדקודים יש דרגה לפחות 2 ואז יש מעגל לפי תרגיל קודם. סתירה!).
נמשיך באינדוקציה על  מספר הקדקודים בגרף.
מספר הקדקודים בגרף.
אם 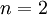 אזי או שהגרף הוא 2 נקודות לא צלעות או 2 נקודות המחוברות בצלע. בכל מקרה 2 הנקודות של הגרף הם מדרגה קטנה שווה ל-1.
אזי או שהגרף הוא 2 נקודות לא צלעות או 2 נקודות המחוברות בצלע. בכל מקרה 2 הנקודות של הגרף הם מדרגה קטנה שווה ל-1.
כעת נניח כי הטענה נכונה עבור 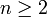 . נוכיח את הטענה עבור
. נוכיח את הטענה עבור 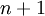 .
.
נבחר את הקדקוד 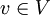 שדרגתו לכל היותר 1. נוריד אותו ואת הצלע שחלה בו אזי נקבל גרף עם
שדרגתו לכל היותר 1. נוריד אותו ואת הצלע שחלה בו אזי נקבל גרף עם  קדקודים. לפי הנחת האינדוקציה יש בו 2 קדקודים
קדקודים. לפי הנחת האינדוקציה יש בו 2 קדקודים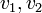 בעלי דרגה 1 לכל היותר. כעת נשוב לגרף המקורי (הכולל את
בעלי דרגה 1 לכל היותר. כעת נשוב לגרף המקורי (הכולל את 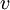 שהשמטנו).
שהשמטנו).
אם 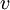 שכן של
שכן של 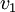 אזי
אזי 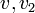 בעלי דרגה לכל היותר 1.
בעלי דרגה לכל היותר 1.
אם 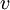 שכן של
שכן של 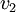 אזי
אזי 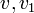 בעלי דרגה לכל היותר 1.
בעלי דרגה לכל היותר 1.
אם 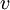 שכן של
שכן של 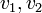 - סתירה כי הדרגה של
- סתירה כי הדרגה של 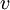 היא 1 לכל היותר.
היא 1 לכל היותר.
אם 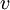 לא שכן של
לא שכן של 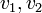 אזי
אזי 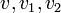 בעלי דרגה לכל היותר 1.
בעלי דרגה לכל היותר 1.
בכל מקרה קיבלנו כי קיימים 2 קדקודים בעלי דרגה 1 לכל היותר!.