משתמש:אור שחף/133 - הרצאה/22.3.11: הבדלים בין גרסאות בדף
מאין תקציר עריכה |
|||
| (גרסת ביניים אחת של אותו משתמש אינה מוצגת) | |||
| שורה 12: | שורה 12: | ||
=יישומים של אינטגרציה= | =יישומים של אינטגרציה= | ||
<ol> | <ol> | ||
<li>אם בקטע <math>[a,b]</math> מתקיים <math>f(x)\le g(x)</math> כבר ראינו שהשטח בין הגרפים הוא <math>\int\limits_a^b(g(x)-f(x))\mathrm dx</math>.</li> | <li> | ||
<li>נפח של גוף סיבוב | ==שטח== | ||
==דוגמאות== | אם בקטע <math>[a,b]</math> מתקיים <math>f(x)\le g(x)</math> כבר ראינו שהשטח בין הגרפים הוא <math>\int\limits_a^b(g(x)-f(x))\mathrm dx</math>.</li> | ||
<li> | |||
==נפח של גוף סיבוב== | |||
[[קובץ:נפח גוף סיבוב.png|ימין|ממוזער|250px]] | |||
נסובב את השטח מתחת לגרף <math>y=f(x)</math> בין a ל-b סביב ציר ה-x ונחשב את הנפח הנוצר. עבור <math>f(x)=c</math> קבוע הסיבוב יוצר גליל שנפחו ידוע לנו: <math>\pi c^2(b-a)</math>. כעת נניח ש-<math>f(x)\ge0</math> רציפה ב-<math>[a,b]</math> ונחשב את הנפח הנוצר ע"י סיבוב הגרף. נקח חלוקה כלשהי P של <math>[a,b]</math>, <math>a=x_0<x_1<x_2<\dots<x_n=b</math>. תחילה נעיין בנפח הנוצר כאשר אותו חלק מהגרף שמעל <math>[x_{k-1},x_k]</math> מסתובב סביב ציר ה-x. עפ"י המשפט השני של וירשטרס יש ל-f מקסימום <math>M_k</math> ומינימום <math>m_k</math> בקטע זה. נסמן ב-<math>V_k</math> הנפח שנוצר ע"י חלק זה של הגרף של f. אז מתקיים <math>\pi m_k^2(x_k-x_{x-1})\le V_k\le\pi M_k^2(x_k-x_{x-1})</math>. יוצא שהנפח בסה"כ הוא <math>V=\sum_{k=1}^n V_k</math> ומתקיים <math>\sum_{k=1}^n\pi m_k^2\Delta x_k\le V\le\sum_{k=1}^n\pi M_k^2\Delta x_k</math>. נשים לב שהסכום בצד ימין הוא בדיוק <math>\overline S(\pi f^2,P)</math> ובצד שמאל <math>\underline S(\pi f^2,P)</math> עבור החלוקה P. נשאיף <math>\lambda(P)\to0</math> וכיוון ש-f רציפה גם <math>\pi f^2</math> רציפה ולכן שני הסכומים הנ"ל שואפים לאותו הגבול: <math>V=\int\limits_a^b \pi f^2</math>. | |||
===דוגמאות=== | |||
# נחשב נפח של כדור בעל רדיוס r: {{left|<math>\begin{align}V&=\pi\int\limits_{-r}^r f^2\\&=\pi\int\limits_{-r}^r \left(r^2-x^2\right)\mathrm dx\\&=\pi\left[r^2x-\frac{x^3}3\right]_{x=-r}^r\\&=2\pi\left(r^3-\frac{r^3}3\right)\\&=\frac43\pi r^3\end{align}</math>}} {{משל}} | # נחשב נפח של כדור בעל רדיוס r: {{left|<math>\begin{align}V&=\pi\int\limits_{-r}^r f^2\\&=\pi\int\limits_{-r}^r \left(r^2-x^2\right)\mathrm dx\\&=\pi\left[r^2x-\frac{x^3}3\right]_{x=-r}^r\\&=2\pi\left(r^3-\frac{r^3}3\right)\\&=\frac43\pi r^3\end{align}</math>}} {{משל}} | ||
# נחשב נפח של חרוט בעל גובה h ורדיוס בסיס r. | # [[קובץ:נפח חרוט.png|ימין|ממוזער|300px]]נחשב נפח של חרוט בעל גובה h ורדיוס בסיס r. בסרטוט משמאל יש גרף סיבוב המתקבל מסיבוב משולש סביב ציר ה-x. הפונקציה היא <math>y=\frac rhx+0</math> ולפיכך הנפח הוא {{left|<math>\begin{align}V&=\pi\int\limits_0^h\left(\frac rhx\right)^2\mathrm dx\\&=\pi\left(\frac rh\right)^2\int\limits_0^h x^2\mathrm dx\\&=\pi\left(\frac rh\right)^2\left[\frac{x^3}3\right]_{x=0}^h\\&=\frac{\pi r^2h}3\end{align}</math>}}כלומר נפח החרוט הוא שליש מנפח הגליל בעל אותו גובה ורדיוס בסיסים. {{משל}} | ||
</li> | </li> | ||
<li>תהא f מוגדרת ורציפה ב-<math>[a,b]</math> ונחשב את הממוצע של f בקטע זה באופן הבא: לכל <math>n\in\mathbb N</math> נגדיר חלוקה <math>P_n</math> של הקטע לקטעים שווים <math>a=x_0<x_1<x_2<\dots<x_n=b</math>. כאשר <math>\forall k:\ x_k-x_{k-1}=\frac{b-a}n</math>. הממוצע של f בנקודות החלוקה הוא <math>\frac1n\sum_{k=1}^n f(x_k)</math>. לפי בחירת <math>P_n</math>, לכל k מתקיים <math>x_k-x_{k-1}=\frac{b-a}n\implies\frac1n=\frac{x_k-x_{k-1}}{b-a}</math> ונובע: <math>\sum_{k=1}^n\frac1n f(x_k)=\sum_{k=1}^nf(x_k)\frac{x_k-x_{k-1}}{b-a}=\frac1{b-a}\sum_{k=1}^n f(x_k)\Delta x_k</math> (כאשר <math>\sum_{k=1}^n f(x_k)\Delta x_k</math> הוא סכום רימן). נשאיף <math>n\to\infty</math> ומכיוון שבמקרה כזה <math>\lambda(P_n)\to0</math> מצאנו שהממוצע של f שואף ל-<math>\frac1{b-a}\int\limits_a^b f</math>. באותה דרך ניתן לחשב ממוצע של כל פונקציה אינטגרבילית, גם אם היא לא רציפה. ''גישה אחרת (אינטואיטיבית):'' אם <math>f(x)\ge0</math> רציפה אז <math>\frac1{b-a}\int\limits_a^b f</math> הוא השטח שמתחת לגרף חלקי אורך בסיס השטח, שזה הממוצע.</li> | <li> | ||
<li>אורך הגרף: עבור פונקציה f רציפה ב-<math>[a,b]</math> נעשה חלוקה <math>P_n</math> של הקטע. החלוקה גורמת לחלוקת הגרף ע"י נקודות <math>q_0,q_1,\dots,q_n</math>, כאשר לכל k <math>q_k=(x_k,f(x_k))</math>. קירוב סביר לאורך הגרף נתון ע"י <math>L(P)=\sum_{k=1}^n d(q_{k-1},q_k)</math>, כאשר <math>d(A,B)</math> הוא המרחק בין הנקודות A ו-B. מרחק זה שווה ל-<math>\sqrt{(x_{k-1}-x_k)^2+(f(x_k)-f(x_{k-1}))^2}</math>. לכן | ==ממוצע== | ||
תהא f מוגדרת ורציפה ב-<math>[a,b]</math> ונחשב את הממוצע של f בקטע זה באופן הבא: לכל <math>n\in\mathbb N</math> נגדיר חלוקה <math>P_n</math> של הקטע לקטעים שווים <math>a=x_0<x_1<x_2<\dots<x_n=b</math>. כאשר <math>\forall k:\ x_k-x_{k-1}=\frac{b-a}n</math>. הממוצע של f בנקודות החלוקה הוא <math>\frac1n\sum_{k=1}^n f(x_k)</math>. לפי בחירת <math>P_n</math>, לכל k מתקיים <math>x_k-x_{k-1}=\frac{b-a}n\implies\frac1n=\frac{x_k-x_{k-1}}{b-a}</math> ונובע: <math>\sum_{k=1}^n\frac1n f(x_k)=\sum_{k=1}^nf(x_k)\frac{x_k-x_{k-1}}{b-a}=\frac1{b-a}\sum_{k=1}^n f(x_k)\Delta x_k</math> (כאשר <math>\sum_{k=1}^n f(x_k)\Delta x_k</math> הוא סכום רימן). נשאיף <math>n\to\infty</math> ומכיוון שבמקרה כזה <math>\lambda(P_n)\to0</math> מצאנו שהממוצע של f שואף ל-<math>\frac1{b-a}\int\limits_a^b f</math>. באותה דרך ניתן לחשב ממוצע של כל פונקציה אינטגרבילית, גם אם היא לא רציפה. ''גישה אחרת (אינטואיטיבית):'' אם <math>f(x)\ge0</math> רציפה אז <math>\frac1{b-a}\int\limits_a^b f</math> הוא השטח שמתחת לגרף חלקי אורך בסיס השטח, שזה הממוצע.</li> | |||
<li> | |||
==אורך הגרף== | |||
[[קובץ:קירוב אורך גרף.png|ימין|300px]] | |||
עבור פונקציה f רציפה ב-<math>[a,b]</math> נעשה חלוקה <math>P_n</math> של הקטע. החלוקה גורמת לחלוקת הגרף ע"י נקודות <math>q_0,q_1,\dots,q_n</math>, כאשר לכל k <math>q_k=(x_k,f(x_k))</math>. קירוב סביר לאורך הגרף נתון ע"י <math>L(P)=\sum_{k=1}^n d(q_{k-1},q_k)</math>, כאשר <math>d(A,B)</math> הוא המרחק בין הנקודות A ו-B. מרחק זה שווה ל-<math>\sqrt{(x_{k-1}-x_k)^2+(f(x_k)-f(x_{k-1}))^2}</math>. לכן אורך הגרף L מקיים <math>\forall n:\ L(P_n)\le L</math> ואפשר להגדיר את L ע"י <math>L=\sup_n L(P_n)</math>. לפי זה L תמיד מוגדר <math>0<L\le\infty</math>.<br />''דוגמה:'' נגדיר <math>f(x)=\begin{cases}x\sin\left(\frac1x\right)&x\ne 0\\0&x=0\end{cases}</math>. היא רציפה בקטע הסגור <math>[0,1]</math> אבל אורך הגרף הוא <math>\infty</math>. | |||
נניח ש-{{ltr|f'}} קיימת ורציפה ב-<math>[a,b]</math> ונקח חלוקה P כלשהי. כבר ראינו ש-{{left|<math>\begin{align}L(P)&=\sum_{k=1}^n\sqrt{(x_{k-1}-x_k)^2+(f(x_k)-f(x_{k-1}))^2}\\&=\sum_{k=1}^n\sqrt{1+\left(\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}\right)^2}\ (x_k-x_{k-1})\\&=\sum_{k=1}^n\sqrt{1+f'(c_k)^2}\Delta x_k\end{align}</math>}}(ע"פ משפט לגראנז' יש <math>c_k</math> כאלה כך ש-<math>\forall k:\ c_k\in(x_{k-1},x_k)</math>) והגענו לסכום רימן עבור הפונקציה <math>\sqrt{1+f'(x)^2}</math>. היה נתון ש-<math>f'(x)</math> רציפה ולכן גם <math>\sqrt{1+f'(x)^2}</math> רציפה, וסכומי רימן אלה שואפים לאינטגרל <math>\int\limits_a^b\sqrt{1+f'(x)^2}\ \mathrm dx</math>. השערה מאוד סבירה היא שזהו אורך הגרף <math>L=\sup_n L(P_n)</math>. נוכיח זאת: נגדיר <math>I=\int\limits_a^b\sqrt{1+f'(x)^2}\mathrm dx</math> וכן <math>L=\sup_n L(P_n)</math> ונניח <math>L<\infty</math>. יהי <math>\varepsilon>0</math> נתון. לפי הגדרת הסופרימום קיימת חלוקה מסויימת Q של <math>[a,b]</math> כך ש-<math>0<L-L(Q)<\frac\varepsilon2</math>. אם {{ltr|Q'}} עידון של Q אז <math>L(Q)\le L(Q')\le L</math> ולכן <math>0\le L-L(Q')<\frac\varepsilon2</math>. כעת נתון ש-<math>f'</math> רציפה ולכן <math>\sqrt{1+f'(x)^2}</math> אינטגרבילית ב-<math>[a,b]</math>. לפיכך קיימת <math>\delta>0</math> כך שאם P חלוקה כלשהי של <math>[a,b]</math> כך ש-<math>\lambda(P)<\delta</math> ואם S סכום רימן כלשהו הבנוי על P אז <math>|I-S|<\frac\varepsilon2</math>. לבסוף נבחר P להיות עידון כלשהו של Q כך ש-<math>\lambda(P)<\delta</math>. כבר למדנו ש-<math>L(P)</math> הוא סכום רימן S עבור האינטגרל I שבנוי על P. מכל זה נסיק <math>|I-L|=|I-S+L(P)-L|\le|I-S|+|L(P)-L|<\varepsilon</math> ז"א I ו-L הם שני מספרים קבועים שהפרשם קטן מ-<math>\varepsilon</math> ומכאן נובע שהם שווים. {{משל}}</li> | |||
</ol> | </ol> | ||
גרסה אחרונה מ־14:35, 21 ביולי 2011
האינטגרל המסויים (המשך)
דוגמאות
- [math]\displaystyle{ \int\limits_0^2 x^2e^{x^3}\mathrm dx }[/math].
- שיטה א - נתעלם מהגבולות עד למציאת הפונקציה הקדומה: נציב [math]\displaystyle{ t=x^3\implies\frac{\mathrm dt}3=\mathrm dx }[/math]. לכן [math]\displaystyle{ \int=\int\frac{e^t}3\mathrm dt=\left[\frac{e^t}3\right]_{x=0}^2=\left[\frac{e^{x^3}}3\right]_{x=0}^2=\frac{e^8-1}3 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- דרך ב - נחליף את הגבולות במהלך החישוב: [math]\displaystyle{ t=x^3\implies t|_{x=0}=0,\ t|_{x=2}=8 }[/math] ולכן [math]\displaystyle{ \int=\int\limits_0^8\frac{e^t}3\mathrm dt=\left[\frac{e^t}3\right]_{t=0}^8=\frac{e^8-1}3 }[/math]. [math]\displaystyle{ \blacksquare }[/math]
- נחשב שטח עיגול בעל רדיוס r. [math]\displaystyle{ x^2+y^2=r^2\implies y=\sqrt{r^2-x^2} }[/math]. לכן השטח הוא [math]\displaystyle{ S=2\int\limits_{-r}^r\sqrt{r^2-x^2}\ \mathrm dx }[/math]. נציב [math]\displaystyle{ x=r\sin(\theta) }[/math] ואז [math]\displaystyle{ \begin{align}S&=2\int\limits_{-\frac\pi2}^{\frac\pi2}\sqrt{r^2-r^2\sin^2(\theta)}\ r\cos(\theta)\mathrm d\theta\\&=2\int\limits_{-\frac\pi2}^{\frac\pi2}r^2\cos^2(\theta)\mathrm d\theta\\&=2r^2\int\limits_{-\frac\pi2}^{\frac\pi2}\frac{\cos(2\theta)+1}2\mathrm d\theta\\&=2r^2\left[\frac{\frac12\sin(2\theta)+\theta}2\right]_{\theta=-\frac\pi2}^{\frac\pi2}\\&=2r^2\left(\frac14\cdot0+\frac\pi4-\frac14\cdot0+\frac\pi4\right)\\&=\pi r^2\end{align} }[/math][math]\displaystyle{ \blacksquare }[/math] הערה: כאשר החלפנו את גבולות האינטגרציה בהצגה [math]\displaystyle{ x=r\sin(\theta) }[/math] היינו צריכים לבחור [math]\displaystyle{ \theta }[/math] כך ש-[math]\displaystyle{ x=r }[/math], אבל עבור מעגל שרדיוסו r מתחלק ב-4 עם שארית 1 היינו יכולים לבחור גם [math]\displaystyle{ \theta=\frac{r\pi}2 }[/math] כי אז [math]\displaystyle{ x=r\sin(\theta)=r\sin\left(\frac{r\pi}2\right)=r }[/math], ועבור [math]\displaystyle{ x=-r }[/math] יכולנו לבחור [math]\displaystyle{ -\frac{r\pi}2 }[/math]. אם כן היינו מוצאים[math]\displaystyle{ \begin{align}S&=\int\limits_{-\frac{r\pi}2}^\frac{r\pi}2 \sqrt{r^2-r^2\sin^2(\theta)}\ r\cos(\theta)\mathrm d\theta\\&=2\int\limits_{-\frac{r\pi}2}^\frac{r\pi}2r^2\cos^2(\theta)\mathrm d\theta\\&=2r^2\int\limits_{-\frac{r\pi}2}^\frac{r\pi}2\frac{1+\cos(2\theta)}2\mathrm d\theta\\&=r\pi r^2\end{align} }[/math]הטעות נובעת מכך שקבענו ש-[math]\displaystyle{ \sqrt{r^2-r^2\sin^2(\theta)}=\sqrt{r^2\cos^2(\theta)}=r\cos(\theta) }[/math], מה שנכון רק כאשר [math]\displaystyle{ \cos(\theta)\ge0 }[/math]. הטווח של האינטגרציה היה [math]\displaystyle{ \left[-\frac{r\pi}2,\frac{r\pi}2\right] }[/math], שכולל תחומים בהם [math]\displaystyle{ \cos(\theta)\lt 0 }[/math]. בתחומים אלה צריך לבחור [math]\displaystyle{ \sqrt{r^2\cos^2(\theta)}=-r\cos(\theta) }[/math] ולחלק את הקטע [math]\displaystyle{ \left[-\frac{r\pi}2,\frac{r\pi}2\right] }[/math] לתחומים שונים לפי הסימן של [math]\displaystyle{ \cos(\theta) }[/math].
יישומים של אינטגרציה
-
שטח
אם בקטע [math]\displaystyle{ [a,b] }[/math] מתקיים [math]\displaystyle{ f(x)\le g(x) }[/math] כבר ראינו שהשטח בין הגרפים הוא [math]\displaystyle{ \int\limits_a^b(g(x)-f(x))\mathrm dx }[/math]. -
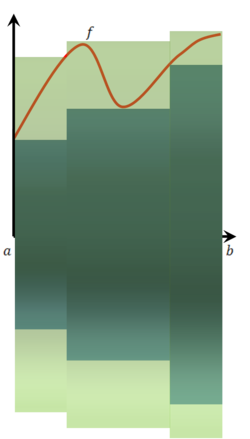
נפח של גוף סיבוב
נסובב את השטח מתחת לגרף [math]\displaystyle{ y=f(x) }[/math] בין a ל-b סביב ציר ה-x ונחשב את הנפח הנוצר. עבור [math]\displaystyle{ f(x)=c }[/math] קבוע הסיבוב יוצר גליל שנפחו ידוע לנו: [math]\displaystyle{ \pi c^2(b-a) }[/math]. כעת נניח ש-[math]\displaystyle{ f(x)\ge0 }[/math] רציפה ב-[math]\displaystyle{ [a,b] }[/math] ונחשב את הנפח הנוצר ע"י סיבוב הגרף. נקח חלוקה כלשהי P של [math]\displaystyle{ [a,b] }[/math], [math]\displaystyle{ a=x_0\lt x_1\lt x_2\lt \dots\lt x_n=b }[/math]. תחילה נעיין בנפח הנוצר כאשר אותו חלק מהגרף שמעל [math]\displaystyle{ [x_{k-1},x_k] }[/math] מסתובב סביב ציר ה-x. עפ"י המשפט השני של וירשטרס יש ל-f מקסימום [math]\displaystyle{ M_k }[/math] ומינימום [math]\displaystyle{ m_k }[/math] בקטע זה. נסמן ב-[math]\displaystyle{ V_k }[/math] הנפח שנוצר ע"י חלק זה של הגרף של f. אז מתקיים [math]\displaystyle{ \pi m_k^2(x_k-x_{x-1})\le V_k\le\pi M_k^2(x_k-x_{x-1}) }[/math]. יוצא שהנפח בסה"כ הוא [math]\displaystyle{ V=\sum_{k=1}^n V_k }[/math] ומתקיים [math]\displaystyle{ \sum_{k=1}^n\pi m_k^2\Delta x_k\le V\le\sum_{k=1}^n\pi M_k^2\Delta x_k }[/math]. נשים לב שהסכום בצד ימין הוא בדיוק [math]\displaystyle{ \overline S(\pi f^2,P) }[/math] ובצד שמאל [math]\displaystyle{ \underline S(\pi f^2,P) }[/math] עבור החלוקה P. נשאיף [math]\displaystyle{ \lambda(P)\to0 }[/math] וכיוון ש-f רציפה גם [math]\displaystyle{ \pi f^2 }[/math] רציפה ולכן שני הסכומים הנ"ל שואפים לאותו הגבול: [math]\displaystyle{ V=\int\limits_a^b \pi f^2 }[/math].
דוגמאות
- נחשב נפח של כדור בעל רדיוס r: [math]\displaystyle{ \begin{align}V&=\pi\int\limits_{-r}^r f^2\\&=\pi\int\limits_{-r}^r \left(r^2-x^2\right)\mathrm dx\\&=\pi\left[r^2x-\frac{x^3}3\right]_{x=-r}^r\\&=2\pi\left(r^3-\frac{r^3}3\right)\\&=\frac43\pi r^3\end{align} }[/math][math]\displaystyle{ \blacksquare }[/math]
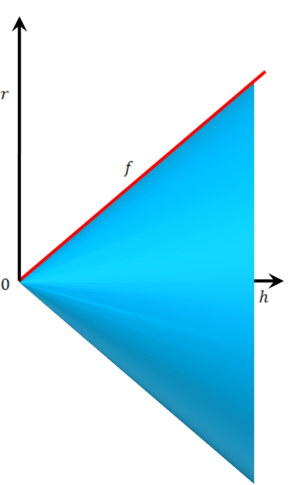
- נחשב נפח של חרוט בעל גובה h ורדיוס בסיס r. בסרטוט משמאל יש גרף סיבוב המתקבל מסיבוב משולש סביב ציר ה-x. הפונקציה היא [math]\displaystyle{ y=\frac rhx+0 }[/math] ולפיכך הנפח הוא [math]\displaystyle{ \begin{align}V&=\pi\int\limits_0^h\left(\frac rhx\right)^2\mathrm dx\\&=\pi\left(\frac rh\right)^2\int\limits_0^h x^2\mathrm dx\\&=\pi\left(\frac rh\right)^2\left[\frac{x^3}3\right]_{x=0}^h\\&=\frac{\pi r^2h}3\end{align} }[/math]כלומר נפח החרוט הוא שליש מנפח הגליל בעל אותו גובה ורדיוס בסיסים. [math]\displaystyle{ \blacksquare }[/math]
- נחשב נפח של כדור בעל רדיוס r:
-
ממוצע
תהא f מוגדרת ורציפה ב-[math]\displaystyle{ [a,b] }[/math] ונחשב את הממוצע של f בקטע זה באופן הבא: לכל [math]\displaystyle{ n\in\mathbb N }[/math] נגדיר חלוקה [math]\displaystyle{ P_n }[/math] של הקטע לקטעים שווים [math]\displaystyle{ a=x_0\lt x_1\lt x_2\lt \dots\lt x_n=b }[/math]. כאשר [math]\displaystyle{ \forall k:\ x_k-x_{k-1}=\frac{b-a}n }[/math]. הממוצע של f בנקודות החלוקה הוא [math]\displaystyle{ \frac1n\sum_{k=1}^n f(x_k) }[/math]. לפי בחירת [math]\displaystyle{ P_n }[/math], לכל k מתקיים [math]\displaystyle{ x_k-x_{k-1}=\frac{b-a}n\implies\frac1n=\frac{x_k-x_{k-1}}{b-a} }[/math] ונובע: [math]\displaystyle{ \sum_{k=1}^n\frac1n f(x_k)=\sum_{k=1}^nf(x_k)\frac{x_k-x_{k-1}}{b-a}=\frac1{b-a}\sum_{k=1}^n f(x_k)\Delta x_k }[/math] (כאשר [math]\displaystyle{ \sum_{k=1}^n f(x_k)\Delta x_k }[/math] הוא סכום רימן). נשאיף [math]\displaystyle{ n\to\infty }[/math] ומכיוון שבמקרה כזה [math]\displaystyle{ \lambda(P_n)\to0 }[/math] מצאנו שהממוצע של f שואף ל-[math]\displaystyle{ \frac1{b-a}\int\limits_a^b f }[/math]. באותה דרך ניתן לחשב ממוצע של כל פונקציה אינטגרבילית, גם אם היא לא רציפה. גישה אחרת (אינטואיטיבית): אם [math]\displaystyle{ f(x)\ge0 }[/math] רציפה אז [math]\displaystyle{ \frac1{b-a}\int\limits_a^b f }[/math] הוא השטח שמתחת לגרף חלקי אורך בסיס השטח, שזה הממוצע. -
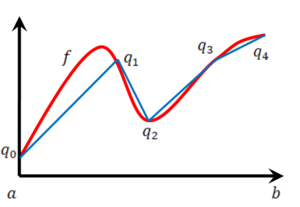
אורך הגרף
עבור פונקציה f רציפה ב-[math]\displaystyle{ [a,b] }[/math] נעשה חלוקה [math]\displaystyle{ P_n }[/math] של הקטע. החלוקה גורמת לחלוקת הגרף ע"י נקודות [math]\displaystyle{ q_0,q_1,\dots,q_n }[/math], כאשר לכל k [math]\displaystyle{ q_k=(x_k,f(x_k)) }[/math]. קירוב סביר לאורך הגרף נתון ע"י [math]\displaystyle{ L(P)=\sum_{k=1}^n d(q_{k-1},q_k) }[/math], כאשר [math]\displaystyle{ d(A,B) }[/math] הוא המרחק בין הנקודות A ו-B. מרחק זה שווה ל-[math]\displaystyle{ \sqrt{(x_{k-1}-x_k)^2+(f(x_k)-f(x_{k-1}))^2} }[/math]. לכן אורך הגרף L מקיים [math]\displaystyle{ \forall n:\ L(P_n)\le L }[/math] ואפשר להגדיר את L ע"י [math]\displaystyle{ L=\sup_n L(P_n) }[/math]. לפי זה L תמיד מוגדר [math]\displaystyle{ 0\lt L\le\infty }[/math].
נניח ש-f' קיימת ורציפה ב-[math]\displaystyle{ [a,b] }[/math] ונקח חלוקה P כלשהי. כבר ראינו ש-
דוגמה: נגדיר [math]\displaystyle{ f(x)=\begin{cases}x\sin\left(\frac1x\right)&x\ne 0\\0&x=0\end{cases} }[/math]. היא רציפה בקטע הסגור [math]\displaystyle{ [0,1] }[/math] אבל אורך הגרף הוא [math]\displaystyle{ \infty }[/math].[math]\displaystyle{ \begin{align}L(P)&=\sum_{k=1}^n\sqrt{(x_{k-1}-x_k)^2+(f(x_k)-f(x_{k-1}))^2}\\&=\sum_{k=1}^n\sqrt{1+\left(\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}\right)^2}\ (x_k-x_{k-1})\\&=\sum_{k=1}^n\sqrt{1+f'(c_k)^2}\Delta x_k\end{align} }[/math](ע"פ משפט לגראנז' יש [math]\displaystyle{ c_k }[/math] כאלה כך ש-[math]\displaystyle{ \forall k:\ c_k\in(x_{k-1},x_k) }[/math]) והגענו לסכום רימן עבור הפונקציה [math]\displaystyle{ \sqrt{1+f'(x)^2} }[/math]. היה נתון ש-[math]\displaystyle{ f'(x) }[/math] רציפה ולכן גם [math]\displaystyle{ \sqrt{1+f'(x)^2} }[/math] רציפה, וסכומי רימן אלה שואפים לאינטגרל [math]\displaystyle{ \int\limits_a^b\sqrt{1+f'(x)^2}\ \mathrm dx }[/math]. השערה מאוד סבירה היא שזהו אורך הגרף [math]\displaystyle{ L=\sup_n L(P_n) }[/math]. נוכיח זאת: נגדיר [math]\displaystyle{ I=\int\limits_a^b\sqrt{1+f'(x)^2}\mathrm dx }[/math] וכן [math]\displaystyle{ L=\sup_n L(P_n) }[/math] ונניח [math]\displaystyle{ L\lt \infty }[/math]. יהי [math]\displaystyle{ \varepsilon\gt 0 }[/math] נתון. לפי הגדרת הסופרימום קיימת חלוקה מסויימת Q של [math]\displaystyle{ [a,b] }[/math] כך ש-[math]\displaystyle{ 0\lt L-L(Q)\lt \frac\varepsilon2 }[/math]. אם Q' עידון של Q אז [math]\displaystyle{ L(Q)\le L(Q')\le L }[/math] ולכן [math]\displaystyle{ 0\le L-L(Q')\lt \frac\varepsilon2 }[/math]. כעת נתון ש-[math]\displaystyle{ f' }[/math] רציפה ולכן [math]\displaystyle{ \sqrt{1+f'(x)^2} }[/math] אינטגרבילית ב-[math]\displaystyle{ [a,b] }[/math]. לפיכך קיימת [math]\displaystyle{ \delta\gt 0 }[/math] כך שאם P חלוקה כלשהי של [math]\displaystyle{ [a,b] }[/math] כך ש-[math]\displaystyle{ \lambda(P)\lt \delta }[/math] ואם S סכום רימן כלשהו הבנוי על P אז [math]\displaystyle{ |I-S|\lt \frac\varepsilon2 }[/math]. לבסוף נבחר P להיות עידון כלשהו של Q כך ש-[math]\displaystyle{ \lambda(P)\lt \delta }[/math]. כבר למדנו ש-[math]\displaystyle{ L(P) }[/math] הוא סכום רימן S עבור האינטגרל I שבנוי על P. מכל זה נסיק [math]\displaystyle{ |I-L|=|I-S+L(P)-L|\le|I-S|+|L(P)-L|\lt \varepsilon }[/math] ז"א I ו-L הם שני מספרים קבועים שהפרשם קטן מ-[math]\displaystyle{ \varepsilon }[/math] ומכאן נובע שהם שווים. [math]\displaystyle{ \blacksquare }[/math]