הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 3"
(←יחסי סדר) |
(←יחסי סדר) |
||
| שורה 19: | שורה 19: | ||
הערה: קל להוכיח מתוך תכונת האנטי-סימטריות שאם קיים איבר מינימום הוא יחיד (למרות שהוא לא חייב להיות קיים), ונכון הדבר לגבי המקסימום. | הערה: קל להוכיח מתוך תכונת האנטי-סימטריות שאם קיים איבר מינימום הוא יחיד (למרות שהוא לא חייב להיות קיים), ונכון הדבר לגבי המקסימום. | ||
| + | |||
| + | |||
| + | '''דוגמא.''' | ||
| + | |||
| + | נביט בקבוצה <math>A=\{1,2,3,4,5\}</math> ונגדיר עליה יחס סדר חלקי: | ||
| + | |||
| + | <math>R=\{(1,1),(2,2),(3,3),(4,4),(5,5),(2,4),(1,2),(1,4),(3,2),(3,4),(5,2),(5,4)\}</math> | ||
| + | |||
| + | (הזוגיים 'גדולים' מכל אי הזוגיים ומהזוגיים הקטנים מהם) | ||
| + | |||
| + | *5,3,1 הינם איברים מינימליים שכן אין איבר שקטן מאף אחד מהם. הם אינם מינימום כי אף אחד מהם לא קטן מכל האיברים האחרים. | ||
| + | *4 הינו מקסימום של הקבוצה, הוא בוודאי מקסימלי | ||
| + | *2 קטן מחלק מהאיברים וגדול מאחרים לכן הוא כלום. | ||
| שורה 41: | שורה 54: | ||
'''דוגמא.''' | '''דוגמא.''' | ||
| − | נביט | + | נשוב לדוגמא הקודמת. נביט בתת הקבוצה המכילה את המספרים האי זוגיים בלבד <math>B=\{1,3,5\}</math>. קבוצת חסמי המלעיל של B הינה <math>\{2,4\}</math>. המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון. |
| − | + | ||
| − | <math> | + | |
| − | + | ||
| − | + | ||
גרסה מ־14:24, 30 ביולי 2011
יחסי סדר
הגדרה: יחס R על A נקרא אנטי-סימטרי אם מתקיים ![\forall x,y\in A:[(x,y)\in R]\and[(y,x)\in R] \rightarrow (x=y)](/images/math/b/2/7/b27500f5e820926a1e38f94ccc781069.png)
כלומר, אם 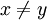 אז לא יכול להיות שמתקיים היחס בין x לבין y וגם היחס בין y לx.
אז לא יכול להיות שמתקיים היחס בין x לבין y וגם היחס בין y לx.
הגדרה: יחס R על A נקרא יחס סדר חלקי אם R רפלקסיבי, טרנזיטיבי ואנטי-סימטרי
דוגמאות ליחסי סדר חלקי:
- היחס 'קטן-שווה' על המספרים
- היחס 'מוכל-שווה' על הקבוצות
הגדרה: דיאגרמת הסה Hassse
הגדרות. יהיו A קבוצה וR יחס סדר חלקי על הקבוצה:
- איבר
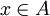 נקרא מינמלי ביחס לR אם
נקרא מינמלי ביחס לR אם 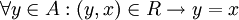 . כלומר, אין איבר 'קטן' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו.
. כלומר, אין איבר 'קטן' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו. - איבר
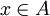 נקרא מקסימלי ביחס לR אם
נקרא מקסימלי ביחס לR אם 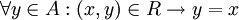 . כלומר, אין איבר 'גדול' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו.
. כלומר, אין איבר 'גדול' מx. לא חייב להתקיים ש-x ביחס כלשהו עם איבר כלשהו. - איבר
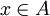 נקרא מינימום ביחס לR אם
נקרא מינימום ביחס לR אם 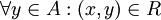 . כלומר, x 'קטן' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה הריקה תחת יחס הכלה)
. כלומר, x 'קטן' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה הריקה תחת יחס הכלה) - איבר
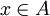 נקרא מקסימום ביחס לR אם
נקרא מקסימום ביחס לR אם 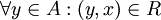 . כלומר, x 'גדול' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה B תחת יחס ההכלה על קבוצת החזקה של B)
. כלומר, x 'גדול' מכל האיברים. x חייב להיות ביחס עם כל האיברים בקבוצה. (דוגמא: הקבוצה B תחת יחס ההכלה על קבוצת החזקה של B)
הערה: קל להוכיח מתוך תכונת האנטי-סימטריות שאם קיים איבר מינימום הוא יחיד (למרות שהוא לא חייב להיות קיים), ונכון הדבר לגבי המקסימום.
דוגמא.
נביט בקבוצה 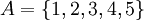 ונגדיר עליה יחס סדר חלקי:
ונגדיר עליה יחס סדר חלקי:
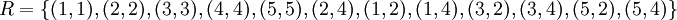
(הזוגיים 'גדולים' מכל אי הזוגיים ומהזוגיים הקטנים מהם)
- 5,3,1 הינם איברים מינימליים שכן אין איבר שקטן מאף אחד מהם. הם אינם מינימום כי אף אחד מהם לא קטן מכל האיברים האחרים.
- 4 הינו מקסימום של הקבוצה, הוא בוודאי מקסימלי
- 2 קטן מחלק מהאיברים וגדול מאחרים לכן הוא כלום.
הגדרה: יהי R יחס על A, אזי היחס ההופכי מוגדר להיות 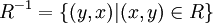
תרגיל.
הוכח שאם R יחס סדר חלקי, גם ההופכי שלו יחס סדר חלקי
פתרון.
- רפלקסיביות: לכל איבר a מתקיים
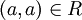 ולכן
ולכן 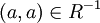
- טרנזיטיביות: נניח
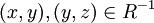 לכן מתקיים
לכן מתקיים 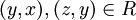 לכן לפי הטרנזיטיביות של R מתקיים
לכן לפי הטרנזיטיביות של R מתקיים 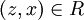 ולכן
ולכן 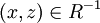 .
. - אנטי-סימטריות: אם x ביחס לy וגם y ביחס לx הדבר נכון באופן זהה לR ולהופכי שלו, ולכן x=y.
הגדרות. יהיו A קבוצה, B קבוצה המוכלת בה וR יחס סדר חלקי:
- חסם מלעיל של B הוא איבר
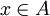 כך שמתקיים
כך שמתקיים 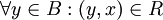
- חסם מלרע של B הוא איבר
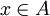 כך שמתקיים
כך שמתקיים 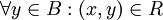
- החסם העליון (סופרמום) של B הינו המינימום של קבוצת חסמי המלעיל (אם קיים). מסומן
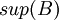
- החסם התחתון (אינפימום) של B הינו המקסימום של קבוצת חסמי המלרע (אם קיים). מסומן
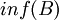
דוגמא.
נשוב לדוגמא הקודמת. נביט בתת הקבוצה המכילה את המספרים האי זוגיים בלבד 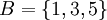 . קבוצת חסמי המלעיל של B הינה
. קבוצת חסמי המלעיל של B הינה 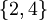 . המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.
. המינימום של קבוצה זו הוא 2 ולכן הוא החסם העליון של B. אין חסם מלרע ל-B ולכן בוודאי אין לה חסם תחתון.