הבדלים בין גרסאות בדף "אינטגרל לא מסויים/דוגמאות"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏3)
שורה 3: שורה 3:
  
 
==2==
 
==2==
 +
 
<math>\int \frac{dx}{\sqrt{x^{2}-4x-5}}</math>
 
<math>\int \frac{dx}{\sqrt{x^{2}-4x-5}}</math>
  
 +
===פתרון===
  
 
'''השלמה לריבוע והצבה ראשונה:'''
 
'''השלמה לריבוע והצבה ראשונה:'''
שורה 38: שורה 40:
 
האינטגרל הבא לקוח מספר התרגילים של בועז צבאן (1.24, אם אינני טועה)
 
האינטגרל הבא לקוח מספר התרגילים של בועז צבאן (1.24, אם אינני טועה)
  
 +
<math>\int \frac{sin^{2}(x)}{cos^{6}(x)}dx</math>
 +
 +
===פתרון===
 
<math>\int \frac{sin^{2}(x)}{cos^{6}(x)}dx=\begin{Bmatrix}
 
<math>\int \frac{sin^{2}(x)}{cos^{6}(x)}dx=\begin{Bmatrix}
 
t=tanx\\  
 
t=tanx\\  
שורה 50: שורה 55:
 
<math>\int \frac{sin^{2}(x)}{cos^{6}(x)}dx
 
<math>\int \frac{sin^{2}(x)}{cos^{6}(x)}dx
 
=\int \frac{\frac{t^{2}}{t^{2}+1}}{\frac{1}{(t^2+1)^{2}}}dt=\int t^{2}(t^{2}+1)dt=\cdots =\frac{t^{5}}{5}+\frac{t^{3}}{3}+c</math>
 
=\int \frac{\frac{t^{2}}{t^{2}+1}}{\frac{1}{(t^2+1)^{2}}}dt=\int t^{2}(t^{2}+1)dt=\cdots =\frac{t^{5}}{5}+\frac{t^{3}}{3}+c</math>
 +
 +
==4==
 +
 +
בדומה לאינטגרל הקודם, לקוח מבועז צבאן (1.27)
 +
 +
<math>\int \sqrt{2-x-x^{2}}dx</math>
 +
 +
===דרך א'===
 +
 +
'''א.''' ניתן להשתמש בהצבת אויילר, אבל אנחנו ננקוט בטקטיקה שונה.
 +
 +
<math>\int \sqrt{2-x-x^{2}}dx=\int \sqrt{1.5^{2}-(x+0.5)^{2}}dx=\int \sqrt{1.5^{2}-u^{2}}du</math>
 +
 +
 +
הצבה ראשונה: <math>u=x+0.5\Rightarrow dx=du</math>
 +
 +
 +
הצבה שנייה: <math>u=1.5sint\Rightarrow du=1.5costdt</math>
 +
 +
 +
ואם נחזור לחישוב האינטגרל,
 +
 +
<math>\int \sqrt{1.5^{2}-u^{2}}du=\int 1.5\sqrt{1-sin^{2}(t)} \cdot 1.5cos(t)dt=2.25\int cos^{2}(t)dt=2.25\int\frac{cos2t-1}{2}dt=2.25(\frac{sin2t}{4}-\frac{t}{2})+c </math>
 +
 +
ומכאן מעבירים את t לx.
 +
 +
===דרך ב'===
 +
 +
ההצבה הראשונה נשארת כפי שהייתה, אך הפעם לא נעשה הצבה שניה אלא נשתמש באינטגרציה בחלקים:
 +
 +
<math>\int \sqrt{1.5^{2}-u^{2}}du=\int (u)'\sqrt{1.5^{2}-u^{2}}du=u\sqrt{1.5^{2}-u^{2}}+\int \frac{u^{2}du}{\sqrt{1.5^{2}-u^{2}}}</math>
 +
 +
 +
כעת נוכל להבחין כי מתקיים:
 +
 +
 +
<math>\int \frac{u^{2}du}{\sqrt{1.5^{2}-u^{2}}}=\int \frac{u^{2}-1.5^{2}+1.5^{2}}{\sqrt{1.5^{2}-u^{2}}}du=\int\frac{1.5^{2}}{\sqrt{1.5^{2}-u^{2}}}du-\int\sqrt{1.5^{2}-u^{2}}du  </math>
 +
 +
 +
כעת נביט רק על האינטגרל הראשון ונציב:  <math>1.5v=u</math>
 +
 +
<math>\int\frac{1.5^{2}}{\sqrt{1.5^{2}-u^{2}}}du=1.5^{2}\int \frac{1.5dv}{1.5\sqrt{1-v^{2}}}=1.5^{2}arcsin(v)=2.25arcsin(\frac{2u}{3}) </math>
 +
 +
אם נחזור לאינטגרל המקורי נקבל:
 +
 +
<math>\int \sqrt{1.5^{2}-u^{2}}du=u\sqrt{1.5^{2}-u^{2}}+2.25arcsin(\frac{2u}{3})-\int \sqrt{1.5^{2}-u^{2}}du </math>
 +
 +
<math>2\int \sqrt{1.5^{2}-u^{2}}du=u\sqrt{1.5^{2}-u^{2}}+2.25arcsin(\frac{2u}{3})</math>
 +
 +
וסיימנו (:

גרסה מ־07:39, 29 באפריל 2012

1

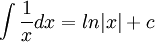
\int \frac{1}{x} dx = ln|x|+c

2

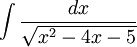
\int \frac{dx}{\sqrt{x^{2}-4x-5}}

פתרון

השלמה לריבוע והצבה ראשונה:

הדבר הראשון שנעשה הוא התהליך של השלמה לריבוע, שבסופו נקבל כי:

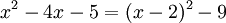
x^{2}-4x-5=(x-2)^{2}-9

ולכן ההצבה הראשונה שנעשה תהא: 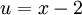u=x-2, וכמובן קל להבין כי dx=du.

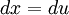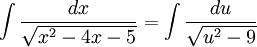
\int \frac{dx}{\sqrt{x^{2}-4x-5}}=\int \frac{du}{\sqrt{u^{2}-9}}


פונקציות טריגונומטריות היפרבוליות (הערה):

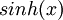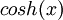ניעזר בתכונות של sinh(x) ושל cosh(x):

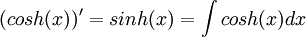
(cosh(x))'=sinh(x)=\int cosh(x)dx

וכן בזהות: 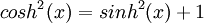cosh^{2}(x)=sinh^{2}(x)+1


הצבה שנייה:

נציב: 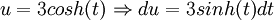u=3cosh(t)\Rightarrow du=3sinh(t)dt

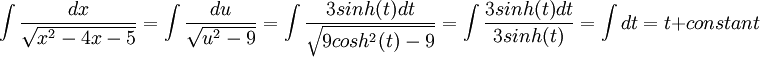
\int \frac{dx}{\sqrt{x^{2}-4x-5}}=\int \frac{du}{\sqrt{u^{2}-9}}=\int \frac{3sinh(t)dt}{\sqrt{9cosh^{2}(t)-9}}=\int \frac{3sinh(t)dt}{3sinh(t)}=\int dt=t+constant

ולהחזיר את t לx, אני משאיר לכם (:

3

האינטגרל הבא לקוח מספר התרגילים של בועז צבאן (1.24, אם אינני טועה)

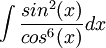
\int \frac{sin^{2}(x)}{cos^{6}(x)}dx

פתרון

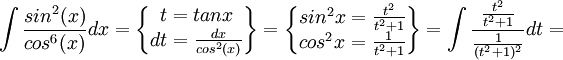
\int \frac{sin^{2}(x)}{cos^{6}(x)}dx=\begin{Bmatrix} t=tanx\\ dt=\frac{dx}{cos^{2}(x)} \end{Bmatrix} =\begin{Bmatrix} sin^{2}x=\frac{t^{2}}{t^{2}+1}\\ cos^{2}x=\frac{1}{t^{2}+1} \end{Bmatrix} =\int \frac{\frac{t^{2}}{t^{2}+1}}{\frac{1}{(t^2+1)^{2}}}dt=

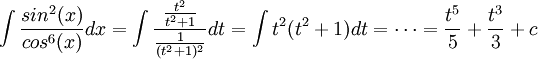
\int \frac{sin^{2}(x)}{cos^{6}(x)}dx =\int \frac{\frac{t^{2}}{t^{2}+1}}{\frac{1}{(t^2+1)^{2}}}dt=\int t^{2}(t^{2}+1)dt=\cdots =\frac{t^{5}}{5}+\frac{t^{3}}{3}+c

4

בדומה לאינטגרל הקודם, לקוח מבועז צבאן (1.27)

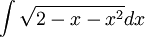
\int \sqrt{2-x-x^{2}}dx

דרך א'

א. ניתן להשתמש בהצבת אויילר, אבל אנחנו ננקוט בטקטיקה שונה.

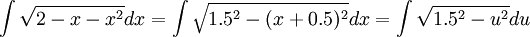
\int \sqrt{2-x-x^{2}}dx=\int \sqrt{1.5^{2}-(x+0.5)^{2}}dx=\int \sqrt{1.5^{2}-u^{2}}du


הצבה ראשונה: 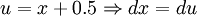u=x+0.5\Rightarrow dx=du


הצבה שנייה: 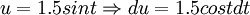u=1.5sint\Rightarrow du=1.5costdt


ואם נחזור לחישוב האינטגרל,

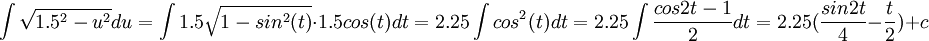
\int \sqrt{1.5^{2}-u^{2}}du=\int 1.5\sqrt{1-sin^{2}(t)} \cdot 1.5cos(t)dt=2.25\int cos^{2}(t)dt=2.25\int\frac{cos2t-1}{2}dt=2.25(\frac{sin2t}{4}-\frac{t}{2})+c

ומכאן מעבירים את t לx.

דרך ב'

ההצבה הראשונה נשארת כפי שהייתה, אך הפעם לא נעשה הצבה שניה אלא נשתמש באינטגרציה בחלקים:

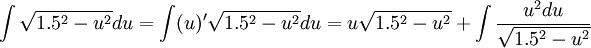
\int \sqrt{1.5^{2}-u^{2}}du=\int (u)'\sqrt{1.5^{2}-u^{2}}du=u\sqrt{1.5^{2}-u^{2}}+\int \frac{u^{2}du}{\sqrt{1.5^{2}-u^{2}}}


כעת נוכל להבחין כי מתקיים:


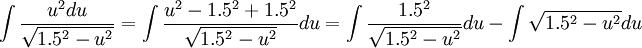
\int \frac{u^{2}du}{\sqrt{1.5^{2}-u^{2}}}=\int \frac{u^{2}-1.5^{2}+1.5^{2}}{\sqrt{1.5^{2}-u^{2}}}du=\int\frac{1.5^{2}}{\sqrt{1.5^{2}-u^{2}}}du-\int\sqrt{1.5^{2}-u^{2}}du


כעת נביט רק על האינטגרל הראשון ונציב: 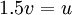1.5v=u

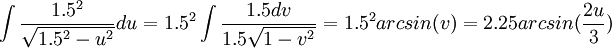
\int\frac{1.5^{2}}{\sqrt{1.5^{2}-u^{2}}}du=1.5^{2}\int \frac{1.5dv}{1.5\sqrt{1-v^{2}}}=1.5^{2}arcsin(v)=2.25arcsin(\frac{2u}{3})

אם נחזור לאינטגרל המקורי נקבל:

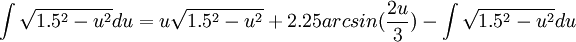
\int \sqrt{1.5^{2}-u^{2}}du=u\sqrt{1.5^{2}-u^{2}}+2.25arcsin(\frac{2u}{3})-\int \sqrt{1.5^{2}-u^{2}}du

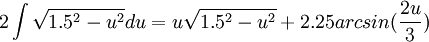
2\int \sqrt{1.5^{2}-u^{2}}du=u\sqrt{1.5^{2}-u^{2}}+2.25arcsin(\frac{2u}{3})

וסיימנו (:

מקור: https://math-wiki.com/index.php?title=אינטגרל_לא_מסויים/דוגמאות&oldid=22119