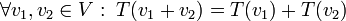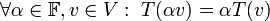הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/8"
אחיה בר-און (שיחה | תרומות) (←דוגמאות ודוגמאות נגדיות) |
אחיה בר-און (שיחה | תרומות) (←דוגמאות) |
||
| שורה 48: | שורה 48: | ||
6. יהי <math>V</math> מ"ו מעל <math>\mathbb{F}</math> מימד <math>n</math> ויהי <math>B</math> בסיס אזי הפונקציה <math>T:V\to \mathbb{F}^n</math> | 6. יהי <math>V</math> מ"ו מעל <math>\mathbb{F}</math> מימד <math>n</math> ויהי <math>B</math> בסיס אזי הפונקציה <math>T:V\to \mathbb{F}^n</math> | ||
המוגדרת <math>v\mapsto [v]_B</math> היא ה"ל. | המוגדרת <math>v\mapsto [v]_B</math> היא ה"ל. | ||
| + | |||
| + | == תרגיל == | ||
| + | יהיו <math>T,S:V\to W</math> שתי ה"ל. <math>B=\{v_{1},\dots,v_{n}\}</math> בסיס ל <math>V</math>. נניח <math>T(v_{i})=S(v_{i})</math> לכל <math>1\leq i\leq n</math> | ||
| + | |||
| + | הוכח: <math>T=S</math>. כלומר לכל <math>v\in V</math> מתקיים <math>T(v)=S(v)</math> | ||
| + | |||
| + | הוכחה: יהי <math>v\in V</math> אזי <math>v=\sum\limits _{i=1}^{n}\alpha_{i}v_{i}</math> כי <math>B</math> בסיס ובפרט פורשת. | ||
| + | ואז | ||
| + | |||
| + | <math> | ||
| + | T(v)=T(\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots+\alpha_{n}v_{n})=\alpha_{1}T(v_{1})+\alpha_{2}T(v_{2})+\cdots+\alpha_{n}T(v_{n}) = \\ | ||
| + | = \alpha_{1}S(v_{1})+\alpha_{2}S(v_{2})+\cdots+\alpha_{n}S(v_{n})=S(\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots+\alpha_{n}v_{n})=S(v) | ||
| + | </math> | ||
גרסה מ־15:04, 19 ביולי 2015
העתקות לינאריות (ה"ל)
הגדרה: יהיו 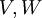 שני מ"ו מעל אותו שדה
שני מ"ו מעל אותו שדה 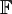 . ה"ל היא פונקציה
. ה"ל היא פונקציה 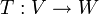 אם
אם
(או באופן שקול: אם לכל 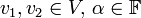 מתקיים
מתקיים 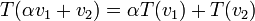 )
)
תכונות בסיסיות:
.1 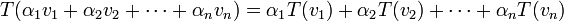
.2 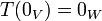
דוגמאות
1. יהיו 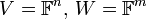 שניהם מעל
שניהם מעל 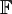 . תהא
. תהא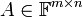 אזי העתקה
אזי העתקה 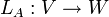 המוגדרת
המוגדרת  היא ה"ל.
היא ה"ל.
הוכחה: לכל 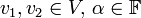 מתקיים
מתקיים
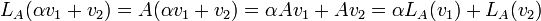
2.  שניהם מעל
שניהם מעל 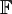 . אזי העתקה
. אזי העתקה 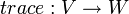 המגודרת
המגודרת 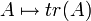 היא ה"ל.
היא ה"ל.
הוכחה: לכל 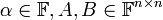

3. ![V=\mathbb{R}_{n}[x],\,W=\mathbb{R}_{n-1}[x]](/images/math/e/3/b/e3bb93e88ed069aa23de96c1fc0068e7.png) שניהם מעל
שניהם מעל 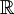 . אזי העתקה
. אזי העתקה 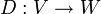 המגודרת
המגודרת 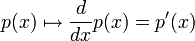 היא ה"ל.
היא ה"ל.
הוכחה:
![D[\alpha p_{1}(x)+p_{2}(x)]=[\alpha p_{1}(x)+p_{2}(x)]'=\alpha p_{1}'(x)+p_{2}'(x)=\alpha D[p_{1}(x)]+D[p_{2}(x)]](/images/math/2/1/2/212b3c164a73644cd93ef6149a1dd460.png)
4. העתקת הזהות 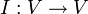 המוגדרת
המוגדרת 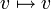 היא ה"ל.
היא ה"ל.
5. העתקת האפס 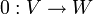 המוגדרת
המוגדרת 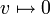 היא ה"ל.
היא ה"ל.
6. יהי  מ"ו מעל
מ"ו מעל 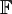 מימד
מימד  ויהי
ויהי  בסיס אזי הפונקציה
בסיס אזי הפונקציה 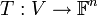 המוגדרת
המוגדרת ![v\mapsto [v]_B](/images/math/2/6/7/2670f477cf1b48d41e806ea128fae74d.png) היא ה"ל.
היא ה"ל.
תרגיל
יהיו 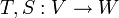 שתי ה"ל.
שתי ה"ל. 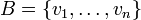 בסיס ל
בסיס ל  . נניח
. נניח  לכל
לכל 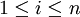
הוכח: 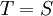 . כלומר לכל
. כלומר לכל 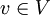 מתקיים
מתקיים 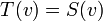
הוכחה: יהי 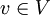 אזי
אזי 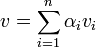 כי
כי  בסיס ובפרט פורשת.
ואז
בסיס ובפרט פורשת.
ואז
עיבוד הנוסחה נכשל (שגיאת תחביר): T(v)=T(\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots+\alpha_{n}v_{n})=\alpha_{1}T(v_{1})+\alpha_{2}T(v_{2})+\cdots+\alpha_{n}T(v_{n}) = \\ = \alpha_{1}S(v_{1})+\alpha_{2}S(v_{2})+\cdots+\alpha_{n}S(v_{n})=S(\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots+\alpha_{n}v_{n})=S(v)