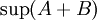הבדלים בין גרסאות בדף "משתמש:איתמר שטיין"

מתוך Math-Wiki

קפיצה אל: ניווט, חיפוש

גרסה מ־11:26, 28 בינואר 2013

הסבר על חישוב הופכי ב $\mathbb{Z}_p$

שאלה 1

סעיף ב

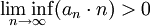
ידוע כי $\liminf_{n\rightarrow \infty}(a_n \cdot n)>0$

נניח ש

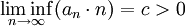
$\liminf_{n\rightarrow \infty}(a_n \cdot n)=c>0$

נסמן 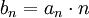$b_n=a_n\cdot n$

כלומר

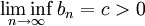
$\liminf_{n\rightarrow \infty}b_n=c>0$

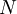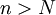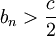
טענת עזר: קיים $N$ כך שאם $n>N$ אז $b_n>\frac{c}{2}$

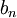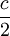(במילים אחרות: יש רק מספר סופי של איברים ב $b_n$ שיותר קטנים מ $\frac{c}{2}$ )

הוכחה: נניח בשלילה שזה לא נכון, כלומר קיימים אינסוף איברים מ 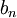$b_n$ שעבורם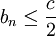 $b_n\leq \frac{c}{2}$

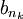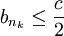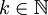
אז קיימת תת סדרה $b_{n_k}$ כך ש $b_{n_k}\leq \frac{c}{2}$ לכל $k\in \mathbb{N}$

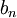נשים לב ש $b_n$ היא חסומה מלרע ולכן 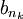$b_{n_k}$ חסומה גם מלעיל וגם מלרע.

לכן ל 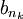$b_{n_k}$ יש תת סדרה מתכנסת 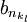$b_{n_{k_l}}$ כך ש

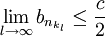
$\lim_{l\rightarrow\infty}b_{n_{k_l}}\leq \frac {c}{2}$

וזאת בסתירה לכך ש 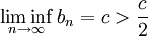$\liminf_{n\rightarrow \infty}b_n=c>\frac{c}{2}$

זה מוכיח את טענת העזר.

כעת, אנחנו יודעים שהחל מ 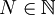$N\in \mathbb{N}$ כלשהוא מתקיים

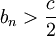
$b_n>\frac{c}{2}$

אבל בגלל ש 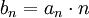$b_n=a_n\cdot n$ זה אומר שהחל מאותו 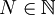$N\in \mathbb{N}$ מתקיים

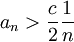
$a_n > \frac{c}{2} \frac{1}{n}$

בגלל שהטור 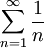$\ \sum_{n=1}^\infty \frac{1}{n}$ מתבדר

נובע ממבחן ההשוואה לטורים חיוביים שגם הטור 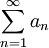$\ \sum_{n=1}^\infty a_n$ מתבדר.

שאלה 2

סעיף א

טענת עזר: אם 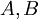$A,B$ קבוצות חסומות מלעיל אז

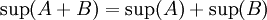
$\sup(A+B)=\sup(A)+\sup(B)$

הוכחה: נוכיח שהמספר 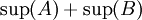$\sup(A)+\sup(B)$ מקיים את התכונות של $\sup(A+B)$

מקור: https://math-wiki.com/index.php?title=משתמש:איתמר_שטיין&oldid=31848