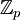משתמש:איתמר שטיין
הוכחה לטענה ש  הפיכה
הפיכה  ניתן להציג את
ניתן להציג את  כמכפלת מטריצות אלמנטריות.
כמכפלת מטריצות אלמנטריות.
שלב א':
כל מטריצה אלמנטרית היא הפיכה ומתקיים
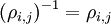
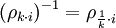
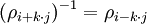
שלב ב': הוכחת 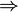 .
.
אם  היא מכפלה של מטריצות אלמנטריות אז היא מכפלה של מטריצות הפיכות ולכן הפיכה.
היא מכפלה של מטריצות אלמנטריות אז היא מכפלה של מטריצות הפיכות ולכן הפיכה.
שלב ג': מטריצה 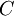 בעלת שורת אפסים היא לא הפיכה.
כי לכל מטריצה
בעלת שורת אפסים היא לא הפיכה.
כי לכל מטריצה  שהיא (נניח ש
שהיא (נניח ש 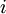 היא שורת האפסים)
היא שורת האפסים)
מתקיים לפי כפל שורה שורה 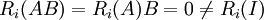 .
.
שלב ד': נתחיל להוכיח את 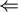 .
.
אם  הפיכה, הצורה המדורגת קנונית שלה היא
הפיכה, הצורה המדורגת קנונית שלה היא 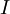 .
.
הסבר: נסמן את הצורה המדורגת קנונית של  ב
ב 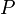 .
.
קיימות מטריצות אלמנטריות 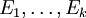 כך ש
כך ש
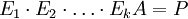 .
.
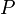 הפיכה כי היא מכפלה של מטריצות הפיכות.
הפיכה כי היא מכפלה של מטריצות הפיכות.
אבל לצורה מדורגת של מטריצה ריבועית יש רק 2 אפשרויות. או שהיא 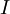 או שיש בה שורת אפסים.
או שיש בה שורת אפסים.
לכן 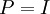 . (מטריצה בעלת שורת אפסים היא לא הפיכה).
. (מטריצה בעלת שורת אפסים היא לא הפיכה).
שלב ה: סיום
נותר רק לכפול משמאל את
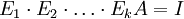 .
.
ב 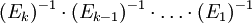 .
.
ולקבל
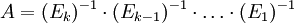
היות והופכי של מטריצה אלמנטרית הוא גם מטריצה אלמנטרית.
קיבלנו ש היא מכפלה של מטריצות אלמנטריות.--איתמר שטיין 20:44, 27 באוגוסט 2012 (IDT)
היא מכפלה של מטריצות אלמנטריות.--איתמר שטיין 20:44, 27 באוגוסט 2012 (IDT)